3.2. Présentation du composite
étudié
Dans le cadre de cette étude, nous utilisons un
matériau composite constitué d'une matrice polyester et
renforcé par des fibres de RC (Rhectophyllum Camerunense)
[12J. En effet, la matrice polyester est utilisé parce qu'elle
est disponible en quantité dans le marché local et les fibres de
RC parce qu'elles sont légères avec un grand module
d'Young [1J.
Tableau 3.1 : Tableau des
caractéristiques des constituants
Caractéristiques des constituants
|
Matrice Polyester
|
Fibres RC
|
[GPaJ
|
[GPaJ
|
|
[Kg/m3J
|
[GPaJ
|
[GPaJ
|
|
[Kg/m3J
|
2.8-3.6
|
1.40
|
0.4
|
1200
|
2.3-17
|
1.38-10.2
|
0.2
|
947
|
|
3.3. Programmation des équations de la
flèche sous Matlab
Dans cette simulation, nous nous intéressons aux
flèches maximales de la structure, pour cela, nous allons programmer
sous Matlab, l'équation de comportement de la flèche pour une
structure de type pli. Dans ce test il sera question d'évaluer pour un
élément, la :
· Variation de la flèche maximale en fonction des
dix premiers modes d'excitations ;
· Influence de la longueur de l'élément sur
le comportement de la flèche maximale ;
· Influence de la hauteur de l'élément sur le
comportement de la flèche maximale ;
· Influence du type de section de l'élément
sur le comportement de la flèche maximale ;
· Influence du taux sur le comportement de fibres de la
flèche maximale ;
· Influence du module d'Young sur le comportement de la
flèche maximale.
37
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
3.3.1. Présentation des éléments et
des conditions aux limites de la simulation
Dans cette simulation, nous utiliserons des
éléments de types poutre et plaque unidirectionnelle à
0°. Les conditions aux limites sont présentées dans le
tableau ci-dessous :
Tableau 3.2 : Présentation
des différentes conditions aux limites
|
Plaque
|
|
Plaque_AAAA
|
|
|
|
Poutres
|
|
Poutre_EE
|
|
|
|
|
Poutre_AA
|
|
|
|
|
Poutre_EL
|
|
|
|
3.3.2. Modélisation des éléments dans
le cas de l'élément poutre
3.3.2.1. Cas d'une poutre EE
Dans ce cas, les poutres simulées sont prismatiques de
dimensions 150x10x15 mm à section rectangulaire renforcées avec
un taux X?? = 60%.
a) Variation de la flèche maximale en fonction
des dix premiers modes d'excitations Présentation graphique des
résultats
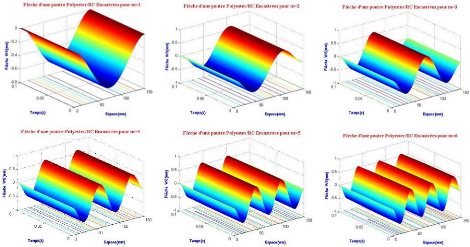
Figure 3.15 : Graphe de variation
de la flèche maximale pour les 6 premiers modes
38
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
Présentation numérique des
résultats
Ces résultats présentent les valeurs des
flèches maximales pour les différents modes. Tableau
3.3 : Valeurs des flèches maximales pour les 10
premiers modes d'une poutre EE
|
Flèche maximale d'une poutre composite
encastrée en Polyester/RC
|
|
X 1 = 35% ; ; ; :
rectangulaire ;150x15x15
|
|
Modes
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Flèche (mm)
|
0,5830
|
0,5540
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
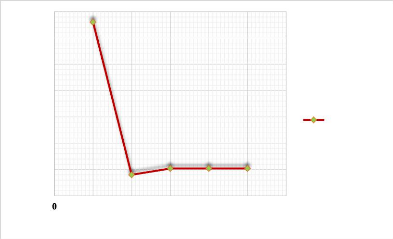
W0max (mm)
0,585
0,575
0,565
0,555
0,58
0,57
0,56
0,55
0,583
1 2 3 4 5 6
Mode "m"
0,554
0,5552
0,5552
0,5552
W0max=f(m)
Figure 3.16 : : Graphe de
variation de la flèche maximale en fonction des modes
Le mode fondamental 1, présente la flèche
maximale. Le mode 2 traduit le régime transitoire avec un pourcentage de
chute de 4.97% du mode 1 ; le mode 3 et les autres modes traduisent le
régime permanant avec un pourcentage d'élévation de 0,21%
par rapport au mode 2 et un écart relatif de 4,76% avec le mode
fondamental présenté comme le plus dangereux.
b) Influence de la longueur de la poutre sur le
comportement de la flèche maximale.
Dans ce test il est question de faire varier la longueur
« a » de la poutre, puis visualiser le comportement de la
flèche.
Tableau 3.4 : Valeurs des
flèches maximales avec différentes longueurs pour 5 modes d'une
poutre EE.
|
Poutre EE
|
Composite : Polyester/RC
|
Xf = 0.35
|
Ef = 8.5
|
|
Flèche maximale (mm)
|
q0 = 1N
|
h = 15
|
|
Modes
|
a = 80
|
a = 150
|
a = 250
|
a = 500
|
a = 750
|
a = 1000
|
Moyenne
|
Ecart type
|
|
1
|
1,0931
|
0,5830
|
0,3498
|
0,1749
|
0,1166
|
0,0874
|
0,41221667
|
0,39343837
|
|
2
|
1,0388
|
0,5540
|
0,3324
|
0,1662
|
0,1108
|
0,0831
|
0,39175
|
0,37389842
|
|
3
|
1,0411
|
0,5552
|
0,3331
|
0,1666
|
0.1110
|
0,0833
|
0,3926
|
0,37471908
|
|
4
|
1,0410
|
0,5552
|
0,3331
|
0,1666
|
0,1110
|
0,0833
|
0,39258333
|
0,37468447
|
|
5
|
1,0410
|
0,5552
|
0,3331
|
0,1666
|
0,1110
|
0,0833
|
0,39258333
|
0,37468447
|
39
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
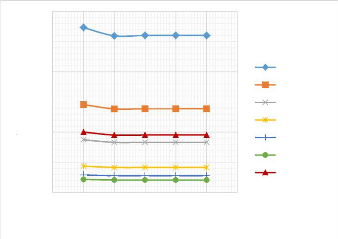
W0max (mm)
0,8
0,6
0,4
0,2
1,2
0
1
0 1 2 3 4 5 6
Mode "m"
a=80 mm a=150 mm a=250 mm a=500 mm a=750 mm a=1000 mm
Moyenne
Figure 3.17 : Influence de la
longueur de la poutre sur le comportement de la flèche
La flèche maximale croit avec la diminution de la
longueur de la poutre. Car la période des oscillations augmente avec la
longueur de la poutre. La figure ci-dessous présente une poutre de
longueur 1000 mm excitée au 5ème mode et le
tableau présente les valeurs des fréquences pour
différentes longueurs.
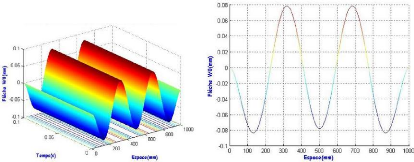
Figure 3.18 : Comportement de la
flèche sur une poutre EE de longueur 500 mm
Tableau 3.5 : Valeurs des
fréquences angulaires maximales avec différentes longueurs pour 5
modes d'une poutre EE.
|
Poutre
EE
|
Composite : Polyester/RC
|
Xf = 0.35
|
Ef = 8.5
|
|
Fréquence angulaire maximale
(Rad/s)
|
g0 = 1N
|
h = 15
|
|
Modes
|
a = 150
|
a = 250
|
a = 500
|
a = 750
|
a = 1000
|
Moyenne
|
Ecart type
|
|
1
|
124,8
|
44,9
|
11,2
|
5,00
|
2.80
|
37,74
|
51,5456
|
|
2
|
499
|
179,7
|
44,9
|
2,00
|
11,2
|
147,36
|
209,0835
|
|
3
|
1122,8
|
404,2
|
101,1
|
44,9
|
25,3
|
339,66
|
463,7052
|
|
4
|
1996,1
|
718,6
|
179,7
|
79,8
|
44,9
|
603,82
|
824,3913
|
|
5
|
3118,9
|
1122,8
|
280,7
|
124,8
|
70,2
|
943,48
|
1288,0936
|
40
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
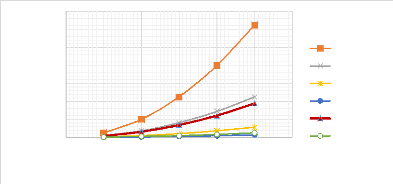
ù0max (rad/s)
3500
3000
2500
2000
1500
1000
500
0
0 1 2 3 4 5 6
Mode "m"
a=150 mm a=250 mm a=500 mm a=1000 mm Moyenne a=750
mm
Figure 3.19 : Influence de la
longueur de la poutre EE sur les fréquences angulaires propres Plus
une poutre est longue, moins elle vibre. Donc, les poutres
élancées ont tendance à absorber les vibrations.
c) Influence de la hauteur de la poutre sur le
comportement de la flèche maximale.
Dans ce test il est question de faire varier la hauteur totale
« h » de la poutre, puis visualiser le comportement de la
flèche.
Tableau 3.6 : Valeurs des
flèches maximales pour différentes hauteurs des 5 premiers modes
d'une poutre EE.
|
Poutre
EE
|
Composite : Polyester/RC
|
Xf = 0.35
|
Ef = 8.5
|
|
Flèche maximale (mm)
|
g0 = 1N
|
a = 150
|
|
Modes
|
h = 10
|
h = 15
|
h = 20
|
h = 25
|
h = 30
|
Moyenne
|
Ecart type
|
|
1
|
1,9676
|
0,5830
|
0,2459
|
0,1259
|
0,0729
|
0,59906
|
0,79035
|
|
2
|
1,8698
|
0,5540
|
0,2337
|
0,1197
|
0,0693
|
0,5693
|
0,75105
|
|
3
|
1,8739
|
0,5552
|
0,2342
|
0,1199
|
0,0694
|
0,57052
|
0,75272
|
|
4
|
1,8738
|
0,5552
|
0,2342
|
0,1199
|
0,0694
|
0,5705
|
0,75267
|
|
5
|
1,8738
|
0,5552
|
0,2342
|
0,1199
|
0,0694
|
0,5705
|
0,75267
|
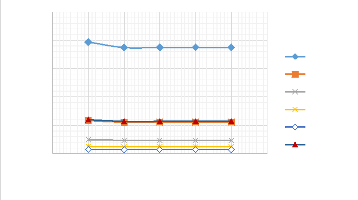
W0max (mm)
2,5
0,5
1,5
2
0
1
0 1 2 3 4 5 6
Mode "m"
h=10 mm h=15 mm h=20 mm h=25 mm h=30 mm
Moyenne
Figure 3.20 : Influence de la
hauteur de la poutre (EE) sur le comportement de la flèche.
41
|
|



