Chapitre 3 : Simulation numérique du
comportement vibratoire d'une structure composite
Lorsque la hauteur d'une poutre est grande, la structure
devient de plus en plus rigide et provoque ainsi une diminution de la
flèche maximale. La figure ci-dessous présente une poutre de
hauteur 15 mm excitée au mode 5.
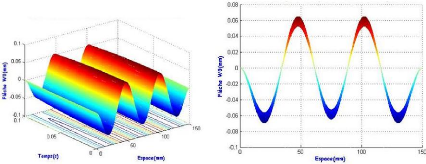
Figure 3.21 : Influence de la
hauteur de la poutre (EE) sur les caractéristiques vibratoires.
Tableau 3.7 : Valeurs des
fréquences maximales pour différentes hauteurs des 5 premiers
modes d'une poutre EE.
|
Poutre
EE
|
Composite : Polyester/RC
|
Xf = 0.35
|
Ef = 8.55
|
|
Fréquence angulaire maximale
(Rad/s)
|
g0 = 1N
|
a = 150
|
|
Modes
|
h = 8
|
h = 10
|
h = 12
|
h = 15
|
Moyenne
|
Ecart type
|
|
1
|
66,5
|
83,2
|
99,8
|
124,8
|
93,575
|
24,86260579
|
|
2
|
266,1
|
332,7
|
399,2
|
499
|
374,25
|
99,34433384
|
|
3
|
598,8
|
748,5
|
898,2
|
1122,8
|
842,075
|
223,5289299
|
|
4
|
1064,6
|
1330,7
|
1596,9
|
1996,1
|
1497,075
|
397,3689501
|
|
5
|
1663,4
|
2079,3
|
2495,2
|
3118,9
|
2339,2
|
620,8922988
|
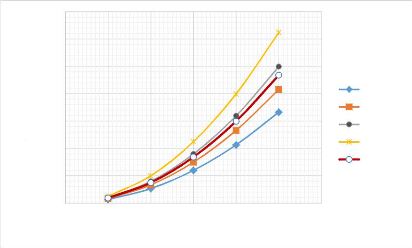
ù0max (rad/s)
3500
3000
2500
2000
1500
1000
500
0
0 1 2 3 4 5 6
Mode "m"
h=8 mm h=10 mm h=12 mm h=15 mm
Moyenne
Figure 3.22 : Influence de la
hauteur de la poutre (EE) sur les fréquences angulaires.
42
Chapitre 3 : Simulation numérique du
comportement vibratoire d'une structure composite
La fréquence angulaire croit avec l'augmentation de
hauteur de la poutre. Plus une poutre est rigide et plus elle est sensible aux
vibrations transversales.
d) Influence du type section d'une poutre sur le
comportement de la flèche maximale.
Dans ce test, il est question d'analyser l'influence du type
de section sur le comportement de la flèche d'une poutre. Pour y
parvenir, nous modifierons l'expression du moment quadratique « 4 »
caractérisant le type de section.
Tableau 3.8 : Valeurs des
flèches maximales pour différents types de sections d'une poutre
EE suivant les 5 premiers modes d'excitations.
|
Xf= 0.35
|
Ef= 8.5
|
|
|
q0= 1N
|
a= 150
|
|
Poutre EE
|
Composite : Polyester/RC
|
|
Flèche maximale (mm)
|
|
S_Rect.-P
|
S_Rect.C
|
S_Cir.-P
|
S_Cir.C
|
S_Car. -P
|
S_Car.C
|
|
Modes
|
|
1
|
0,5830
|
0,5830
|
0,5830
|
0,5830
|
0,5830
|
0,5830
|
|
2
|
0,5540
|
0,5540
|
0,5540
|
0,5540
|
0,5540
|
0,5540
|
|
3
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
|
4
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
|
5
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
0,5552
|
Pour des poutres de section rectangulaire, carrée et
circulaire, soumises à des vibrations, la valeur de la flèche
maximale d'une poutre encastrée à ses deux
extrémités n'a pas d'influence sur le comportement de la
flèche. Donc la flèche d'une structure composite est liée
aux caractéristiques des constituants. Néanmoins, nous observons
une modification de la période d'oscillation.
Tableau 3.9 : Valeurs des
fréquences maximales pour différents types de section d'une
poutre EE suivant les 5 premiers modes d'excitations.
|
Poutre EE
|
Composite : Polyester/RC
|
|
Fréquence angulaire maximale
(Rad/s)
|
|
Modes
|
S_Rect.-P
|
S_Rect.C
|
S_Cir.-P
|
S_Cir.C
|
S_Car. -P
|
S_Car. -C
|
|
1
|
112,352
|
99,4807
|
86,2296
|
80,4481
|
79,4449
|
74,1183
|
|
2
|
312,0889
|
276,3353
|
239,5267
|
223,467
|
220,6802
|
205,8841
|
|
3
|
611,6943
|
541,6172
|
469,4723
|
437,9953
|
432,5332
|
403,5328
|
|
4
|
1011,2
|
895,3264
|
776,0665
|
724,033
|
715,0038
|
667,0645
|
|
5
|
1,51E+03
|
1337,5
|
1159,3
|
1081,6
|
1068,1
|
996,479
|
|
Moyenne
|
711,5675
|
630,052
|
546,112
|
509,5087
|
503,1525
|
469,416
|
|
Ecart type
|
560,5109
|
496,3102
|
430,1856
|
401,3528
|
396,3435
|
369,767
|
43
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
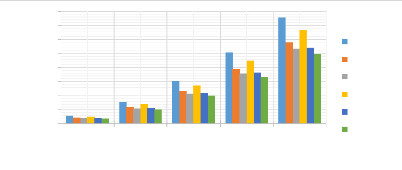
ù0max (rad/s)
1600
1400
1200
1000
800
600
400
200
0
1 2 3 4 5
Modes "m"
S_Rect.-P S_Cir.-P S_Car. -P S_Rect.C S_Cir.C
S_Car.C
Figure 3.23 : Influence du type de
section d'une poutre (EE) sur les fréquences angulaires.
Donc, les poutres à sections rectangulaires ont des
fréquences angulaires plus importantes que les autres sections, tandis
que les poutres à sections carrées ont des fréquences
propres moins élevées. e) Influence du taux de fibres
sur le comportement de la flèche maximale.
Dans ce test, il est question de faire varier le taux de
fibres d'une poutre et observer le comportement de la flèche.
Tableau 3.10 : Valeurs des
flèches maximales pour différents taux de fibres d'une poutre EE
suivant les 5 premiers modes d'excitations.
|
Poutre EE
|
Composite : Polyester/RC
|
a = 150
|
|
Flèche maximale (mm)
|
Ef = 8.5
|
|
Modes
|
Xf= 0.25
|
Xf= 0.35
|
Xf= 0.50
|
Xf= 0.60
|
Moyenne mi
|
|
1
|
0,6515
|
0,5830
|
0,5053
|
0,4648
|
0,55115
|
|
2
|
0,6192
|
0,5540
|
0,4802
|
0,4417
|
0,523775
|
|
3
|
0,6205
|
0,5552
|
0,4812
|
0,4427
|
0,5249
|
|
4
|
0,6205
|
0,5552
|
0,4812
|
0,4426
|
0,524875
|
|
5
|
0,6205
|
0,5552
|
0,4812
|
0,4426
|
0,524875
|
|
Moyenne Xi
|
0,62644
|
0,56052
|
0,48582
|
0,44688
|
|
|
Ecart type
|
0,0141
|
0,0126
|
0,011
|
0,010026
|
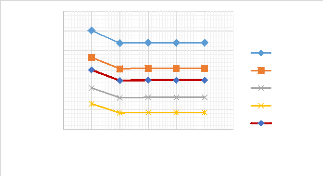
w0max (mm
0,65
0,55
0,45
0,7
0,6
0,5
0,4
0 1 2 3 4 5 6
Modes "m"
Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60
Moyenne
Figure 3.24 : Influence du taux
de fibres sur le comportement de la flèche d'une poutre (EE).
44
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
Plus le taux de fibres est important dans une poutre moins la
flèche est importante. Mais, nous observons une modification de la
période d'oscillation. Donc, le taux de fibres est responsable de la
diminution de la flèche.
Tableau 3.11 : Valeurs des
fréquences maximales pour différents taux de fibres d'une poutre
EE suivant les 5 premiers modes d'excitations.
|
Poutre EE
|
Composite : Polyester/RC
|
|
Fréquence angulaire maximale
(Rad/s)
|
|
Modes
|
???? = ??.????
|
???? = ??.????
|
???? = ??.????
|
???? = ??.????
|
|
1
|
115,8
|
124,8
|
137,8
|
146,3
|
|
2
|
463,2
|
499
|
551,18
|
585,3
|
|
3
|
1042,2
|
1122,8
|
1240,2
|
1316,8
|
|
4
|
1852,8
|
1996,1
|
2204,8
|
2341,1
|
|
5
|
2894,9
|
3118,9
|
3444,9
|
3657,9
|
|
Moyenne
|
1273,78
|
1372,32
|
1515,776
|
1609,48
|
|
Ecart type
|
1119,697
|
1206,327
|
1332,43
|
1414,814
|
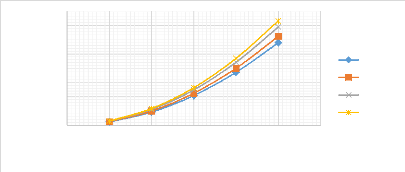
ù0max (rad/s)
4000,4
3500,4
3000,4
2500,4
2000,4
1500,4
1000,4
500,4
0,4
0 1 2 3 4 5 6
Modes "m"
Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60
Figure 3.25 : Influence du taux de
fibres sur les fréquences angulaires dans une poutre (EE)
Les graphes des figures (3.12 et 3.13) montrent que plus le
taux de fibres est important dans une poutre (EE), plus la fréquence
angulaire est aussi importante.
f) Influence du module d'Young des fibres sur le
comportement de la flèche maximale. Dans ce test, il est
question de faire varier le taux de fibres d'une poutre et observer le
comportement de la flèche.
Tableau 3.12 : Valeurs des
flèches maximales pour différents modules d'Young d'une poutre EE
suivant les 5 premiers modes d'excitations.
|
Poutre
EE
|
Composite : Polyester/RC
|
?? = ??????
|
???? = ??.????
|
|
Flèche maximale (mm)
|
?????????? = ??.??
|
?????????? = ????
|
|
Modes
|
??????????
|
??/????????
|
???? = ??????
|
??/????????
|
??????????
|
Moyenne
|
Ecart type
|
|
1
|
1,0649
|
0,9946
|
0,5830
|
0,445
|
0,3598
|
0,68946
|
0,32165033
|
|
2
|
1,0120
|
0,9452
|
0,5540
|
0,4228
|
0,3419
|
0,65518
|
0,30570179
|
|
3
|
1,0142
|
0,9473
|
0,5552
|
0,4238
|
0,3426
|
0,65662
|
0,30637316
|
|
4
|
1,0141
|
0,9472
|
0,5552
|
0,4237
|
0,3426
|
0,65656
|
0,30633926
|
|
5
|
1,0141
|
0,9472
|
0,5552
|
0,4237
|
0,3426
|
0,65656
|
0,30633926
|
45
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
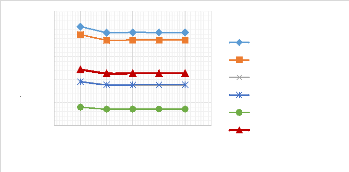
w0max (mm)
0,8
0,6
0,4
0,2
1,2
1
0 1 2 3 4 5 6
Modes "m"
Ef=Efmin=2,3 Ef=1/3Efmoy=2,83 Ef=Efmoy=8,5
Ef=3/2Efmoy=12,75 Ef=Efmax=17 Moyenne
Figure 3.26 : Influence du module
d'Young des fibres sur le comportement de la flèche de la poutre (EE).
Plus le module d'Young de fibres est important dans une poutre moins la
flèche est importante. Donc plus les fibres sont résistantes,
plus la structure est rigide et plus la flèche est réduite. Ceci
s'accorde avec les résultats obtenus lorsque nous faisions varier la
hauteur.
Tableau 3.13 : Valeurs des
fréquences maximales pour différents modules d'Young des fibres
d'une poutre EE suivant les 5 premiers modes d'excitations.
|
Poutre
EE
|
Composite : Polyester/RC
|
a = 150
|
Xf = 0.35
|
|
Flèche maximale (mm)
|
Ef = 8.5
|
Ef = 8.5
|
|
Modes
|
Efmin
|
1/3Ef m
|
Ef = Ef m
|
3/2Efm
|
Efma
|
Moyenne
|
Ecart type
|
|
1
|
92,3
|
95,5
|
124,8
|
142,8
|
158,8
|
122,84
|
29,0496
|
|
2
|
369,2
|
382,1
|
499
|
571,2
|
635,2
|
491,34
|
116,1718
|
|
3
|
830,8
|
859,6
|
1122,8
|
1285,2
|
1429,3
|
1105,54
|
261,4214
|
|
4
|
1479,6
|
1528,2
|
1996,1
|
2284,9
|
2541
|
1965,96
|
464,0802
|
|
5
|
2307,7
|
2387,8
|
3118,9
|
3570,1
|
3970,3
|
3070,96
|
726,2101
|
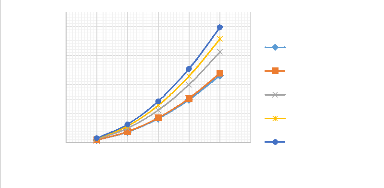
ù0max (rad/s)
2500,4
2000,4
4500,4
4000,4
3500,4
3000,4
1500,4
1000,4
500,4
0,4
0 1 2 3 4 5 6
Modes "m"
Ef=Efmin=2,3 Ef=1/3Efmoy=2,83 Ef=Efmoy=8,5
Ef=3/2Efmoy=12,75 Ef=Efmax=17
Figure 3.27 : Influence du taux
de fibres sur les fréquences angulaires dans une poutre (EE)
Les graphes des figures (3.12 et 3.13) montrent que plus le
module d'Young des fibres est important dans une poutre (EE), plus la
fréquence angulaire est aussi importante. Donc, la fréquence
angulaire varie avec la résistance des fibres.
46
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
3.3.2.2. Cas d'une poutre EL
Dans ce cas, les poutres simulées sont prismatiques de
dimensions 150x15x15 mm à section rectangulaire renforcées avec
un taux X f = 35%.
a) Variation de la flèche maximale en fonction
des dix premiers modes d'excitations Présentation graphique des
résultats
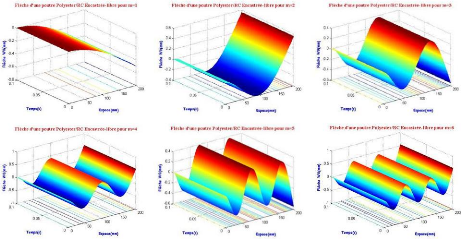
Figure 3.28 : Comportement de la
flèche pour les 6 premiers modes d'une poutre EL
Présentation numérique des
résultats
Ces résultats présentent les valeurs des
flèches maximales pour les différents modes. Tableau
3.14 : Valeurs des flèches maximales pour les 10
premiers modes d'une poutre EL
|
Flèche maximale d'une poutre composite
encastrée en Polyester/RC
|
|
X f = 35% ; ; ; :
rectangulaire ;150x15x15
|
|
Modes
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Flèche
(mm)
|
0,5050
|
0,5505
|
0,5506
|
0,5506
|
0,5506
|
0,5506
|
0,5506
|
0,5506
|
0,5506
|
0,5506
|
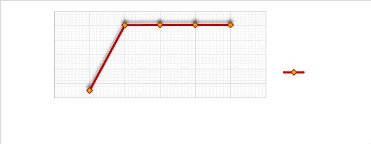
Pour une poutre encastrée-libre, la flèche croit et
converge pour les 3 premiers modes et devient constante jusqu'au
10ème mode.
W0max (mm)
0,56
0,55
0,54
0,53
0,52
0,51
0,5
0 1 2 3 4 5 6
0,505
0,5505 0,5506 0,5506 0,5506
Modes "m"
Flèche (mm)
Figure 3.29 : Graphe de variation
de la flèche maximale en fonction des modes
47
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
Le mode fondamental 1 est le moins influent car,
présente la flèche minimale. Le mode 2 traduit le régime
transitoire avec un pourcentage d'élévation de 8,2% du mode 1 ;
le mode 3 et les autres modes traduisent le régime permanant avec un
pourcentage d'élévation de 0,02% par rapport au mode 2 et un
écart relatif de 9,03% avec le mode fondamental présenté
comme le plus dangereux.
Influence du taux de fibres sur le comportement de la
flèche maximale.
Dans ce test, il est question de faire varier le taux de
fibres d'une poutre et observer le comportement de la flèche.
Tableau 3.15 : Valeurs des
flèches maximales pour différents taux de fibres d'une poutre EL
suivant les 5 premiers modes d'excitations.
|
Poutre EL
|
Composite : Polyester/RC
|
a = 150
|
|
Flèche maximale (mm)
|
Ef = 8.5
|
|
Modes
|
Xf= 0.25
|
Xf= 0.35
|
Xf= 0.50
|
Xf= 0.60
|
Moyenne mi
|
|
1
|
0,5644
|
0,5050
|
0,4377
|
0,4026
|
0,477425
|
|
2
|
0,6153
|
0,5505
|
0,4771
|
0,4389
|
0,52045
|
|
3
|
0,6154
|
0,5506
|
0,4472
|
0,4390
|
0,52055
|
|
4
|
0,6154
|
0,5506
|
0,4472
|
0,4390
|
0,52055
|
|
5
|
0,6154
|
0,5506
|
0,4472
|
0,4390
|
0,52055
|
w0max (mm)
0,65
0,55
0,45
0,6
0,5
0,4
0 1 2 3 4 5 6
Modes "m"
Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60
Moyenne
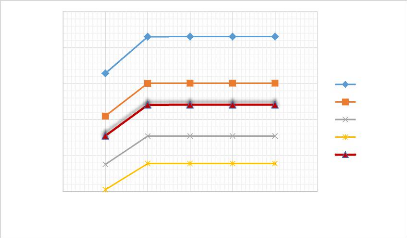
Figure 3.30 : Influence du taux
de fibres sur le comportement de la flèche d'une poutre (EL).
Donc, plus le taux de fibres est important dans une poutre EL
moins la flèche est importante. Les figures ci-dessus montrent une
poutre EL à section rectangulaire de longueur « a=200, h=15, »
excitée au mode 5 renforcé avec un taux de fibres > 35%.
48
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
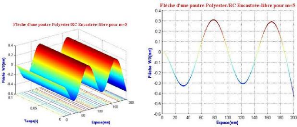
Figure 3.31 : Influence un
taux de fibres > 35% de la poutre (EL) sur les caractéristiques
vibratoires.
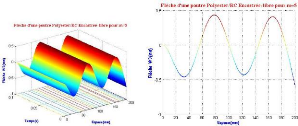
Figure 3.32 : Influence un
taux de fibres < 35% de la poutre (EL) sur les caractéristiques
vibratoires. Du point de vue cinématique, la poutre EL a plus de
degrés de libertés que la poutre EE. Donc lorsqu'on structure
possède moins de degrés de libertés, le mode fondamental
n'est plus critique.
|
|



