33
Où les valeurs des coefficients C1, C2 et C3 sont
fonctions des conditions aux appuis. [Annexe 1]. 2.3.4. Cas d'une plaque
orthotrope à côtés encastrés (EEEE)
cos ? i ? cosh ? i
? ?
i sin ? ? sinh
? i
i
m n
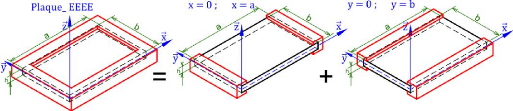
Figure 2.13 : Plaque rectangulaire
encastrée sur ses 4 côtés (EEEE) Par analogie au cas
d'une poutre encastrée à ses deux extrémités, nous
avons pour :
?
?
|
Les côtés X = 0 et X = a
encastrés :
Les côtés y = 0 et y = b
encastrés, nous avons :
Où : Et
|
|
(2.135)
(2.136)
(2.137) (2.138a)
(2.138b)
(2.139)
|
|
|
)
2.3.1. Cas d'une plaque orthotrope à deux
côtés opposés encastrés et les deux autres en appuis
simples (AEAE)

Figure 2.14 : Plaque
encastrée sur 2 côtés consécutifs et en appui simple
sur les 2 autres (AEAE). Par analogie au cas d'une poutre encastrée
à ses deux extrémités, nous avons pour :
? Les côtés X = 0 et X = a en
appuis simples, nous avons :
Chapitre 2 : Formulation théorique de
l'équation de comportement de la flèche en vibration de flexion
d'un composite
|
|
|
(2.83)
|
|
|
Les côtés y = 0 et y = b encastrés, nous
avons :
|
|
|
|
|
(2.84)
|
|
|
|
(2.138)
|
|
;
|
|
Donc :
|
|
|
|
Parvenue au terme de ce chapitre portant sur le calcul
vibratoire en flexion d'un matériau composite, il est important de
constater que l'objectif de la détermination des équations de
comportement de la flèche a été atteint au moyen de la
formulation de la théorie classique des stratifiés basée
elle-même sur le modèle cinématique d'une plaque de
Love-Kirchhoff. Cette théorie classique nous a permis de déduire
l'équation de comportement de mouvement correspondant au mouvement
transverse pour le cas d'une structure stratifié unidirectionnelle ou
orthotrope sollicitée en flexion. L'extension de cette théorie
sur la théorie des poutres nous a permis de ressortir l'équation
des vibrations transverses d'une poutre. La solution de ces équations
obtenue par la méthode de séparation des variables exprime la
flèche recherchée en fonction de la déformée
modale, de la fréquence angulaire et du temps. En considérant les
différentes conditions aux extrémités, la condition de
stationnarité5 et en tenant compte de la fonction
d'énergie comme l'impose la méthode de Rayleigh-Ritz, nous avons
ressortie l'expression explicite de la
fréquence propre pour un mode d'excitation. Cependant,
l'effort de calcul au moyen d'une méthode
analytique manuelle est
très important et prend beaucoup trop de temps. Raison pour laquelle, il
sera question par la suite, d'implémenter ses équations dans le
logiciel Matlab pour effectuer une simulation du comportement de la
flèche.
34
5 Stationnarité : identifié ici par un flambement
statique ou une flexion statique.
CHAPITRE 3 : SIMULATION NUMERIQUE SOUS MATLAB DU
COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE.
| 


