Chapitre 1 : Etat de l'art sur le comportement
vibratoire d'un matériau composite
1.4.1. Les différents paramètres de la
flexion pure d'une plaque orthotrope
Considérons une structure composite orthotrope soumise
à un chargement transverse q (x, y) et configuré comme
le montre la figure ci-dessous.
??divN ?
? 2 2 2
u ? u ?
v
0 0 0
A ? A 2 ( 12
? A ? A 66 ) ?
0
11 2 66
? x ? y ? x
? y
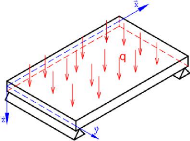
Figure 1.6 : Schémas d'une
plaque pour flexion cylindrique.
Le comportement statique d'une telle structure est
caractérisée par l'équation d'équilibre :
(1.39)
a 2 2 2
u a v a v
0 0 0
( 12
A + A 66 ) + A A
= 0
66 2 22 2
a x a y a x a y
e 4 4 4
w e w e w
0 0 0
D + 2( 2 ) 2
2
11 4 12 + =
66 22 4
e x e x e y e y
En l'absence des forces de volumes , il vient :
? divM ???
D D + D q
En développant l'équation constitutive, puis en
reportant le résultat dans (a), il vient en l'absence des charges
axiales :
? ?
w ( x , y
) = ?? C k
k=1 l=1
(1.40)
(1.41)
x y
qkl ? 0
(1.42)
En flexion pure, l'équation d'équilibre est
réduite à l'équation (1.42), donc la solution
recherchée
pour une plaque en appuis simples est de la forme :
16 q 0
kl kl? 2
(1.43)
qkl
?
Avec :
Ckl
?
2
(1.44)
4 2 2 4
? ?
k
? ? ? 2 ? ?
11 12 ? ? ? ? ? ? ? ?
? ? ? ? ? ?
k l l
D D 2 D D
66 22
? ?
a ? ? ? ? ? ?
a b a
12
|
q?
Et :
|
, si et sont impairs ; (1.45)
|
, si et sont pairs.
Le comportement de la flèche en un point M (x, y)
de la plaque s'écrit :
13
| 


