Chapitre 1 : Etat de l'art sur le comportement
vibratoire d'un matériau composite
(1.46)
Avec : (1.47)
a 2 2 3
U a V a W
0 0 0
A ? A ? B -
0
Et : (1.48)
11 2 16 2 12 3
a x ax ax
1.4.2. Les différents paramètres de la
flexion cylindrique d'une structure orthotrope
En flexion cylindrique, la déformation de la plaque est
considérée comme indépendante de la coordonnée
suivant la longueur de la plaque.
Configuration de la plaque en flexion
cylindrique
Considérons une plaque stratifiée à n
couches très longue suivant y, soumise à une charge
transversale ??, configurée comme le montre la figure ci-dessous.
a 2 2 3
u a v a w
0 0 0
A ? A ? B =
0
16 2 66 2 16 3
a x a x ax
a 4 3 3
w a u a v
0 0 0
D -- B -- B =
q
11 4 11 3 16 3
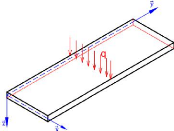
Figure 1.7 : Schémas d'une
plaque pour flexion cylindrique. Les équations d'équilibres
en l'absence des charges axiales sont dans cas :
a x a x a x
0( ) m cos
w 0( x )
0( ) m cos
|
u x A
? m ?
0( ) m cos
v x B
? m ?
|
(1.49)
(1.50)
|
x
(1.51)
Pour une poutre en appuis simples, les solutions
générales de cette équation sont de la forme :
(1.52)
w x C
? m ?
a
x
a
x
a
(1.53)
(1.54)
Où est la flèche recherchée, ?? est la
fréquence angulaire et est la déformée modale.
En flexion pure, il vient :
?
w 1
0 ?
q
x D
? 11
4 4 (1.55)
14
| 


