étude du comportement de la flèche d’un matériau composite en vibration et simulation sous Matlab.

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

(1.4)

^Q = C4Q11 + _S4Q22 + ^2C2S2

¹¹

^Q2'2= S4Q11 + _C4Q22 + ^2S2C2

^Q

^_C2S2 66 - ^{Q12 =Q12(C4+S4)+(Q11+Q22-4Q66)C2S2}

Q;6=C3S( ^{-Q11+Q12+ 2Q66)+S3C(Q22-Q21-2Q66)} Q26 = S3C( ^-Q11 + ^Q12 + ^{2Q66)+ C3S(Q22 -Q21 -2Q66) (Q12 +2Q66)}

^{(Q12 +2Q66)}

( Q ^{11+Q 22-2Q} 12 -2Q ⁶⁶⁾⁺ Q ⁶ 6 (C ⁴ +S4)

Où : etS=Sin8

1.3. Formulation de la théorie classique des stratifiées

La théorie classique des stratifié nous permet d'établir les équations de mouvement d'une structure stratifié en se basant sur le modèle de Love-Kirchhoff ou de Mindlin. Mindlin dans sa théorie prend en compte le cisaillement transverse en supposant qu'une section effectue une rotation par rapport au plan moyen de la plaque tandis que Love-Kirchhoff rejoignent le modèle des plaques de Euler-Bernoulli qui ne tienne pas compte du cisaillement transverse. Ce dernier modèle sera retenu pour la suite de notre travail.

1.3.1. Hypothèses de Love-Kirchhoff

Le modèle de Love-Kirchhoff considère que [2] :

- La plaque est mince et L/h > 20 ;

- Les déformations et les déplacements restent petits (Hypothèse des petites perturbations) ; - Les interfaces entre les plis sont parfaites· ;

- Au cours de la déformation, les segments restent perpendiculaires à la surface moyenne, ce

qui permet de négliger l'effet du cisaillement transverse .

6

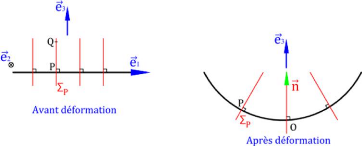
Figure 1.3 : Schématisation d'une plaque selon Love-Kirchhoff [2] 1.3.2. Expression du champ de déplacement cinématiquement admissible

Le champ général de déplacement en un point M d'une plaque de Love-Kirchhoff à l'instant t, s'exprime par :

7