étude du comportement de la flèche d’un matériau composite en vibration et simulation sous Matlab.

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

_{v w} w 0

ÇO y

2 ? _{ö ö} ) ? _ö )

_{z y 2 y}

(1.5)

Où : et sont des déplacements membranaires dans les directions L et T ; et sont des

rotations dues à la flexion ; est la flèche de la plaque.

1.3.3. Expression générale du champ de déformation Le champ de déformation s'exprime par :

e yz = I + 1 = I + I

? ? ?

? ?

_{x y}

_{a w}

- ? -

? ₉

_{y x}

_{a y}

	·	(1.6)

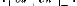
(1.7)

(1.8)

(1.9)

(1.10)

(1.11)

Dans les conditions de Bernoulli-Euler qui ne tiennent pas compte du cisaillement transverse,

nous avons : . (1.12)
En reportant (1.12) dans (1.11) et (1.10), nous avons :

?w 0 ?x	0 (1.13)
En tenant compte de (1.13), (1.5), devient : ? ^wu x y t u x y tz x ^0 ( , , ) ( , , ) ? -- S = 0 S ^w ? ? ? ^v x y t v x y tz y ^0 ( , , ) = ( , , ) -- S S ^0 ? ? ^w( ^x, ^y, ^t) = w 0 ( ^x, ^y, ^t) ? ? En un point ??, le tenseur de déformation se traduit par l'expression : ? ? ? 0 ? ? ? ? xx xy xx ? ? ? ? ? ? ? ? ? 0 xy yy ? ? ? ? ? yy ? ? 0 0 0???? ? ? ? xy En tenant compte de (1.19), le tenseur de déformation peut se décomposer par :		(1.14) (1.15)

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

(1.16)

Il en ressort deux tenseurs des déformations représentant chacun :

n Le tenseur des déformations en membrane :

(1.17)

?? ?

^u0

? ?

?

? ? ? ? ?

^xx v

^{0 0}

^?m ? ^?yy ?

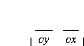
?0??

?

0??v

y

u

0

?? ? ? ?

^{0 x}

n Le tenseur des déformations en flexion et torsion :

^yy

^?f

??

(1.18)

? ? ? ?

y x ?? ? ^2w0 ? ? z?x2 ^{kxx ?z?k? ????z?2w0} ?y2 k ?????xy 2z ?2w0 ^?x?y

8

En posant 6 _f = zk , nous avons la matrice des courbures k . (1.19)

Finalement, le tenseur des déformations s'écrit :

(1.20)

1.3.4. Expression du champ de contraintes

En considérant (2.11), pour un pli k de normale ?? soumis à un état de contraintes planes, la loi de Hooke sur les axes du matériau s'écrit :

''

? ? ?

? _{Q Q Q}

' ? ? ?

?

' ' (1.23)

16 11 12 xx ? ? ? xx ? ? ? ' ' ' ? ? ? ? ? Q Q Q ? yy 12 26 ? ? yy ? 22 ? ? ? ' ' ' ? ? ? ? ? ? ? ? Q Q Q xy 16 26 ? ? ? ? ?xy k k 66 k ? ? Q ?m ? zQ k En tenant compte de (2.23), (2.24) devient : ' ' ' ' ? ? ? ? Q Q Q ? ? ? ? ?0 Q Q Q k ' ' ? ? ? xx 16 16 11 12 11 12 xx ? ? ? ? xx ? ? ? ? ? ? ' ' ' ? ? ? ? 0 ' ' ' ? ? Q Q Q z Q Q Q k 12 26 ? ? ? ? ? yy yy 12 26 ? ? ? yy 22 22 ? ? ? ? ? ? ? ? ' ' ' 0 ' ' ' ? ? ? ? ?xy 16 26 16 26 ? ? ? ? ? ? xy xy ? ? Q Q Q ? Q Q Q k ? ? ? ? k 66 k k k 66 k

(1.21) (1.22)