1.8.2- Remboursement à capital constant
Cette méthode est rarement choisie par les emprunteurs,
elle consiste à un remboursement par amortissement du capital constant
et un remboursement d'intérêts dégressif. Ce qui donne une
mensualité dégressive. Pour mieux comprendre cette méthode
nous allons prendre un exemple.
Exemple
On reprend l'exemple précédent, mais avec un
remboursement à capital constant.
o Pour la première mensualité
Capital = 2 000 000 / 360 = 5 555.55 DA Intérêt
= 2 000 000 * 0.005 = 10 000 DA Mensualité = 15 555.55 DA
o Pour la deuxième mensualité Capital = 5 555.55
DA
Intérêt = 1 994 444.45 * 0.005 = 9 972.22 DA
Mensualité = 15 527.72 DA
o Pour la troisième mensualité
Capital = 5 555.55 DA
Intérêt = 1 988 888.90 * 0.005 = 9 944.44 DA
Mensualité = 15 499.9945
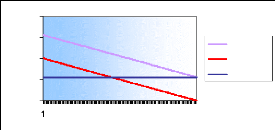
Nous avons étudié l'évolution des
intérêts du capital et des échéances sur 360 mois et
cela nous a permis d'élaborer le graphique suivant :
20000
15000
10000
5000
0
45 89 133 177 221 265 309 353
Échéance Intérêt Capital
82
Graphe représentant l'évolution du
remboursement des intérêts et des mensualités pour un
remboursement du capital constant
Quatrième partie Cas pratiques
83
Ce graphe nous montre que le remboursement des
intérêts est dégressif ce qui nous donne des
mensualités dégressives ce qui ne correspond pas à la
situation financière du ménage qu'a tendance à
s'améliorer dans le futur (augmentation de salaire).Ce qui explique la
faible demande sur cette modalité de remboursement, malgré son
coût global, moins chere comme vous pouvez le constater sur le tableau
ci-dessous.
Si on reprend notre exemple précédent :
|
Rubriques
|
Echéances constantes
|
Capital constant
|
|
Total Echéances
|
4
|
316 763.781 DA
|
3
|
805
|
000 DA
|
|
Principal
|
|
2 000 000 DA
|
2
|
000
|
000 DA
|
|
Total Intérêts
|
2
|
316 763.781 DA
|
1
|
805
|
000 DA
|
| 


