1.6- Taux d'intérêt
Il diffère selon le type de livret épargne ouvert
et selon la qualité d'épargnant ou non de l'emprunteur :
É Pour les titulaires d'un Livret Epargne Logement (LEL)
et / ou de Compte de Placement à Terme (CPT) le taux est de 6% l'an ;
É Pour les titulaires d'un Livret Epargne Populaire
(LEP), le taux est de 7% ;
Remarque
Pour avoir la qualité d'épargnant, le livret
épargne doit avoir au moins trois (03) ans d'ancienneté, et avoir
produit au moins 2500 DA d'intérêts.
É Pour les non épargnant le taux est de 7.25%.
1.7- Commissions
C'est l'ensemble des frais d'études et de gestion du
crédit qui sont payées en une seule fois par un
prélèvement sur le premier décaissement du crédit
octroyé.
Ces commissions sont fixes et sont en fonction du montant du
crédit comme suit :
Montant du crédit
|
Commissions d'études et de gestion
|
Jusqu'à 500 000 DA
|
1000 DA
|
De 500 000 DA à 2 000 000 DA
|
1500 DA
|
Supérieur à 2 000 0000 DA
|
2500 DA
|
|
Il y aussi la commission d'engagement qui est fixée
à 0.1% sur le montant non encore mobilisée. Elle
représente les frais d'immobilisation de fonds perçue lors du
décaissement des tranches de crédit sur la montant du
crédit non encore utilisé.
1.8- Modalités de remboursement
Pour l'ensemble des crédits à la construction,
à l'extension et à la surélévation, le
remboursement du prêt intervient un mois après la fin de la
période de différer. Pour ceux concernant l'achat d'un
logement
Quatrième partie Cas pratiques
81
ou d'un terrain, l'aménagement d'une habitation, le
remboursement intervient trente jours après la date de signature du
contrat du prêt.
Selon le choix du client deux (02) modalités de
remboursements sont possibles :
· Remboursement selon la formule de
l'échéance constante ;
· Remboursement selon la formule du principal constant.
1.8.1- Remboursement par échéance
constante
Ce type de remboursement est le plus utilisé par les
emprunteurs, en raison de sa simplicité. Pour comprendre les principes
de cette méthode nous allons prendre un exemple chiffré.
Exemple
Un client vient d'obtenir un crédit immobilier
auprès de la CNEP-BANQUE aux conditions suivantes :
y' Capital : 2 000 000 DA
y' Taux d'intérêt annuel : 6%
y' Durée : 360 mois (30ans)
y' Remboursement mensuel à échéances
constantes.
Pour calculer le montant des mensualités constante nous
allons utiliser la formule suivante :
Montant de la mensualité = K * I
K: capital
I: coefficient, I = im / 1 - (1 +
im)- n
im : taux d'intérêt mensuel n : nombre de
mensualités
|
Donc
|
I = 0.005995
|
|
|
Montant de la mensualité = 11 990 DA
|
o Pour la première mensualité (11 990 DA)
Intérêt = 2 000 000 * 0.005 = 10 000 DA Capital = 11 990 - 10 000
= 1 990 DA
o Pour la deuxième mensualité (11 990)
Intérêt = 1 998 810 * 0.005 = 9 990.05 DA Capital = 11 990 - 9
990.05 = 1 999.95 DA
o Pour la troisième mensualité (11 990)
Intérêt = 1 996 810 * 0.005 = 9 984.05025 DA
Capital = 11 990 - 9 984.05025 = 2 005.94975 DA
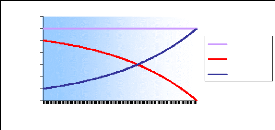
Nous avons étudié l'évolution du
remboursement des intérêts et du capital sur 360 mois et nous
avons obtenu le graphique suivant :
Quatrième partie Cas
pratiques
14000
12000
10000
4000
8000
6000
2000
0
1 45 89 133 177 221 265 309 353
Échéance Intérêt Capital
Graphe représentant l'évolution du
remboursement des intérêts et du capital pour une
échéance constante
Nous constatons que dans cette méthode le remboursement
des intérêts est dégressif, tandis que celui du capital est
progressif.
| 


