CHApiTRE TRois
CROISSANCE DES
NANO-CAVITES/BULLES
La terminologie généralement utilisée dans
la littérature désigne les bulles comme des entités
remplies de gaz tandis que les nano-cavités sont supposées
vides
3.1 CROISSANCE THERMIQUE DES NANO-CAVITES
Après implantation ionique, les
nano-cavités/bulles formées croissent au cours du traitement
thermique (figure 3.1). Pour décrire cette croissance, deux
mécanismes ont été proposés dans la
littérature. Ils peuvent s'appliquer soit aux nano-cavités, soit
aux bulles. Il s'agit des mécanismes d'Oswald Ripening (OR) et de
Migration Coalescence (MC).

FIGURE 3.1: Croissance thermique de nano-cavités, cas
d'implantation de l'As [E. Ntsoenzok].
3.1.1 La Migration Coalescence
Le mécanisme de migration coalescence (MC) suppose que
les nano-cavités/bulles migrent et fusionnent lorsqu'elles se
rencontrent (figure 3.2); c'est un mécanisme de collision
considérant le mouvement des nano-cavités/bulles elles
mêmes. Leurs mouvements sont attribués
au transfert de lacunes dans les nano-cavités.
Le coefficient de diffusion Dc d'une cavité/bulle
dépend à la fois de son rayon (r) et de la pression interne de
l'ion implanté (p). Il prend en compte les mécanismes de
diffusion de la surface et du volume de la bulle/cavité, ainsi que le
transport de l'ion implanté en phase gazeuse. Le coefficient de
diffusion Dc (r, p) étant inversement proportionnel au rayon,
les petites nano-cavités/bulles diffusent plus vite vers les autres
nano-cavités/bulles pour coalescer. Elles ont donc tendance à
disparaitre les premières. D'après ce mécanisme, la
croissance des nano-cavités/bulles s'arrête lorsque leur longueur
de diffusion est supérieure à la distance qui les
sépare.
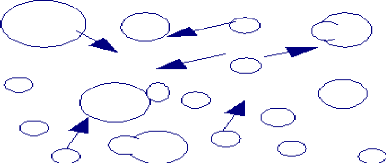
FIGURE 3.2: Processus de migration coalescence.
Ce mécanisme a été modélisé
par J. H. Evans [1] dans le cas d'une étude des mécanismes de
croissance des bulles d'hélium implantées dans le silicium. C'est
un modèle simple dont l'étude révèle des richesses
insoupçonnées. Dans ce modèle, l'équation de base
gouvernant la vitesse de fusion ou de coalescence des
nano-cavités/bulles (ayant un rayon r et une concentration
Cv) migrant aléatoirement a été décrite
et simplifiée pour l'application présente. Elle est de la forme
:
dCv
dt
= 16ðDcrC2 (3.1)
v
De cette équation (voir annexe), il a été
établi une relation entre le rayon des nano-cavités et le temps
de recuit :
~4/3
12S ~4ð
r2 -- r2 o = D5t (3.2)
ð 3
On s'aperçoit qu'effectivement, dans la croissance des
nano-cavités/bulles par la MC, le rayon moyen en fonction du temps de
recuit (t) suit une loi comportementale en /t donnée par
l'équation :
r2--r2 o =Kt (3.3)
Où Dc : coefficient de diffusion d'une
cavité, r : rayon moyen des cavités, S : surface de la
cavité, r0 : rayon moyen initial des cavités, D5 :
coefficient de diffusion surfacique et K une constante.
| 


