3.1.2 L'Oswald Ripening (Maturation d'Oswald)
Ce processus spontané se produit parce que de grandes
particules sont énergétiquement favorisées aux
dépens de petites particules et les petites particules
cinétiquement favorisées aux dépens des grandes. Ceci
s'explique par le rapport volume/surface (que nous noterons Ù S ); les
petites particules ont un Ù S élevé et sont par
conséquent plus facile à produire, contrairement aux grandes
particules qui avec leur Ù S petit, représente un état de
faible énergie (état obtenu en abaissant la température
lors du recuit thermique). De ce fait, les petites particules atteindront un
état de faible énergie si elles sont transformées en
grandes particules; c'est le phénomène de maturation
d'Ostwald.

FIGURE 3.3: Processus d'oswald ripening
Il décrit aussi l'évolution temporelle d'une
structure inhomogène basée sur le fait que les concentrations de
l'atome implanté et de lacunes à la périphérie des
nano-cavités/bulles
sont inversement proportionnelles à leur rayon. Un
gradient de concentration se créé entre les
nano-cavités/bulles de différentes tailles; ce qui conduit la
diffusion de lacunes et d'atomes implantés d'une cavité/bulle
à une autre (figure3.3) à travers la matrice et monopolise la
croissance ou le rétrécissement jusqu'à ce que la taille
des nano-cavités/bulles s'homogénéise ou que les distances
entre les nano-cavités/bulles deviennent trop importantes.
Dans l'approche LSW 1 , le rayon moyen d'une
cavité/bulle suit une loi comportementale en fonction du temps qui
obéît à l'équation :
(4 )
r3 - r3 o = aDct (3.4)
9
Où ro est le rayon moyen initial et a est
proportionnel à l'énergie spécifique d'interface.
En effet, il n'existe pas de difficulté dans
l'application de la maturation d'Oswald (OR) à une population de
nano-cavités/bulles. L'équation maîtresse décrivant
ce mécanisme a été établie par Greenwood et al.[1]
dans une étude approfondie de la croissance des bulles dans les
métaux. Ils trouvèrent à cet effet que le taux de
variation du rayon pouvait s'exprimer comme suit :
dr
dt
(1 ) (2ãI )
= - DcCeq
v exp (3.5)
r rkT
Où Ceq
v : concentration à l'équilibre d'une lacune,
ã : l'énergie surfacique, I : volume de la cavité, k :
constante de boltzman, T : température de recuit.
Sous de bonnes conditions donc, l'OR se produira à
travers la dépendance en 1 r de l'équation, qui doit mener
à la croissance de grosses nano-cavités/bulles aux dépends
des plus petites; le terme en exponentiel dans l'expression du rayon deviendra
donc plus dominant et accélérera rapidement le processus de
rétrécissement. En se rétrécissant, les lacunes de
certaines nano-cavités/bulles seront redistribuées à
d'autres et à la fin on aura un nombre réduit de
nano-cavités/bulles ayant de très grands rayons. Nous pouvons
observer ce phénomène sur la figure 3.4 [8] sur laquelle nous
voyons le nombre de nano-cavités diminuer avec l'évolution
temporelle (pendant le recuit).
Ce mécanisme, du fait de la prise en compte de certains
facteurs, peut très bien limiter la croissance. Par exemple J. Evans a
prédit que l'effet de perte de lacunes à la surface pouvait
limiter la croissance des bulles. C'est pour de telles raisons que certains
chercheurs ont réalisé une étude comparative des deux
mécanismes.
1. La théorie Lifshitz-Slysosov-Wagner
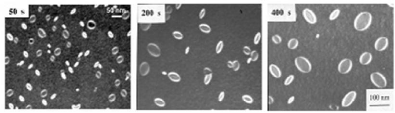
FIGURE 3.4: Croissance de nano-cavités suivant le
mécanisme d'Oswald ripening
| 


