Déterminants des investissements directs étrangers en France.

V.3.1.4 Modélisation du quatrième modèle ARIMA (2, 0, 1) Nous rappelons tout d'abord que l'équation du modèle ARIMA (2, 0, 1) est :

ide_t = u + a_t - 81at_1 + _{çP1idet_1} + çP2idet_2 où :

ide_t représente la série IDE_t

a_t représente le bruit blanc

u représente la tendance centrale de notre série

Nous allons à présent poursuivre avec la vérification des conditions de stationnarité et la significativité des paramètres. Nous essayerons également de vérifier si nos résidus suivent bien un bruit blanc.

66

Tableau 22 : Modélisation ARIMA (2, 0, 1) avec la constante

Evaluations de la fonction : 45
Evaluations du gradient : 16
Modèle 1 : ARMA utilisant les observations 1995 : 1							- 2013 : 4 (T=76)
Paramètres	Coefficient		Erreur Std.		Z		P. critique		Significativité
CONSTANTE	211,699		52,112		4,062		4,86e-05		***
PHI 1	0,534		0,219		2,442		0,015		**
PHI_2	0,294		0,124		2,368		0,018		**
THETA 1	-0,569		0,218		-2,616		0,009		***
							Valeur
Moyenne variable dépendante							229,147
Ecart type variable dépendante							200,893
Moyenne des innovation							3,66324
Ecart type des innovations							184,180
Log de vraisemblance							-504,450
Critère d'Akaike							1 018,901
Critère de Schwarz							1 030,554
Hannan-Quinn							1 023,558
Modèle		Réel		Imaginaire		Modulo		Fréquence
AR
RACINE 1		1,147		0,000		1,147		0,000
RACINE 2		-2,961		0,000		2,961		0,500
MA
RACINE 1		1,756		0,000		1,756		0,000

Dans ce modèle, nous envisageons également des modèle mixtes : ARIMA (2, 0, 1), c'est une combinaison de AR (2) et MA (1). D'après le tableau 22, nous observons que la constante est significative. Par conséquent, elle est conservée dans ce modèle. De plus, PHI_1, PHI_2 et THETA_1 sont également significatifs au seuil de risque de 5% pour PHI et de 1% pour THETA_1. La valeur de PHI_1 est égale à 0,534, PHI_2 est égale à 0,294 et celle de THETA_1 est égale à -0,569. Comme on est dans un modèle mixte, il faut vérifier aussi les conditions de stationnarité et d'inversibilité avant l'estimation. Ici nous avons :

|ö₂| = |0,294| < 1,

P₁ + P₂ = 0,534 + 0,294 = 0,828 < 1,

P₂ - P₁ = 0,294 - 0,534 = -0,240 < 1,

|e₁| = |-0,569| < 1

Donc les conditions de stationnarité et d'inversibilité sont vérifiées.

67

Nous allons à présent examiner les résidus de notre modèle à partir d'un corrélogramme. Nous réaliserons également une représentation de la FAC et de la FACP.

Graphique 25 : Corrélogramme des résidus

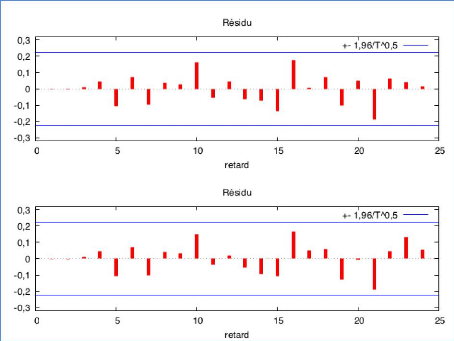
D'après le graphique 25, on peut constater qu'aucun de nos résidus ne dépassent le seuil significatif, donc ils ont une caractéristique d'un bruit blanc.

Tableau 23 : FAC et FACP pour les résidus

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	-0,002	-0,002
2	-0,003	-0,003
3	0,009	0,009
4	0,045	0,045	0,178	0,673
5	-0,108	-0,108	1,149	0,563
6	0,071	0,072	1,571	0,666
7	-0,097	-0,101	2,379	0,666
8	0,036	0,041	2,495	0,777
9	0,026	0,032	2,555	0,862

68

10

	0,161	0,149	4,874	0,675
11	-0,055	-0,038	5,152	0,741
12	0,044	0,021	5,329	0,805
13	-0,063	-0,056	5,707	0,839
14	-0,072	-0,093	6,202	0,860
15	-0,136	-0,105	7,987	0,786
16	0,177	0,165	11,091	0,603
17	0,007	0,052	11,096	0,678
18	0,069	0,060	11,588	0,710
19	-0,104	-0,128	12,706	0,694
20	0,051	-0,007	12,977	0,738
21	-0,190 *	-0,188	16,851	0,533
22	0,061	0,046	17,264	0,572
23	0,039	0,130	17,437	0,624
24	0,015	0,054	17,464	0,683

D'après le tableau 23, on constate que la p-value est égale à 0,683 ce qui est supérieure à 0,05. Les résidus sont donc indépendants entre eux. La p-value étant relativement élevée, on peut donc dire que le modèle est bon.

Graphique 26 : Test de normalité des résidus

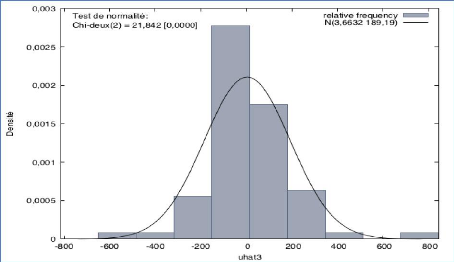
D'après le graphique 26, on a une p-value égale à 0,0000, ce qui est inférieure à 0,05, donc on rejette H0 et nos résidus ne suivent pas une loi normale.

69

Graphique 27 : Les valeurs observées et prédites

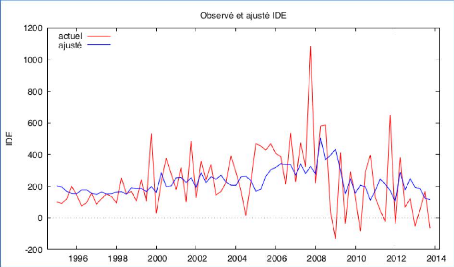
D'après le graphique 27, on observe visuellement que les deux lignes ont des tendances et des volatilités différentes. Nos qualités prédites semblent décevantes.