Déterminants des investissements directs étrangers en France.

V.3.1.2 Modélisation du second modèle MA (2) Pour commencer, rappelons que l'équation du modèle MA (2) est :

???????? = ?? + ???? - ??1????-1 - ??2????-2 où :

???????? représente la série ????????

???? Représente le bruit blanc

?? Représente la tendance centrale de notre série

Nous allons à présent contrôler à partir du modèle réalisé sous le logiciel GRETL la significativité des paramètres.

Tableau 19 : Modélisation MA (2) avec la constante

Evaluations de la fonction : 38
Evaluations du gradient : 13
Modèle 1 : ARMA utilisant les observations 1995 : 1											- 2013 : 4 (T=76)
Paramètres		Coefficient			Erreur Std.			Z			P. critique			Significativité
CONSTANTE		227,566			26,912			8,456			2,77e-17			***
THETA_1		-0,030			0,119			-0,254			0,800
THETA 2		0,263			0,104			2,524			0,012			**
											Valeur
Moyenne variable dépendante											229,147
Ecart type variable dépendante											200,893
Moyenne des innovation											0,730
Ecart type des innovations											191,279
Log de vraisemblance											-507,195
Critère d'Akaike											1 022,390
Critère de Schwarz											1 031,713
Hannan-Quinn											1 026,116
Modèle	Réel			Imaginaire			Modulo			Fréquence
MA
RACINE 1	0,058			-1,949			1,950			-0,245

61

RACINE 2

0,058

1,949

1,950

0,245

Ensuite, nous avons modélisé le modèle MA (2). D'après le tableau 19, nous observons que la probabilité de la constante est inférieure à 0,05. Par conséquent, elle est significative donc nous la conservons dans le modèle. De plus, THETA_2 est significatif au seuil de risque de 5%. La valeur de THETA_2 est égale à 0,263. En revanche, THETA_1 n'est pas significatif donc nous allons observer notre troisième modèle. Les graphiques de ce modèle MA (2) se trouvent en fin de dossier (annexe 5).

V.3.1.3 Modélisation du troisième modèle ARIMA (1, 0, 1) Nous rappelons tout d'abord que l'équation du modèle ARIMA (1, 0, 1) est :

ide_t = u + a_t - 81at_1 + (P1idet_1 où :
ide_t représente la série IDE_t
a_t représente le bruit blanc
u représente la tendance centrale de notre série

Nous allons à présent s'assurer à partir du modèle obtenu sous le logiciel GRETL que les conditions de stationnarités sont vérifiées ainsi que la significativité des paramètres. Nous essayerons également d'observer si nos résidus suivent bien un bruit blanc.

Tableau 20 : Modélisation ARIMA (1, 0, 1) avec la constante

Evaluations de la fonction : 59
Evaluations du gradient : 19
Modèle 1 : ARMA utilisant les observations 1995 : 1							- 2013 : 4 (T=76)
Paramètres	Coefficient		Erreur Std.		Z		P. critique		Significativité
CONSTANTE	207,645		56,736		3,660		0,000		***
PHI 1	0,920		0,076		12,100		1,12e-33		***
THETA 1	-0,786		0,104		-7,588		3,26e-14		***
							Valeur
Moyenne variable dépendante							229,147
Ecart type variable dépendante							200,893
Moyenne des innovation							4,385
Ecart type des innovations							190,174
Log de vraisemblance							-506,815
Critère d'Akaike							1 021,630
Critère de Schwarz							1 030,953
Hannan-Quinn							1 025,356

62

Modèle

	Réel	Imaginaire	Modulo	Fréquence
AR
RACINE 1	1,087	0,000	1,087	0,000
MA
RACINE 1	1,272	0,000	1,272	0,000

Dans ce modèle, nous envisageons des modèle mixtes : ARIMA (1, 0, 1), c'est une combinaison de AR (1) et MA (1). Cela veut dire que la performance présente est déterminée par la performance précédente et la valeur de référence évolue d'une mesure à l'autre. L'objectif essentiel de la modélisation est de déterminer combien de paramètre est nécessaires pour obtenir un modèle effectif. D'après le tableau 20, nous observons que la constante est significative. Par conséquent, elle est conservée dans ce modèle. De plus, PHI_1 et THETA_1 sont également significatifs au seuil de risque de 1%. La valeur de PHI_1 est égale à 0,920 et celle de THETA_1 est égale à -0,786. Comme on est dans un modèle mixte, il faut vérifier aussi les conditions de stationnarité et d'inversibilité avant l'estimation. Ici nous avons :

|ö₁| = |0,920| < 1,

|e₁| = |-0,786| < 1

Donc les conditions de stationnarité et d'inversibilité sont vérifiées.

Nous allons à présent vérifier les résidus de notre modèle à partir d'un corrélogramme. Nous ferons également une représentation de la FAC et de la FACP.

Graphique 22 : Corrélogramme pour les résidus

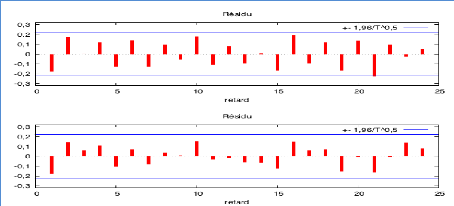
63

Dans cette étape de l'estimation, les vérifications essentielles à réaliser portent sur les résidus. Les valeurs de la fonction d'autocorrélation et d'autocorrélation partielle de la série des résidus doivent être toutes égales à zéro. Cela veut dire qu'ils ont une caractéristique qui correspond à celle d'un bruit blanc. Si les autocorrélations et les autocorrélations partielles ne sont pas nulles, on pourrait dire que le modèle ARIMA est probablement inapproprié. Ici on peut constater qu'aucun de nos résidus ne dépassent le seuil significatif, donc ils ont une caractéristique d'un bruit blanc.

Tableau 21 : FAC et FACP pour les résidus

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	-0,180	-0,180
2	0,173	0,145
3	0,000	0,056	4,952	0,026
4	0,121	0,111	6,157	0,046
5	-0,127	-0,106	7,497	0,058
6	0,139	0,072	9,136	0,058
7	-0,129	-0,078	10,578	0,060
8	0,093	0,035	11,327	0,079
9	-0,052	0,006	11,568	0,116
10	0,181	0,152	14,521	0,069
11	-0,111	-0,033	15,648	0,075
12	0,082	-0,019	16,268	0,092
13	-0,092	-0,063	17,067	0,106
14	0,007	-0,066	17,072	0,147
15	-0,166	-0,123	19,745	0,102
16	0,194 *	0,148	23,461	0,053
17	-0,092	0,060	24,304	0,060
18	0,120	0,071	25,766	0,057
19	-0,166	-0,154	28,637	0,038
20	0,134	-0,005	30,552	0,032
21	-0,228 **	-0,164	36,148	0,010
22	0,093	-0,006	37,108	0,011
23	-0,030	0,138	37,206	0,016
24	0,048	0,079	37,468	0,021

Dans cette approche de Box et Jenkins, un autre test statistique souvent employé pour évaluer un bruit blanc est le test Q. Ce test dont le but est de vérifier si les résidus sont indépendants entre eux. Nous devons vérifier l'hypothèse H0 d'indépendance entre les résidus. Si la p-value est supérieure à 0,05, on accepte l'hypothèse H0 et on dira que les résidus sont indépendants. Dans le cas où la p-value est inférieure à 0,05, on refuse

64

l'hypothèse H0 et par conséquent, les résidus ne seront pas indépendants. D'après le tableau 21, on constate que la p-value est inférieure à 0,05. Les résidus ne sont donc pas indépendants entre eux.

Graphique 23 : Test de normalité des résidus

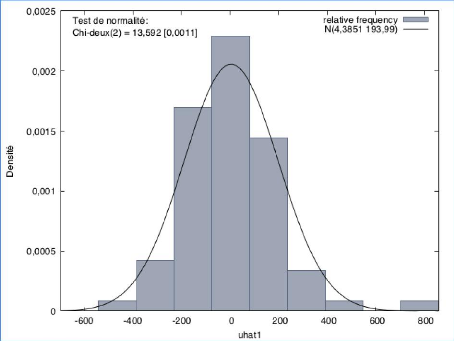
D'après le graphique 23, on peut voir si les résidus suivent une loi normale. On pose l'hypothèse H0 : les résidus suivent une loi normale. Il faut une p-value supérieure à 0,05 pour accepter H0, ici on a une p-value égale à 0,0011, ce qui est inférieure à 0,05, donc on rejette H0 et nos résidus ne suivent pas une loi normale.

65

Graphique 24 : Les valeurs observées et prédites

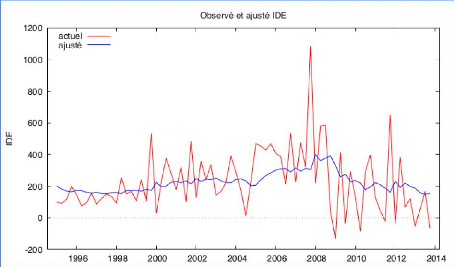
Tout d'abord, si le modèle est bien spécifié, l'ajustement réalisé selon ce modèle doit suivre les évolutions de la série empirique, donc on projette les valeurs observées et les valeurs prédites dans le même graphique. Selon le graphique 24, on constate visuellement que les deux lignes ont des tendances et des volatilités différentes. Nos qualités prédites ne sont pas satisfaisantes.