3.4 Propriétés électroniques :
3.4.1 Structure des bandes et densité
d'état électronique :
En physique de la matière condensée, la
densité d'état électronique DOS quantifie le nombre
d'états électroniques susceptibles d'être occupés,
et possédant une énergie donnée dans le matériau
considéré. Dans cette partie, nous nous sommes
intéressés aux calculs des structures de bande d'énergie
et les densités d'états électroniques du dioxyde de titane
anatase, en utilisant les paramètres optimisés du réseau.
Les niveaux d'énergie des électrons sont décrits en termes
de fonctions continues En, k (ou En(k)) qui ont la périodicité du
réseau réciproque. Ces fonctions En(k) définissent la
structure de bande.
L'entier n est appelé indice de bande, et k est une
variable continue de l'espace des k, limitée
à la première ZB. Elle s'écrit dans le
cas d'un système de dimension trois :
Equation 3.2 ??(E) = ? ? ??????
???????? ???????? (E -
E????)
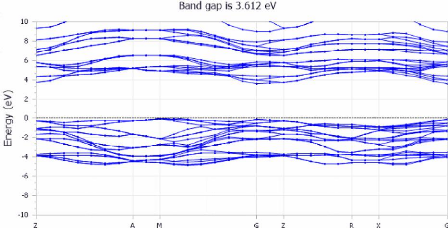
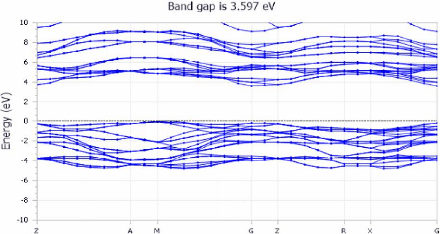
Les figures (3.9) et (3.10) montre respectivement les structures
des bandes et les densités électroniques DOS obtenues par DFT.

Chapitre III Résultats et
discussions
45 | P a g e
DFT/LDA

DFT/GGA-PBE
Chapitre III Résultats et
discussions
46 | P a g e
DFT/GGA-PBEsol
DFT/GGA+U
FIGURE 3.9 - Les structures des
bandes du TiO2 anatase

Chapitre III Résultats et
discussions
DFT/LDA

DFT/GGA-PBE
DFT/GGA+U
47 | Page
Chapitre III Résultats et
discussions
48 | P a g e
DFT/GGA-PBESOL
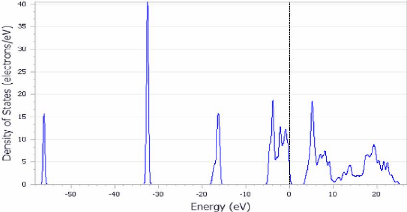
FIGURE 3.10 - Les densités
d'état électronique DOS du TiO2 anatase
Dans le cadre du présent travail, les structures de
bandes électroniques ont été déterminées par
un calcul DFT dans les approximations du gradient
généralisé LDA, GGA-PBE, GGA+U, et GGA- PBEsol.
Pour chaque méthode utilisée nous avons fait
l'optimisation de la géométrie avec le code CASTEP puis on a
effectué le calcul. D'une autre part, c'est très important ; pour
chaque calcul nous avons fait l'optimisation et le calcul des
propriétés avec la mémé approximation.
Les structures des bandes sont représentées dans
l'espace réciproque pour simplifier les calculs. Les calculs ont
été réalisés le long des différents points
et directions de haute symétrie dans la première zone de
Brillouin dans le but de déterminer la valeur de gap
énergétique de ce matériau. Les calculs ont
été effectués en utilisant plusieurs approximations
Les points de haute symétrie : Z--G G--X X--P P--N
N--G.
Le niveau de Fermi Ef est toujours pris comme une origine
d'énergies Ef = 0.
Une possibilité pour contourner les limitations serait
avec GGA+U et d'augmenter le potentiel GGA par la correction d'Hubbard pour
décrire les fortes interactions coulombiennes intra-site
écrantées entre les électrons d.
Cette correction est effectuée avec Ud = 8.5,
nous avons trouvé Eg = 3.597 eV.
Chapitre III Résultats et
discussions
49 | P a g e
A première vue, Les figures (3.9) montrent que : le
composé étudié, est un semi-conducteur à bande
interdite directe (gap direct) puisque le maximum de la bande de valence BV et
le minimum de la bande de conduction BC sont en coïncidence, ils se
trouvent sur la même ligne passant par le point de haute symétrie.
Cette résultat est bien en accord avec l'expérimentale. La bande
de conduction est située au-delà de 3.301 eV et la bande de
valence au-dessous de niveau de Fermi.
Les figures (3.10) montrent aussi que la valeur du DOS de la
phase anatase est importante autour de niveau de Fermi, ce qui prouve la nature
métallique de cette phase.
Méthode LDA GGA-PBE GGA+U GGA-PBESOL EXP Autre
calcul
Bande 3.53 3.607 3.597 3.612 3.6
Mbj 3.01
interdite GW 3.56
TABLEAU 3.4 - Les valeurs de
l'énergie de gap obtenue [40]
D'après les résultats du (tableau 3.3), l'on
arrive à constater que le gap calculé est proche de valeur
théorique de GW et proche aussi de valeur expérimentale.
| 


