Conclusion :
Dans ce chapitre nous avons présenté tous les
méthodes de simulation et les matériels utilisés. En
premier, nous avons présenté la technique « Spray Pyrolyse
» pour l'élaboration des couches minces de dioxyde de titane TiO2.
Par la suite, nous avons explicité le logiciel de simulation «
Materials Studio » ainsi le code serveur « CASTEP ».
D'une autre part, nous avons terminé ce chapitre par la
méthode de simulation « Dynamique Moléculaire Simulation
».
36 | Page
Chapitre III
Résultats et discussions
Chapitre III Résultats et
discussions
37 | Page
3.1 Le détail de calcul :
Dans notre travail, nous avons effectué le calcul des
premiers principes au sein de la faculté des sciences de Gafsa. Ce
calcul ab-initio est basé sur la théorie de la fonctionnelle de
la densité DFT. En utilisant la méthode d'ondes planes et
pseudo-potentielles implémentées dans le code CASTEP de Materials
Studio.
La première étape consiste à optimiser le
nombre de points spéciaux « k » pour le maillage de la
première zone de Brillouin partir d'une mèche fine.
Les énergies d'interactions d'échanges et de
corrélations sont évaluées par les approximations de LDA,
GGA-PBE, PBEsol, GGA + U et la fonctionnelle B3LYP.
Tous les travaux sont effectués avec le dioxyde de
titane anatase. Cette phase est de symétrie tétragonal, et
décrit par le groupe d'espace I41/amd. Les paramétres
de maille sont
respectivement les suivants : a = b = 3.780 A, c = 9.510 A et
C/?? = 2.51 > 1.
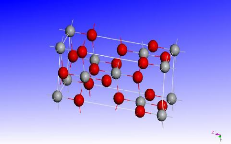
FIGURE 3.1 - Structure
cristalline du dioxyde de titane anatase
3.2 Optimisation de la géométrie :
La tâche d'optimisation de la géométrie
est le point de départ de tous les calculs, quel que soit le calcul et
quel que soit le code utilisé. Comme on a dit dans le chapitre
précèdent, elle est très importante pour que la structure
soit parfaitement stable pour qu'on puisse calculer les
propriétés recherchés.
Nous avons utilisé le code CASTEP dans Materials Studio
pour faire l'optimisation de TiO2 anatase et on répète
l'optimisation jusqu'on obtient la convergence.
Chapitre III Résultats et
discussions
38 | P a g e
Dans le but de connaitre la valeur de l'énergie de
coupure nécessaire pour notre calcul nous avons fait un petit
diagnostic. Nous avons fait plusieurs calculs par plusieurs valeurs (100, 200,
300, 450, 500, 550, 600 eV) d'énergie de coupure pour une bonne
convergence.
Le tableau suivant montre les différentes valeurs de
convergence :
|
Energie de
|
|
|
|
|
|
|
|
|
coupure en (eV)
|
100
|
200
|
300
|
450
|
500
|
550
|
600
|
|
Energie de convergence en (eV)
|
-384.194
|
-423.261
|
-429.213
|
-429.579
|
-429.598
|
-429.599
|
-429.634
|
TABLEAU 3.1 - Variation de la
convergence en fonction des différentes valeurs d'énergie
de coupure

FIGURE 3.2 - Variation de la
convergence en fonction de l'énergie de coupure
Chapitre III Résultats et
discussions
39 | P a g e
La figure (3.2) montre que la convergence à partir de -
429 eV reste la même valeur pour les énergies de coupures 450,
500, 550 et 600 eV. On comprend alors que la valeur adéquate de
l'énergie de coupure est 450 eV.
Dans ce cadre, l'optimisation de la géométrie
est réalisée sur une base d'ondes planes avec une énergie
de coupure de de 450 eV. Nous avons utilisé les potentiels Ultrasoft et
le potentiel a norme conservé pour décrire l'interaction entre
les électrons de coeur et les ions du coeur.
La méthode de Monkhorst - Pack avec des k - points
(3×3×2) est aussi utilisé pour simplifier la zone de
Brillouin. Pour décrire la fonctionnelle
d'échange-corrélation Exc., nous avons utilisé la
fonctionnelle GGA-BPE.
Nous avons obtenu la convergence après 7
itérations, avec une énergie 2.98.10-5 ev/atom, et un
maximum de force ionique 5.93.10-3 eV/Å. Le maximum de
déplacement entre les cycles d'itérations est
8.030.10-4 Å et le maximum de pression 8.669.10-2
GPa. Les figures (3.3) ci-dessous montrent les différentes étapes
d'optimisation, la convergence et l'optimisation en fonction de
l'énergie.

(A)

(B) (C)
FIGURE 3.3 - (A) Structure avant
l'optimisation, (B) et (C) : Optimisation de la géométrie
du TiO2

Chapitre III Résultats et
discussions
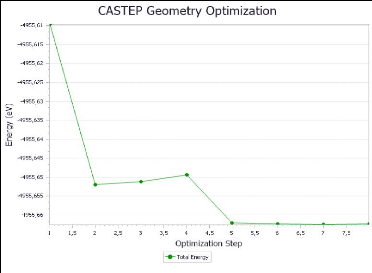
FIGURE 3.4 - La convergence
d'optimisation avec CASTEP
40 | P a g e
FIGURE 3.5 - L'optimisation de la
géométrie du TiO2 anatase en fonction d'énergie
Chapitre III Résultats et
discussions
41 | P a g e
3.3 Spectre Raman :
La spectroscopie Raman est une méthode de
caractérisation des vibrations de réseaux cristallins. On cherche
toujours à observer les modes de vibration du réseau cristallin
par l'identification des différentes modes de vibrations. Le calcul est
basé sur la théorie de la DFT. Pour décrire l'interaction
d'échange - corrélation, nous avons utilisé la
fonctionnelle hybride B3LYP.
|
a
|
b
|
C
|
Alpha
|
Beta
|
Gamma
|
|
3.7617561 Å
|
3.7617561 Å
|
3.7617561 Å
|
90.00000
|
90.00000
|
90.00000
|
(a)
|
x
|
Y
|
Z
|
O ( 8 )
|
4.656804416270E-17
|
2.500000000000E-01
|
1.721700410720E-01
|
Ti ( 22 )
|
5.000000000000E-01
|
-2.500000000000E-01
|
-1.250000000000E-01
|
|
(b)
TABLEAU 3.2 - (a)
Paramétres de maille de l'anatase, (b) Coordonnées
cartésiens
Les figures (3.6) et (3.7) montre respectivement les spectres
Raman du TiO2 anatase expérimentale et théorique obtenue par
DFT/B3LYP.

Figure 3.6 - Spectres Raman
expérimentale du TiO2 anatase

Chapitre III Résultats et
discussions
42 | P a g e
Figure 3.7 - Spectres Raman du
TiO2 anatase DFT/B3LYP
La maille de l'anatase est tétragonal appartient au groupe
d'espace D4h
19 (I41 ?? ????). La maille
primitive de l'anatase possède deux groupements TiO2 (donc
6 atomes) par maille ce qui conduit a 15 modes de vibrations possibles (3 x 6 -
3).
La théorie des groupes donne la représentation
irréductible suivante pour les vibrations optiques de l'anatase [35]:
Equation 3.1 ???????? + ?????? ?? + ???????? + ????????
+ ?????? + ??????
Les modes ??????, ?????? et ???? sont actifs en spectroscopie
Raman et les modes ?????? et ???? sont actifs en spectroscopie infrarouge. Par
contre, le mode ?????? est inactif ni en spectroscopie Raman ni en
spectroscopie infrarouge.
Chapitre III Résultats et
discussions
43 | P a g e
En spectroscopie Raman il y a 6 modes de vibrations permis.
Les modes actifs en spectroscopie Raman sont les quatre modes ??????,??????,
?????? et ????, les autres sont actifs en spectroscopie infrarouge et le mode
A2g est silencieux [36].
La figure (3.6) [37] montre 4 pics c'est à dire 6
bandes situées respectivement à 144 cm bande ????, à 398
cm bande ?????? , à 515 cm bande ?????? et a 639 cm bande ????.. Nous
constatons que le premier pic est la raie la plus intense ????. Cette pic
désigne toujours la raie référence parce qu'elle est la
plus intense et la plus fine ce qui facilite l'observation de ses
déplacements.
La troisième raie est un doublé de deux raies 513
?????? et 519 ??????.
On remarque que les pics de spectre Raman obtenue par
DFT/B3LYP (figure (3.7)) sont les mêmes pics obtenus
expérimentalement (figure 3.6)).
Alors on déduit que notre calcul DFT avec la
fonctionnelle hybride B3LYP est en bon accord avec l'expérimentale.
Dans le tableau (3.3) ci-dessous, nous présentons les
modes de vibrations et la fréquence en (nm) associé à
chaque mode.
|
Mode
|
Fréquence (nm)
|
|
Eg
|
144
|
|
B1g
|
398
|
|
A1g
|
514
|
|
B1g
|
519
|
|
Eg
|
639
|
TABLEAU 3.3 - Fréquences des
différentes bandes Raman de la phase anatase du TiO2 [38]
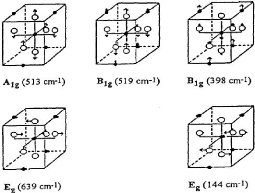
Pour chaque mode de vibration, nous présentons
ci-dessous la figure (3.8) les modes de vibrations et de déplacements
des atomes [39].
Chapitre III Résultats et
discussions
44 | P a g e
Figure 3.8 - Schéma des
déplacements des atomes pour les différentes modes des
vibrations
| 


