IV.4.2. Temps de parcours régularisé et
traçage des horaires pour une course
L'étude n'a jusque-là permis l'analyse de la
situation qu'en partant du Campus. Il y a lieu à croire que les usagers
attendant le bus depuis l'autre bout n'embarqueront qu'après
l'arrivée et le débarquement du Bus1 quittant le Campus. Les
horaires prévus pour le cas des bus de la flotte parcourant la ligne du
Campus vers la Gare sont textuellement repris pour illustrer le parcours
Gare-Campus.
Les hypothèses soutenues pour accommoder le temps
théorique de parcours au temps réel sont les suivantes :
· le bus s'arrête pendant 0,5 minutes ou 30 secondes
à chacun des 13 points d'arrêt bus ;
· la vitesse commerciale est de 30 km/h ;
· les bouchons sont peu présents et les
perturbations ne trainent que quelques minutes.
Le temps fixé de parcours est de 20 minutes aller sans
battement, le temps d'arrêt en pleine ligne et le temps de perturbation
due à la congestion s'évaluent comme suit :
Temps de parcours = temps theorique + temps
d'arret + temps des impreyus
Le temps théorique se calcul par la formule de MRU :
x = y * t -+ t = vv sachant que l'espace vaut 6 km et la vitesse 30
km/h :
46
Le temps qu'on devra allouer aux perturbations ou temps des
imprévus sera la différence entre les 20 minutes fixées de
temps de parcours et la somme des temps théorique et d'arrêt.
T???????? ?????? ???????????????? = temps de parcours - ?
temps(théorique; arret)
? T???????? ?????? ???????????????? = 20 minutes - (12 + 6,5)
= 1,5 minutes ou 90 secondes comme temps des imprévus.
Dans la réalité des choses, il n'est presque
pas possible que le bus s'arrête à chaque point d'arrêt. De
ce fait, on suppose qu'il ne s'arrête que cinq fois, ce qui donne 2,5
minutes de temps d'arrêt pour générer 5,5 minutes de temps
pour imprévus ou perturbations. La vitesse commerciale devra être
changer qu'en cas de force majeur, où la conformité au tableau de
marche l'exige pour rester proche de la prévision optimale de parcours.
Le parcours de la ligne dans les deux directions : Campus-Gare et Gare-Campus,
est illustré par la figure 15 ci-dessous.
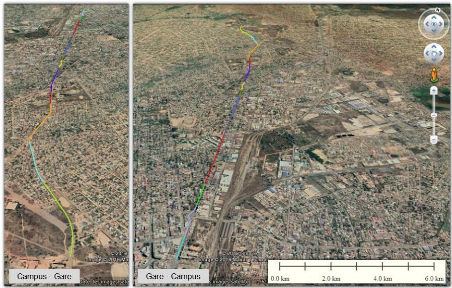
Figure 15 : parcours aller et retour sur la ligne
Campus-Gare
La différence de couleurs sur la figure ci-dessus
représente les tronçons entre arrêt amont et arrêt
aval. La numérotation associée aux noms des arrêts plus
leur positionnement se trouve classer dans les annexes. La qualité de
service à rendre aux usagers dépend de la construction du tableau
de marche, regorgeant l'optimisation de l'offre de service en fonction des
objectifs et en respectant les contraintes d'exploitation. Les horaires et la
régularité de passage de bus aux arrêts pour la flotte
requise, se représentent par une opération qu'on appelle
graphitage. Le graphitage exige à ce qu'on représente chaque
point d'arrêt de bus avec l'heure de passage du bus, exigence qu'on peut
respecter par analyser du trajet.
47
Les horaires de passage de bus à chaque arrêt de
la ligne sont tracés en se référant au tableau de marche,
à la phase de conception. Celle-ci a permis de dresser le tableau 8
(coordonnées espace-temps Campus-Gare). On souhaite sortir de la phase
conceptuelle en simulant la marche réelle, c'est la phase réelle
qu'illustre le tableau 9. Pour y arriver, l'analyse de la mobilité a
permis la modélisation via des relations mathématiques pouvant
faciliter le calcul du temps d'arrivée et de départ d'un bus par
arrêt de la ligne. La procédure de calcul est la suivante :
· chercher le temps théorique/arrêt : tth =
??` dont xi : distance depuis l'origine et v ; ??
vitesse commerciale régularisée = 30 km/h ;
· trouver le produit (perturbation et imprévu) :
37»(n-1) : arrivée et 37»(n) : départ ;
· connaitre au préalable le temps de sortie du bus
de l'arrêt d'origine : tsort ;
· écrire les formules du T d'arrivée et de
départ du bus d'un quelconque arrêt de la ligne :
? Tarr = tsort + 37?(n - 1) + tth C'est le
temps d'arrivée du bus.
? Tdep = tsort + 37?(n) + tth C'est le
temps de départ du bus ;
· le n représente le numéro de l'arrêt
depuis l'origine et sera pris de 2 à 14 dans ce cas.
Tableau 9 : confection des horaires / arrêt course 6 :30'
à 6 :50' dans les deux directions
|
Campus-Gare
|
|
|
|
Nom de
l'arrêt bus
|
Gare-Campus
|
|
|
|
Arrêt
(n)
|
Distance
depuis 1
(km)
Xi
|
|
Temps
|
|
|
Arrêt
(n)
|
Distance
depuis 1
(km)
Xi
|
Temps
|
|
|
|
Arrivée
|
|
Départ
|
Départ
|
|
Arrivée
|
|
1
|
0
|
|
`'
|
|
|
|
|
Campus
|
14
|
5,87
|
6
|
:50'
|
:22»
|
|
|
|
|
|
|
6
|
:30'
|
:00»
|
|
|
|
6
|
:49'
|
:45»
|
|
2
|
0,68
|
6
|
:31'
|
:58»
|
|
|
|
Docteur
|
13
|
5,19
|
6
|
:48'
|
:23»
|
|
|
|
|
|
|
6
|
:32'
|
:35»
|
|
|
|
6
|
:47'
|
:46»
|
|
3
|
1,22
|
6
|
:33'
|
:40»
|
|
|
|
Dispensaire
|
12
|
4,65
|
6
|
:46'
|
:42»
|
|
|
|
|
|
|
6
|
:34'
|
:17»
|
|
|
|
6
|
:46'
|
:05»
|
|
4
|
1,91
|
6
|
:35'
|
:40»
|
|
|
|
Géologie
|
11
|
3,96
|
6
|
:44'
|
:42»
|
|
|
|
|
|
|
6
|
:36'
|
:17»
|
|
|
|
6
|
:44'
|
:05»
|
|
5
|
2,2
|
6
|
:36'
|
:52»
|
|
|
|
Don bosco
|
10
|
3,67
|
6
|
:43'
|
:30»
|
|
|
|
|
|
|
6
|
:37'
|
:29»
|
|
|
|
6
|
:42'
|
:53»
|
|
6
|
2,86
|
6
|
:38'
|
:48»
|
|
|
|
Carrefour
|
9
|
3,01
|
6
|
:41'
|
:34»
|
|
|
|
|
|
|
6
|
:39'
|
:25»
|
|
|
|
6
|
:40'
|
:57»
|
|
7
|
3,1
|
6
|
:39'
|
:54»
|
|
|
|
Carocèle
|
8
|
2,77
|
6
|
:40'
|
:28»
|
|
|
|
|
|
|
6
|
:40'
|
:31»
|
|
|
|
6
|
:39'
|
:51»
|
|
8
|
3,31
|
6
|
:40'
|
:56»
|
|
|
|
Kibathi
|
7
|
2,56
|
6
|
:39'
|
:26»
|
|
|
|
|
|
|
6
|
:41'
|
:33»
|
|
|
|
6
|
:38'
|
:52»
|
|
9
|
3,81
|
6
|
:42'
|
:33»
|
|
|
|
Mahenge
|
6
|
2,06
|
6
|
:37'
|
:49»
|
|
|
|
|
|
|
6
|
:43'
|
:10»
|
|
|
|
6
|
:37'
|
:12»
|
|
10
|
4,29
|
6
|
:44'
|
:07»
|
|
|
|
Kiwele
|
5
|
1,58
|
6
|
:36'
|
:14»
|
|
|
|
|
|
|
6
|
:44'
|
:44»
|
|
|
|
6
|
:35'
|
:37»
|
|
11
|
5,06
|
6
|
:46'
|
:17»
|
|
|
|
Ndjamena
|
4
|
0,81
|
6
|
:34'
|
:05»
|
|
|
|
|
|
|
6
|
:46'
|
:54»
|
|
|
|
6
|
:33'
|
:28»
|
|
12
|
5,33
|
6
|
:47'
|
:26»
|
|
|
|
Aéroport
|
3
|
0,54
|
6
|
:32'
|
:55»
|
|
|
|
|
|
|
6
|
:48'
|
:03»
|
|
|
|
6
|
:32'
|
:18»
|
|
13
|
5,66
|
6
|
:48'
|
:43»
|
|
|
|
Kassapa
|
2
|
0,21
|
6
|
:31'
|
:39»
|
|
|
|
|
|
|
6
|
:49'
|
:20»
|
|
|
|
6
|
:31'
|
:02»
|
|
14
|
5,87
|
6
|
:49'
|
:45»
|
|
|
|
Gare
|
1
|
0
|
6
|
:30'
|
:00»
|
|
|
|
|
|
|
6
|
:50'
|
:22»
|
|
|
|
|
`'
|
|
|
48
La régularité est le critère le plus
important pour les utilisateurs de transport collectif. Une fois
déterminé le design de la ligne, les bus doivent respecter les
fréquences annoncées. Malheureusement, les bus sont
confrontés à de nombreux éléments perturbateurs.
Aussi leur temps de parcours n'est-il pas toujours celui prévu par
l'autorité organisatrice des transports. Un phénomène
observé en de nombreuses occasions est l'apparition de trains de bus,
des groupes de véhicules appartenant à la même ligne et
arrivant ensemble à un arrêt. Ce phénomène est en
partie responsable de l'image négative associée aux transport
collectif. (Hans, 2017) La figure 16 illustre comment la perturbation provoque
le retard et le non-respect de temps prévu de parcours d'un bus, en
créant les trains de bus.
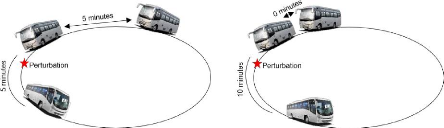
Figure 16 : apparition de trains de bus sur la ligne
La réalisation des horaires, la construction du tableau
de marche et l'application des actions de régulation ne sont possible et
faisable que si l'ensemble du réseau de transport est géré
par une société. Il sera utopique de vouloir organiser la
circulation d'un système mixte, en partie géré par les
particuliers, et par une société.
| 


