III.3.2. Profils en travers (PT)
Les profils en travers sont des sections transversales
perpendiculaires à l'axe du projet, qui permettent de calculer les
paramètres suivants :
? la position des points théoriques d'entrée en
terre des terrassements ; ? l'assiette du projet et son emprise sur le terrain
naturel ;
? les cubatures (volumes de déblais et de remblais).
Le terrain a un fort penchant vers la droite (observateur en
A) et naturellement, les eaux s'écoulent dans la direction A'A (figure
profil en long). Cet'analyse conduit au choix du profile en devers (p = 2 %)
qu'en chevron, pour minimiser les dépenses de construire deux
fossés latéraux.
Toute la zone prévue pour l'emplacement du nouvel
arrêt devra être décapée, il n'est d'office, d'aucune
utilité de faire l'avant métré de terrassement partant du
traçage des profils en long. Néanmoins, les PT d'A et d'A' sont
respectivement représentés sur la figure suivante.
La chaussée mesure 16 m dont, 10 m prévus pour
la circulation et 6 pour le stationnement d'automobile (3 m par
coté).
Les eaux seront évacuées par le seul
fossé de droite qui aura pour dimensions : hauteur 0,8 m et 0,6 m de
largeur. Il y aura lieu à vérifier les dimensions du fossé
pour avoir une capacité d'évacuation (débit
installé) supérieure au débit d'eau de pluie ruisselant la
zone.
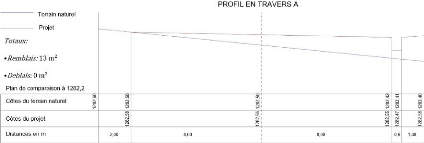

Figure 8 : profil en travers
31
III.3.3. Calcul de la clothoïde
1
La clothoïde (spirale) est la courbe dont la courbure ?? =
est proportionnelle au
??
développement à partir de l'origine. Le recours
à cette courbe se justifie par le souci d'avoir un changement progressif
du rayon par opposition au changement brusque que pouvait procurer la courbe
circulaire simple. Elle a pour équation intrinsèque :
??= ??2 * ??? ??* ??= ??2

Figure 9 : courbe de raccordement en plan
Les données à intégrer dans le calcul du
raccordement de la clothoïde sont : n = 2 voies à sens unique,
R(rayon) = 700 m, â (angle de deux alignements) = 182 gones >
át = 200 - 182 = 18 gones, ?? = 180 ??.
Le Calcul de la clothoïde et la vérification du
type de raccordement à considérer s'effectue comme suit :
|
?
|
??
??
|
=
|
??
??
|
180
=
700
|
= 0,257 Cette valeur se situe entre les lignes 500 et 510 des
abaques en annexeI.
|
?? ?? ??
= = 0,2601 ? ?? = ?? *
?? ?? ??
= 700 * 0,2601 = 182,07 ??.
Partant de la condition L = 180 m, il y a lieu à
considérer le rapport ?? = 0,2601 de la ligne 510.
??
32
Par lecture des valeurs de la ligne 510, T = 8,2792 ??????????
:
? a = at - 2T = 18 - 2(8,2792) = 1,4416 < 10
??????????. Ce calcul vérifie le choix du raccordement clothoïde
suivie d'une autre clothoïde en supprimant la courbe circulaire entre
elles.
L'angle T = ?2 ??? = 2 18= 9, ce qui conduit à
la représentation de la situation d'approche ci-dessous :
8,9413 9 9,2819
530 540 - 10(k) 540
Par interpolation : k = (9,2819-9)
(9,2819-8,9413) = 0,0587
0,3406 = 0,828 * 10 = 8,28 ? 540 - 8,28 = 531,72
8,9413 9 9,2819
530 531,72 540
Les valeurs de la clothoïde unitaire ainsi que celles de la
clothoïde réelle sont calculées dans le tableau
ci-dessous.
Tableau 3 : calcul de la clothoïde par interpolation
|
|
Clothoïde
unitaire
(1) + (3)
(4)
|
Clothoïde réelle
(4) * ??(376,8)
|
|
Ligne 530
(1)
|
?= 540 - 530
(2)
|
(2) * k(0,828)
(3)
|
|
0,003285
|
255
|
211
|
0,003496
|
0,003496
|
|
|
??
r
|
0,2809
|
10700
|
8860
|
1,1669
|
1,1669
|
|
|
8,9413
|
3406
|
2820
|
9
|
9
|
|
|
0,5300
|
1000
|
828
|
0,6128
|
231
|
|
|
0,52896
|
989
|
819
|
0,53715
|
202,4
|
|
|
0,02478
|
142
|
118
|
0,02596
|
10
|
|
|
0,26483
|
498
|
412
|
0.26895
|
101
|
|
|
1,88679
|
- 3494
|
- 2893
|
1.85786
|
700
|
|
|
0,00620
|
36
|
30
|
0.0065
|
2,45
|
|
|
0,53246
|
1024
|
848
|
0.54094
|
204
|
|
|
? ???? c??????b??????: c = 1
??
|
1
700
|
= 1,4 * 10-3, ce qui permettra de ne pas avoir un
changement
|
brusque du rayon et de fixer la vitesse de parcours.
33
Une brève explication de l'obtention des valeurs du
tableau :
? les colonnes (1) et (2) viennent des abaques et se transcrivent
sans aucune modification ;
? la colonne (3) se calcul : ? * k ? ???????? ?? ? 255 * 0,828
211 ;
??
? la colonne (4) : colonne (1) + colonne (3) ; exemple pour ??
??
0,003285
+ 0,000211
0,003496
? le paramètre de la clothoïde A se calcul : ?? = ??
?? = 700
1,85786 376,8.
La justification des valeurs: ?? = 0,07 * ?? = 0,07 * 700 = 49
?? ne repond pas à la condition ?? = 30 ??
|
L
Alors :E
|
231
=
49
|
= 4,7 5 ? Pour trouver une valeur entière comme multiple
des lignes lors
|
de l'implantation, il convient de faire :540
6 = 90.
Le calcul des points d'implantation (X ; Y) de la
clothoïde réelle suit la logique de lecture dans les abaques, des
valeurs (x ; y) de la clothoïde unitaire des lignes multiples de 90
à 540, qu'on multiplie par le paramètre A (376,8) comme
montré dans le tableau 4.
Tableau 4 : implantation de la clothoïde réelle
|
Lignes
|
x
|
y
|
X
|
Y
|
|
0
|
0
|
0
|
0
|
0
|
|
90
|
0,09000
|
0,00012
|
33,912
|
0,045216
|
|
180
|
0,18000
|
0,00097
|
67,824
|
0,365496
|
|
270
|
0,26996
|
0,00328
|
101,72093
|
1,235904
|
|
360
|
0,35985
|
0,00777
|
135,59148
|
2,927736
|
|
450
|
0,44954
|
0,01518
|
169,38667
|
5,719824
|
|
531,72
|
0,53715
|
0,02596
|
202,39812
|
9,781728
|
|
540
|
0,53885
|
0,02620
|
203,03868
|
9,87216
|
Les coordonnées (X ; Y) ainsi trouvées serviront
au raccordement de l'axe principal de la clothoïde.
Les exigences de stabilité et de visibilité sont
satisfaites par la valeur suffisamment grande du rayon qui est de 700 m.
34
Il faudra lors de l'implantation, piqueter les points
signalés en bleu sur la figure. Le pas étant
|
L
de e = 6
|
231
=
6
|
38 m entre les points.
|
CLOTHOÏDE
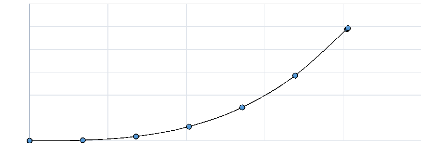
Y en m
12
10
4
8
6
0
2
0 50 100 150 200 250
X en m
Tableau 5 : traçage de la clothoïde par Excel
Il ne s'agit que d'une partie du raccordement de la courbe
qu'illustre la figure ci-dessus et dont le point extrême (203 ; 9,9) est
l'origine de la seconde clothoïde. Cette dernière ne sera qu'une
continuité de la première par changement du
référentiel lors de l'implantation.
|
|



