4) Estimation
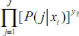
Le logit multinomial/conditionnel s'estime par la
méthode du maximum de vraisemblance. La vraisemblance du modèle
s'écrit de la manière suivante. D'abord, la probabilité
que l'individu i, étant donné ses
caractéristiques et celles des différents choix offerts, fasse le
choix j est égale à :
Où, rappelons- le, yij = 1 si i a
choisi j, 0 sinon. C'est la contribution de i à la
vraisemblance. Ensuite, en supposant que chaque individu a fait un choix
indépendamment des choix effectués par les autres, la
probabilité que les n individus de l'échantillon aient
fait les choix observés est le produit des probabilités :
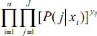
37
En prenant le logarithme de cette quantité, le log
-vraisemblance est finalement égale à :
Ensuite, la transformation de variable dépendante en
une fonction de probabilité, est due par le fait que la valeur
prédite doit donc se situer entre 0 et1.
Cette log -vraisemblance dépend des paramètres
de la forme fonctionnelle de P (j/xi). Une propriété
générale du maximum de vraisemblance est que, sous réserve
que P (j/xi) soit
correctement spécifiée, maximisant est un
estimateur convergent de .
Dans un modèle multinomial, la part observée des
individus appartenant à la catégorie j est égale à
la moyenne empirique des probabilités prédites d'appartenance des
individus à la catégorie j. En ce sens, le modèle
prédit exactement la répartition des individus par
catégorie.
? Spécification du model à
estimer
En nous servant du modèle empirique de logit
multinomial, nous cherchons à estimer la performance par l'atteint de
l'objectif sur trois plans, à savoir :
1. Sur le plan social,
2. Sur le plan économique,
3. Sur tous les deux plans.
Le choix de la catégorie de référence
étant arbitraire nous décidons ici que, celle qui va nous servir
à la comparaison est l'atteinte de l'objectif sur les deux plans, (j=3).
Ceci nous permet à décomposer le modèle selon le type de
l'objectif que nous voulons atteindre parce que la conséquence de cela
est que le modèle cherche à mesurer l'effet d'une variable
explicative sur le rapport entre la probabilité d'atteindre la
performance sur le plan déterminé et la probabilité
d'atteindre la performance sur le plan de référence.
- Nous aurons pour le premier plan : ln
[P(j=1)/P(j=3)]= âj0 + âj1FC + âj2AI+ âj3DI+
âj4TI+ âj5IPD+ âj6MI.
- Pour le deuxième plan nous avons : ln [P
(j=2) / P (j=3)] = âj0 + âj1FC+ âj2AI+ âj3DI +
âj4TI+ âj5IPD+ âj6MI.
38
A priori, trois types de variables peuvent figurer dans la liste
des explicatives :
· Des variables continues ;
· Des variables binaires ;
· Des variables qualitatives ayant plus de deux
modalités.
Les premières ne posent pas de problème
particulier. On peut traiter les variables binaires comme des variables
continues à condition de les coder en 0 et 1. En revanche, les variables
qualitatives ayant plus de deux modalités doivent recevoir un traitement
particulier. Plus précisément, une variable, dont les
modalités sont 1, 2, ..., M, sera remplacée par M variables
binaires : la mième vaut 1 si l'individu a la
modalité m, 0 si non. Ces M variables binaires sont colinéaires
puisque leur somme vaut toujours 1. Comme avec tout autre modèle
économétrique (modèle linéaire ou autre) il faut
alors en exclure une du modèle, sinon les paramètres qui leur
sont attachés ne pourraient être estimés. La
modalité exclue est appelée modalité de
référence de la variable explicative. Selon que les
variables sont continues, binaires ou polytomiques, les paramètres du
modèle n'ont pas la même interprétation, et on ne calcule
pas de la même manière les effets des variables sur les
probabilités d'appartenance aux différentes catégories.
| 


