Comment le cadre théorique de la problématisation dans le paradigme de l'enseignement par compétences peut éclairer sur le processus engagé par un élève de lycée professionnel dans sa résolution d'un problème mathématiques

ANNEXE 3 :

GRILLE DETAILLEE DES COMPETENCES

Conçue par l'auteure de cette recherche et distribuée aux élèves en début de formation

Inspirée du manuel scolaire Mathématiques CAP groupement A et Editions Foucher, 2016, pp.5 et 6.

Durant chaque évaluation, le professeur analyse votre travail à travers 5 compétences : s'approprier, analyser/raisonner, réaliser, valider, communiquer.

Quel est le sens de ces verbes? Quel est le travail attendu? Comment s'y prendre?

Voici quelques conseils et explications pour travailler efficacement.

ATTITUDES (savoir-être) : c'est une prédisposition à l'action indispensable pour s'engager dans le travail

Le sens de l'observation

La curiosité, l'imagination raisonnée, la créativité, l'ouverture d'esprit

L'ouverture à la communication, au dialogue et au débat argumenté

Le goût de chercher et de raisonner

La rigueur et la précision ; l'esprit critique vis-à-vis de l'information disponible

La persévérance

L'esprit critique vis-à-vis de l'information disponible

COMPETENCES : capacité à mobiliser et à réinvestir des connaissances, des capacités et des attitudes afin d'atteindre un objectif donné dans une situation de résolution d'un problème

Que doit faire l'élève?

Qu'attend le professeur?

S'APPROPRIER

ANALYSER RAISONNER

REALISER

VALIDER

Prendre connaissance de la situation et la comprendre

Bien lire la situation et la problématique

Repérer les informations qui semblent utiles, en les surlignant par exemple

S'interroger : Quel est le problème? Que cherche-t-on? Indications des données ou informations recensées

Classement des informations si cela est demandé ou nécessaire

Eventuellement explication orale de ce qu'il faut chercher

Proposer une méthode de résolution ou faire une proposition de réponse avec les éléments à disposition

Lire avec attention la consigne qui donne des indications sur les hypothèses à émettre :

- Émettre des conjectures, formuler des hypothèses.

- Proposer une méthode de résolution. - Élaborer un algorithme.

Choisir, élaborer un protocole. Proposition de méthode de résolution en nommant les outils mathématiques à utiliser

Formulation d'une proposition qui permet de répondre à la question posée

Détail des étapes de la méthode de résolution

Effectuer des calculs, lire un graphique, utiliser une simulation
	Mettre en oeuvre une démarche validée par le professeur Effectuer les calculs nécessaires en étant très attentif (pour éviter faute de frappe...)		L'unité de mesure et/ou les symboles sont indiqués Toutes les étapes des calculs sont indiquées
	Utiliser la simulation informatique si elle est proposée ou si elle parait pertinente dans la recherche		Les calculs sont justifiés par une formule, une propriété...

Vérifier la vraisemblance des résultats ou indiquer si une proposition de réponse est vraie ou fausse

Rendre compte d'une démarche, d'un résultat à l'écrit ou à l'oral

Comparer les résultats avec les données et/ou informations recueillies pour en vérifier la cohérence

Vérifier si l'ordre de grandeur des résultats semble possible

Analyser les résultats trouvés aux différentes questions et réfléchir à leur utilisation pour répondre à la problématique

COMMUNIQUER

Bien s'assurer de répondre à la question posée

Organiser ses réponses

Réfléchir à bien justifier ses réponses Validation (ou non) de la proposition de réponse de départ

Justification des conclusions en utilisant les résultats et/ou les données

Rédaction d'une conclusion qui répond bien à la problématique de départ

Utilisation d'un vocabulaire mathématique adapté

Présentation d'un travail soigné, clarté de l'expression (orale et/ou écrite)

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[96]

ANNEXE 4 :

Documents de préparation de l'enseignante pour la mise en oeuvre de l'activité « grains de riz »

INVESTIGATION grains de riz : mise en oeuvre Document prof

Séance 1 :

5 min : En vidéo projection l'énoncé de l'investigation1.

Distribution du document 1 « recherche individuelle investigation ».

15 min : Les élèves seuls

- Cherchent à s'approprier la situation

- Doivent produire une trace écrite « brouillon » des questions qu'ils se posent, des

éléments dont ils disposent pour cette appropriation et la compréhension de ce qui est demandé...

- Envisagent une méthode de résolution (trace écrite de leur(s) recherche(s)).
Le document 1 « recherche individuelle investigation » est ramassé.

10 min : Synthèse collective des recherches individuelles, discutions, débat sur les méthodes engagées... Distribution du document 2 « protocole de résolution envisagé _ investigation ».

5 min : Constitution de groupes de travail.

15 min : Mise en commun par groupes des réflexions individuelles.

Sur le document 2 distribué « protocole de résolution envisagé _ investigation », chaque élève du groupe doit, après concertation avec les autres du groupe, o rédiger à l'écrit la démarche de résolution engagée (sur doc.2 « protocole de résolution envisagé _ investigation ») afin d'être « opérationnels » à la séance suivante pour la réalisation de leur protocole et la résolution du problème avec rédaction du compte rendu.

- Lister l'ensemble des ressources dont le groupe aura besoin (ordinateur, calculatrice, ...) Le document 2 « recherche individuelle investigation » est ramassé.

Séance 2 :

Distribution du document 3 « compte rendu de la résolution du problème d'investigation ». Il sera ramassé en fin de séance.

Les documents supports ramassés séance 1, sont distribués nominativement aux élèves : Doc.1

« recherche individuelle investigation » et Doc.2 « protocole de résolution envisagé »

55 min : Les élèves reconstituent les groupes de travail mis en place séance 1.

Les ordinateurs sont à disposition (6 ordinateurs pour 18 élèves) et l'enseignant est disponible pour répondre à leurs besoins matériels.

L'enseignant ne répondra à leur question que par des feedbacks afin de guider les élèves dans leur réflexion sans la piloter.

Christelle Brémaud_E179552Q

[97]

INVESTIGATION : éléments de correction Document prof

!!! VIGILANCE RECHERCHE INTERNET : les élèves ne doivent pas ouvrir les pages concernant

la résolution du problème !!!!

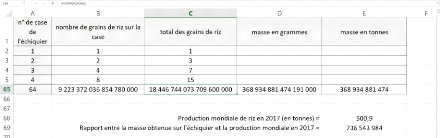
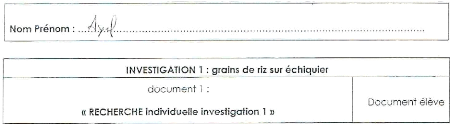
Etape 1 : recherche du nombre total de grains de riz

Utilisation du tableur pour simulation :

Information relevée : nombre de grains de riz = 18 446 744 073 709 600 000

Etape 2 : masse correspondant

Ressource 1 :

https://www.ilephysique.net/sujet-masse-d-un-grain-de-riz-190277.html Information relevée : Un grain de Riz a une masse de 0.020 g

Calcul de la masse totale de grains de riz obtenus :

0.020 * 18 446 744 073 709 600 000 = 368 934 881 474 191 000 grammes
= 368 934 881 474 tonnes

Etape 3 : recherche d'éléments de comparaison pour répondre à la problématique Ressource 2 : http://www.fao.org/worldfoodsituation/csdb/fr/

Site de l'organisation des Nations Unies pour l'alimentation et l'agriculture (Food and Agriculture Organization of the United Nations).

Information relevée : Production mondiale de riz en 2017 = 500.9 tonnes

Etape 4 : interprétation et conclusion

Calcul du rapport entre la masse obtenue sur l'échiquier et la production mondiale en 2017 = 368 934 881 474 / 500.9 = 736 543 984

Christelle Brémaud_E179552Q

[98]

INVESTIGATION grains de riz: SCENARIO A PRIORI et éléments de correction				Document prof
compétences	capacités	observable durant l'action de l'élève	Attendus
s'approprier	rechercher, extraire et organiser l'information	comprendre l'énoncé du problème se mobiliser en cohérence avec les consignes données, reconnaître et relever des données utiles pour répondre au problème organiser les données dans un tableau/faire un schéma	1 grain de riz pour la première case de l'échiquier, 2 pour la deuxième et ainsi de suite, le nombre de grains étant doublé d'une case à l'autre.
analyser	émettre une conjecture	formuler une hypothèse ou une conjecture, proposer une modélisation concernant la réponse au problème	pour pouvoir répondre à la question "requête réalisable?" on cherche si - le calcul est possible pour connaitre le nombre total de grains de riz - si le résultat éventuel a du sens
analyser	émettre une conjecture, proposer une méthode de résolution	proposer une méthode, en définir les étapes principales et la justifier pour valider l'hypothèse, la conjecture ou répondre au problème identifier les paramètres pertinents	il y a 63 calculs (64 résultats en partant de 1) à effectuer les uns après les autres, le résultat étant le produit par 2 du résultat précédent en partant de 1 (le nombre de grains dans la case 1)
			il faudra comparer la somme de ces 64 résultats obtenus à une donnée qui a du sens (production mondiale de riz en 2017)
			on utilise un tableur avec - colonne A les n° de cases de 1 à 64, - colonne B, en Bn les produits par 2 du résultat précédent en Bn-1, avec en B1 la valeur de départ 1, - en B65 le résultat de la somme des 64 résultats intermédiaires pour le nombre total de grains.
réaliser	choisir une méthode de résolution	choisir et mener à bien une méthode mathématique	apparait le nombre de grains de riz sur chaque case
			apparait le nombre de grains de riz total avec - le calcul "=SOMME(B1:B64)" - le résultat (= 18 446 744 073 709 600 000)
s'approprier	rechercher l'informatio n	reconnaître et relever (trouver) des données utiles pour répondre au problème	avec masse d'un grain de riz = 0,020 g
analyser	proposer une méthode de résolution	identifier les paramètres pertinents	détail du calcul pour obtenir la masse totale des grains de riz 0,020×18 446 744 073 709 600 000

[99]

réaliser	exécuter une méthode de résolution	calculer	masse totale des grains de riz = 368 934 881 474 191 000 (grammes)
communiquer	rendre compte d'un résultat	utiliser un vocabulaire adapté, précis (ici les unités de mesure sont précisées et correctes)	en grammes
s'approprier	rechercher l'information	reconnaître et relever (trouver) des données utiles pour répondre au problème	Production mondiale de riz en 2017 = 500,3 millions de tonnes
Analyser.	proposer une méthode de résolution	identifier les paramètres pertinents	conversion en tonnes de la masse totale de riz trouvée = 368 934 881 474 tonnes
		identifier les paramètres pertinents	comparaison des deux masses, 368 934 881 474 / 500 300 000 = 737
s'approprier	Extraire l'information	traduire une observation	interprétation du quotient des 2 masses (justification de la conclusion)
valider	contrôler la vraisemblance d'une hypothèse	prendre une décision à partir de résultats obtenus	conclusion: la requête n'est pas réalisable

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[100]

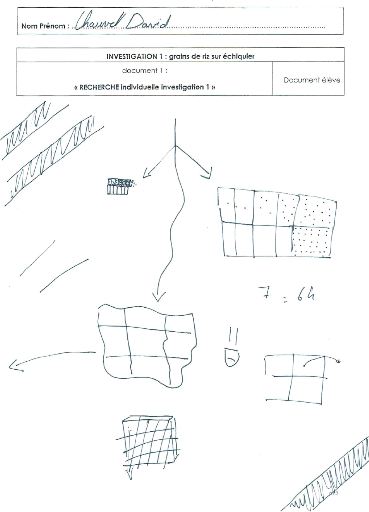
ANNEXE 5 :

Relevés de TRACES ECRITES pour la résolution de la situation-problème RECHERCHE INDIVIDUELLE_ phase 1

Christelle Brémaud_E179552Q

[101]

[102]

Nom Prénom : `

INVESTIGATION 1 : grains de riz sur échiquier

document 1

Document élève

cc RECHERCHE individuelle investigation 1 n

t

t

Lat

Qat ,te pla Q cat .l^- Cc>i d ch Îta

ca c. L! ci ds .-64A Cf c ?r C .

I' ~

_,3 L.04 A0_

}w:S -( c`i-! c0, dee{ f fvi oti. -rev f ) _ 3

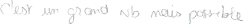
Christelle Brémaud E179552Q

[103]

Christelle Brémaud_E179552Q

[ 104]

tI

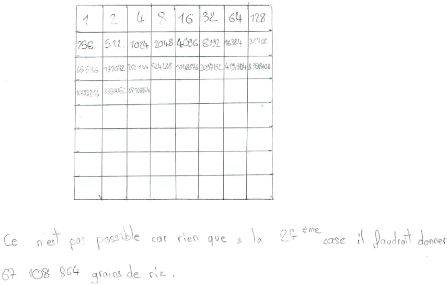
Nom Prénom :

a

INVESTIGATION 1 : grains de riz sur échiquier

document 1 :

Document élève

u RECHERCHE individuelle investigation 1 »

4,34^\

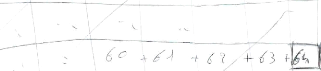
Christelle Brémaud E179552Q

P.3

[105]

Christelle Brémaud_E179552Q

Christelle Brémaud E179552Q

[106]

Nom Prénom : ⁶⁷ Yom--

INVESTIGATION 1 : grains de riz sur échiquier

document 1 :

Document élève

rr RECHERCHE individuelle investigation 1 n

e,,`,Z c3

c	,)		)	-s&	co	i8d	z3
Sig.	loZL;	if..I	)109c	8iyz	aiseh

cw.

[107]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[108]

Christelle Brémaud_E179552Q

[109]

Christelle Brémaud_E179552Q

[110]

Christelle Brémaud_E179552Q

[111]

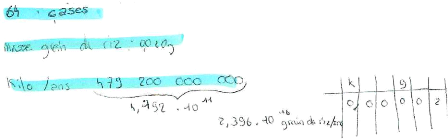
[112]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[113]

ANNEXE 6 : TRANSCRIPTION synthèse de classe_ phase 2 APPROPRIATION DE LA SITUATION PROBLEME grains de riz
Tour de parole	intervenant	intervention
1	Enseignant stagiaire ES	Vous avez aussi le droit de noter euh là où vous hésitez, ce que vous ne comprenez pas. Si ça vous avez besoin de le mettre, n'hésitez pas aussi à le mettre.
2		Tu doubles
3		...
4		Moi je ne comprends pas
5	ES	Bah tu expliques pourquoi.... ce que tu ne comprends pas
6		...
7	Romain	On ne la rend pas comme ça
8	Dorian	Oh là toutes les cases, tu ne t'es pas embêté !
9	Maxime	Bah c'est un damier blanc
10	Elsa	Bah non après faut additionner toutes les cases
11	Evan	Bah non, faut pas additionner toutes les cases
12	Elsa	Bah si parce qu'il faut savoir combien de grains de riz... après faut savoir...
13	Enseignante Ens.	Attention c'est une recherche qui se veut personnelle pour l'instant, vous aurez l'occasion après de mettre en commun. D'accord ?
14	ES	Temps écoulé, on va ramasser vos feuilles
15	Elsa	Faudrait quand même que je fasse...
16	Evan	Tout ça ? Je ne sers à rien dans la vie !
17	Ens.	Je vous ramasse votre feuille ?... s'il y a du recto verso, faites une petite flèche.
18		...
19	ES	Alors ? ... il en ressort quoi de tout ça ?
20	Evan	2080
21	Romain	Il n'y aura pas assez de grains
22	Maxime	(Tout bas à son voisinage) Bon bah c'est 2 puissance 64
23	Ens.	Vous levez la main pour prendre la parole, ce serait parfait et vous essayez de ne pas parler à deux en même temps
24	Elsa	(tout bas en réponse à Maxime) Bah non, bah non, c'est 2 plus 2 puissance 3 plus 2 puissance 3....
25	Romain	Il n'y aura jamais assez de grains
26	ES (note)	Il n'y aura jamais assez de grains
27	Dorian	Bah, Ça dépend du nombre de grains qu'il a
28	Elsa	Bah non, s'il réunit toutes les rizicultures
29		Il n'y aura jamais assez de place
30	ES	Il n'y aura jamais assez de grains
31	Maxime	Il ne va jamais compter...
32	Evan	Il n'y a pas assez de place
33	Maxime	... même pour euh
34	ES (note)	Il n'y a pas assez de place
35	Elsa	Bah ça dépend de l'échiquier ! Tout dépend de l'échiquier...
36	Maxime	La taille de l'échiquier... l'échelle de l'échiquier. Donc il ne va pas s'amuser à compter un million de grains de riz non plus quoi !
37	ES (note)	Tout dépend de l'échiquier
38	Elsa	En pas mal de temps quoi !

Christelle Brémaud_E179552Q

[114]

39	ES	Ça met du temps
40	Elsa	.... C'est possible... c'est possible mais il va passer pas mal de temps !
41		(inaudible)
42	Inès	C'est clair
43	David	... mais c'est le souverain... (inaudible)
44	ES (note)	Ça met du temps mais c'est possible... que peut-on rajouter ?
45	Coralie	On n'a jamais dit qu'il fallait les poser sur le cadre
46	ES	(Relecture à voix haute de l'énoncé) ...de lui donner un grain pour la première case de l'échiquier, 2 pour la deuxième, et ainsi de suite, et on ne demande jamais de le poser
47		... (inaudible)
48	Erwan	C'est pas marqué !
49	David	Voilà... en gros c'est obligé !
50	ES	Est-ce qu'on peut rajouter autre chose... rien d'autre ?...
51	Elsa	(tout bas à ses voisins) 2 puissance 4 pfffff
52	ES	Alors qui n'a pas compris l'énoncé dans ce cas-là ?!... allez, on n'hésite pas hein !
53	Inès	Bah il n'est pas détaillé, alors !
54	ES	Euh non mais... (inaudible)
55	Inès	Ah nan... mais moi je...
56	ES	Alors il n'y a qu'une seule personne qui n'a pas compris, donc tous les autres sont capables de résoudre le problème d'un seul coup ?
57		Ouais
58		Non
59	Elsa	Bah avec les puissances !
60	David	Ca on peut le dire avec un dessin
61	ES	Bon alors, où est-ce que ça butte ? où est-ce que vous ne comprenez pas
62	Dorian	Bah, on n'a juste pas assez de ..... On n'a pas assez d'informations
63	Maxime	Il n'y a pas assez d'informations
64	ES (note)	Il n'y a pas assez d'informations
65	Evan	Ouais
66	Elsa	Bah si !
67	Dorian	(A Elsa) Non parce que tu peux connaître le nombre de grains de riz, mais tu seras incapable de dire s'il y en a assez ou pas.
68	Evan	Ah oui !
69	Maxime	Bah on peut trouver le nombre de grains de riz qu'il faut mais on ne peut pas savoir si... il est assez énorme
70	Ens.	Ce serait bien que tout le monde s'écoute !... tu peux redire Maxime
71	Maxime	On peut réussir à connaître le nombre de grains de riz qu'il faut mais on sait pas après s'il y en a assez ou pas
72	Erwan	Bah si !
73	Elsa	Le roi on ne sait pas ce qu'il est capable de fournir
74	Dorian	Est-ce qu'il est capable de fournir ?... oh bah dis donc c'est français ça !
75	Maxime	(à son voisin) C'est le souverain qui donne des grains de riz
76	Dorian	(à Maxime) oui oui
77		La taille de l'échiquier
78	ES (note)	Alors... On ne connait pas la quantité de riz...
79	Dorian	que possède le souverain
80	ES	... dont dispose le souverain
81	ES	Qu'est-ce qui nous manque comme donnée ?
82	David	De quoi ?
83	ES	Vous avez dit qu'il n'y avait pas assez d'informations... est-ce que c'est la seule info qui nous manque ?

Christelle Brémaud_E179552Q

[115]

84	David	Est-ce que, non... est-ce que les grains de riz doivent rester absolument sur les cases ou euh
85		Non !
86	ES	On a déjà posé la question... on ne demande jamais de poser les grains de riz sur l'échiquier...
87	David	Vous n'avez pas de réponse alors
88	ES	je n'ai pas de réponse là-dessus non
89	Ens.	Est-ce que c'est écrit ? Quelqu'un a dit tout à l'heure « ce n'est pas écrit »
90	David	Bah oui
91	Romain	Ce qui n'est pas écrit n'est pas écrit
92	David	Bah c'est obligatoirement possible
93	Ens.	Qu'est-ce qui est obligatoirement possible ?
94	David	Que chaque case, on peut toujours doubler si on n'a pas de contrainte...ça nous fait zéro contrainte
95	Ens.	Tu en as des contraintes mais pas celles-ci
96		(rire d'un élève)
97	David	Ah bon !?... parce que j'en vois pas
98	Ens.	Au pire
100	David	Au pire on le fait à la calculette
101	Ens.	.. et comment tu vas faire avec la calculette ?
102	Elsa	Avec les puissances !
103	Ens.	Avec les puissances... c'est toutes ces questions-là qu'il faut que vous vous posiez
104	Elsa	(en même temps que l'Ens.) 2 puiss...1... plus 2 puissance 2 plus de 2 puissance 3
105	Ens.	C'est avec toutes ces questions-là que vous allez réussir à arriver à la solution... est-ce qu'il n'y a que la calculatrice ? Vous avez peut-être d'autres outils à disposition
106	Elsa	Bah les tableurs
107	Ens.	Les tableurs... vous pouvez tout imaginer... comment vous allez chercher à résoudre ce problème-là pour pouvoir y répondre ... et est-ce que la solution à laquelle vous allez arriver elle est plausible ? parce que l'idée c'est que « est-ce que la requête est réalisable ? » c'est-à-dire est-ce que la réponse à laquelle vous allez arriver est plausible ?... Au regard de quoi ?
108	Elsa	Bah du temps passé quoi!
109	Ens.	Et peut-être d'autres informations dont vous ne disposez pas, que vous allez avoir à aller chercher... pour comparer votre résultat à des données
110	Maxime	De toute façon, il n'arrivera jamais à compter exactement tout le nombre des grains de riz
111	Ens.	Je n'ai pas entendu Maxime
112	Maxime	Il n'arrivera jamais à compter exactement le nombre de grains de riz qu'il a
113	Ens.	Ah bah le but, si on vous donne ça c'est qu'il y a quand même une possibilité d'y arriver !
114		(Brouhaha)
115	Ens.	Est-ce que c'est réalisable ça ne veut pas dire que vous n'allez pas réussir à obtenir une réponse
116	Elsa	Ah !
117	Ens.	parce que le but du jeu, parce qu'on n'est pas pervers quand même, c'est que vous êtes censés pouvoir obtenir une réponse... maintenant pour savoir si c'est réalisable il va falloir que vous mettiez votre réponse au regard de certaines données que vous irez chercher... qui vous semblent pertinentes... pour pouvoir comparer et valider du coup la chose

Christelle Brémaud_E179552Q

[116]