III.2. ESTIMATION DES PARAMETRES DU MODELE.
Rappelons que le modèle est spécifié sur
données chronologiques allant de 2007 à 2012. Par ailleurs, la
Méthode des Moindres Carrés Ordinaires ne fournit des
éstimateurs fiables et/ ou efficaces que lorsqu'un corpus
d'hypothèses sur lequel elle est bâtie est vérifiée.
Ainsi, les hypothèses suivantes doivent impérativement être
vérifiées :
H1 :E(  )=0 ; l'espérance mathématique du
terme aléatoire est nulle. En moyenne, le modèle est bien
spécifié et donc l'erreur moyenne est nulle ;
H2 :
E(?t2)=ó2, la variance de
l'erreur est constante. C'est l'hypothèse
d'homoscédasticité de la variance de l'erreur ;
H 3 : E( 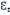 ,   )=0 si t?t' ; les erreurs sont non
corrélées(ou encore indépendantes) : une erreur
à l'instant t n'a pas d'influence sur les erreurs à l'instant
suivant ;
H4 : Cov(Xt,
?t)=0 ; l'erreur est indépendante de la variable
explicative. C'est l'hypothèse d'absence
d'endogénéité,
H5 :Cov(Xi, Xj)=0
Si Xi, est différente de Xj ; la covariance
est nulle entre les variables exogenes ; En d'autres termes, les variables
exogènes ne sont pas liées,c'est l'hypothèse d'absence de
multicolinéarité entre lesvariables exogènes.
III.2.1 Verification des
hypothèses.
Prenons chacune des hypothèses et vérifions de
quelle manière elles pourraient être violées :
La première hypothèse de nullité de
l'espérance mathématique du terme aléatoire constitue une
assertion que l'on ne peut vérifier. Nous allons par conséquent,
considérer qu'elle est vraie ;
La deuxième hypothèse
d'homoscédasticité sera considérée comme
vérifiée car le problème
d'hétéroscédasticité ne se pose que pour les
modèles spécifiés en coupes instantanées
(données transversales) ;
La troisième hypothèse faite sur la relation
entre les erreurs sera testée sur base du test de Durbin-Watson. Pour ce
faire, il faut d'abord estimer les paramètres du modèle par MCO
en admettant que les hypothèses sont vérifiées.
| 
