Reconstruction 3D des objets urbains

II.1 Localisation des structures urbaines :

II.1.1 Segmentation :

II.1.1.1 Approche 1 : Contour non-déformable

II.1.1.1.1. Les operateurs dérivateur'' gradient et Laplacien'' :

a. Les opérateurs dérivateurs du premier ordre : Sobel, Prewitt :

Les étapes de détection des contours par la méthode de gradient sont résumés dans l'organigramme suivant :

Algorithme :

Début

Chargement de l'image IM[i][j]

Lire SobelH

Lire SobelV

Pour i=0 jusqu'à hauteur

Pour j=0 jusqu'à largeur

s1=0 ; s2=0 ; s=0 ;

Pour l=0 jusqu'à 3

Pour m=0 jusqu'à 3

s1=s1+ IM [i-m-1][j-l-1]*SobelH[x][y];

s2=s2+ IM [i-m-1][j-l-1]*SobelV[x][y];

s=;

data[i][j]=s ;

Fin

Fin

if (seuil< data [i][j])

data [i][j]=255;

sinon

data [i][j]=0;

fin

fin

Fin

Détection par le gradient :

En entrer : valeur de Seuil.

1. Première étape : calculer le gradient suivant l'axe vertical de l'image.

(IV.1)

2. Deuxième étape : calculer le gradient de l'image suivant l'axe horizontal.

(IV.2)

3. Troisième étape : calculer la norme de gradient de l'image.

(IV.3)

4. Quatrième étape : Suppression des non-maxima

Si la norme du gradient en un pixel (x,y) est inferieure a la norme du gradient d'un de ses 2 voisins le long de la direction du gradient, alors mettre la norme pour le pixel (x,y) a zero

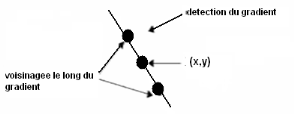
Figure-IV.3 : Etape de suppression des non-maxima

5 - Seuillage des contours (hystérésis)

Utilise deux seuils : un seuil haut (Sh) et un seuil bas (Sb)

Pour chaque pixel de la norme du gradient :

ï Si norme(x,y) < Sb, alors le pixel est mis a zéro (non-contour)

ï Si norme(x,y) > Sh, alors le pixel est un contour

ï Si Sb = norme(x,y) = Sh, alors le pixel est un contour s'il est connecté a un autre pixel déjà acceptéé comme contour

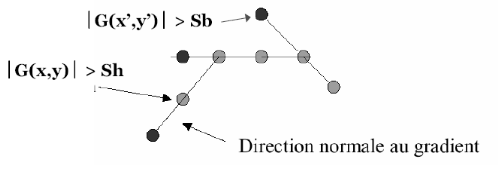
Figure-IV.4 : Etape de seuillage

Résultats obtenu :

Image originale	Détection de contours par l'operateur SOBEL(seuil=136)	Détection de contours par l'operateur PREWITT(seuil=136)

Ces filtres sont moins sensibles au bruit que ceux de Robert car le fait d'introduire un moyenneur local sur le domaine couvert par le masque diminue leur sensibilité au bruit, concernant la qualité du contour, les deux opérateurs fournissent un contour moyen.

b. Les opérateurs dérivateurs de deuxième ordre `' Laplacien'' :

La détection de contours par Laplacien consiste à convoluer l'image par le filtre suivant :

Résultats :

Image originale	Laplacien (seuil = 26)

Figure-IV.4 : Détection de contours par le Laplacien

Remarque : on remarque que L'opérateur de Prewitt se révèle très peu différent de celui de Sobel. On peut toutefois noter qu'il est légèrement plus sensible au bruit, et que : La détection de contours par Laplacien est très sensible aux bruits.

Comparaison des méthodes de détection de contours :

Opérateurs	Sensibilité au bruit	Epaisseur des contours	Localisation	Matrices
Opérateur de Prewitt	peu sensible	épais	centré	3x3
Opérateur de Sobel	Assez sensible	moyen	centré	3x3
Opérateur de Laplacien	Sensible	très fins	centré	3x3

Tab.IV. 1. Tableau comparatif des méthodes de détection de contours.

II.1.1.1.2. Le filtre de Canny:

a. Critères de l'approche de Canny :

- Détection : Bonne détection des points de contours (notamment pour les contours faibles).

- Localisation : Localisation faible des points de contours.

- Unicité de la détection : Pour un contour, on a un seul point de contour.

b. Algorithme de Canny :

Premier étape : appliquer un filtre gaussien c'est-à-dire filtré d'abord l'image avec un filtre gaussien G.

(IV.4)

I' (i, j) =G(x, y)*I (i, j) (IV.5)

Filtre Passe-bas pour enlever le bruit.

Deuxième étape : calculer le gradient en chaque pixel de l'image.

La norme du gradient :

(IV.6)

L'angle du gradient :

(IV.7)

Troisième étape : Approximation de l'angle du gradient à un multiple de 45° pré.

Quatrième étape :

(IV.8)

Alors (IV.9)

Cinquième étape : Seuillage par hystérésis

Soit (S_h , S_b) deux seuils tel que S_h> S_b

> Alors (x, y) point contour ainsi tous les points reliés à (x, y) le long du gradient

> (IV.10)

> (IV.11)

Resultats :

Image originale	L'operateur `'Canny''

Figure II. 5 : Détection de contours par Canny

II.1.1.1.3 Seuillage par hystérésis de l'image gradient :

Algorithme :

Début

Chargement de l'image IM[i][j]

Lire la valeur des seuils (Sh, Sb) ;

Calcul l'image moyenne : moy[i][j] =(R+G+B) /3 ;

Pour (x=0, jusqu'a x<3)

Pour (y=0, jusqu'a y<3)

S1=S1+(moy[i-x-1][j-y-1]*Sobel[x][y]) ;

S2=S2+(moy[i-x-1][j-y-1]*Sobel[x][y]) ;

S= ;

IMA[i][j]=S;

Si (IMA [j][i]< Sb)

IMA[j][i]=0;

Si (IMA [j][i]>Sh)

IMA[i][j]=IM[i][j] ;

Si (IMA [j][i]<Sh & IMA [j][i]>Sb)

IMA[i][j]=IM[i][j] ;

fin

fin

Fin

Résultats obtenus :

Image originale	Exemple1 : Sb=114, sh=145

Figure-II.6 - Seuillage hystérésis

L'opération de seuillage est une étape clé dans le domaine de traitement d'image, elle permet le passage d'une image couleur à une image binaire construite par deux intensités (que du blanc sur les contours, et du noir), mais le problème majeur du seuillage est le choix du seuil qui peut donner meilleur résultat comme il peut donner de mauvais résultat.

II.1.1.2 Approche 2 : Contour déformable

II.1.1.2.1 Les Snakes :

Les contours actifs, ou `'Snake'', permettent de segmenter des images par détection de contours.
Leur utilité est particulièrement bien illustrée en imagerie médicale, les surfaces intéressantes étant en général des formes bien régulières.

L'approche classique consiste à déformer un contour vers le bord de l'objet à détecter, en minimisant une fonctionnelle définie en fonction de l'image et ayant pour effet de régulariser la courbe. Depuis, de nombreuses améliorations ont été apportées au modèle initial. En effet, celui-ci présentait de nombreux inconvénients : sensibilité à l'initialisation, au bruit, réglage difficile des différents paramètres, fausses détections dues à la présence de minima locaux de la fonctionnelle.

Organigramme :

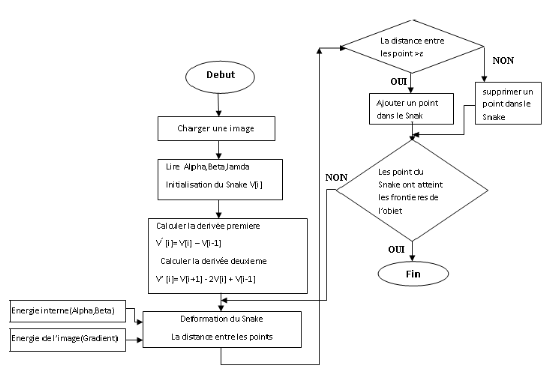
Organigramme IV.3 : Principe du Snake

Nous avons testé la méthode des contours actifs sur des images de zone urbaine avec une haute résolution, sans aucun prétraitement ou amélioration.

Résultats obtenu :

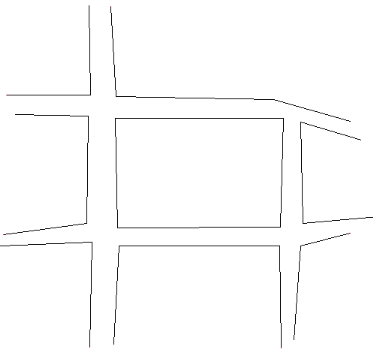
Dans la figure IV.8, nous remarquons que le snake initial a convergé vers la route dans certains cas, dans d'autre, à cause d'une part de l'ombre portée des bâtiments sur la route et d'autre part de l'existence des objets qui occultent la route (voiture, arbre, marquage au sol) il n'a pas convergé vers la route; car ces objets changent la radiométrie de la route dont le snake s'appuie pour optimiser son déplacement.

II.1.1.2.2 Méthode d'ensemble de niveau zéro Level Set :

a. Avec « Arrêt aux bords »

Cette méthode est basée sur la définition d'une fonction (g) appelée `'fonction d'arrêt aux bords'' garantit l'arrêt de l'évolution de la courbe sur les bord de l'objet à détecté.

Début

Charger une image ;

Initialiser par ;

Pour chaque itération faire 

Pour (x,y) faire

Calculer g () ;

Calcular FA ;

Calcular FG ;

Fin

Calculer  ;

Fin

Fin

Cette méthode est simple à implémenter, mais le problème qui s'impose est que la courbe arrête son évolution sur les premiers bords trouver, donc on a un problème de changement de topologie.

b. Sans « arrêt aux bords » :

Algorithme :

Début

Initialisation de par, n=0

Pour un nombre fixe d'itération faire

Calcule de C₁() et C₂(Ø₀)

Calcule le terme de la courbure K

Calcule

Fin

Résultats obtenu :

1. Avec arrêt aux bords :

Initialisation de la courbe

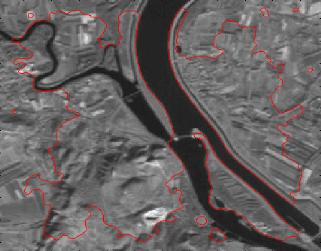
Résultats après 200 itérations Résultats après 1000 itérations

Figure IV.7 Méthode de Level set avec « arrêt aux bords »

2-sans arrêt aux bords :

Initialisation de la courbe

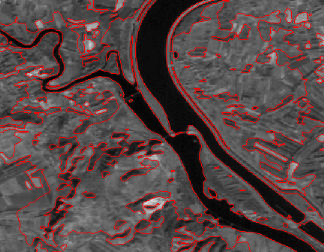
Résultats après 10 itérations Résultats après 200 itérations

Figure IV .8 Méthode de Level set sans « arrêt aux bords »

On remarque que si la courbe initial était au milieu de l'image ?t=0.1, le cycle de réinitialisation est une itération et =0.001x(255)². Après 4 itérations la courbe se stabilise sur les frontières des objets de l'image.

Si on laisse les mêmes conditions, et on change seulement le ?t vers une valeur maximal (5500), après une seule itération on a le même résultat que la première

On remarque aussi, que la méthode avec arrêt au bords donne de bon résultats seulement dans les régions qui ont un gradient élevé. Il faut que la courbe initiale soit proche et complètement contenue à l'intérieur de l'objet. Cette méthode est très lente ; pour faire un changement de topologie il faut initialiser à l'aide de plusieurs courbes.

La deuxième méthode peut détecter les objets dont les bords ne sont pas nécessairement définis par un gradient ; elle permet de faire un changement de topologie à partir d'une seule courbe initiale ; elle est rapide et donne de bon résultats.

D'après les essais précédents, il est claire que la méthode de minimisation d'énergie semble plus éfficace, plus rapide et plus précise que la méthode d'arrêt au bord.

Les objets avec des contours lissés ne peuvent pas être segmenté avec l'approche `'d'arrêt aux bords'', la courbe va éventuellement se rétracter sur elle-même.

Cependant l'initialisation de l'approche de minimisation d'énergie nous permet d'aboutir à la segmentation désirée.

§ Les avantages des LEVEL SETS :

- Prise en compte des changements de topologie automatique.

- Grandeurs géométriques intrinsèques (normales entrante/sortante, courbure) faciles à calculer.

- Extension à la 3D simple : il suffit d'ajouter une coordonnée à l'équation d'évolution de la fonction ö : on a alors un volume ö(x, y, z, t).

- Discrétisation de ö avec une grille définit dans le domaine de l'image.

- Utilisation des méthodes numériques connues pour calculer les dérivées.

§ Les inconvénients des LEVEL SETS :

L'implémentation implique plusieurs problèmes :

- On doit construire une fonction initiale ö(x, y, z, t=0) de manière à ce que son niveau zéro corresponde à la position initiale du contour.

- L'équation d'évolution n'est dérivée qu'au «  Level set zéro » ; la fonction vitesse v n'est donc pas définie(en générale) pour les autres Level sets.

- La déformation constante peut causer la formation de coins saillants sur le modèle initiale lisse. Ce coin peut perturber les déformations successives, Puisque la définition de la normale devient ambiguë. Parfois nécessaire de recalculer la fonction distance par rapport au niveau zéro.

§ comparaison entre les'' Snake'' et'' Level Set'':

Les modèles paramétriques'' Les Snake''

- Représentation explicite des modèles sous leur forme paramétrique pendant la déformation

- Implémentation rapides (temps réel).

- Adaptation à la topologie des objets difficiles.

- Nécessité de réinitialiser les paramètres de la courbe.

Les modèles géométriques'': Les Level-Sets (courbes de niveaux) `'

- Représentation implicite des modèles comme un ensemble de niveaux d'une fonction scalaire de dimension supérieure

- Adaptation à la topologie de ces modèles est automatique

- Modèles utilisant la théorie de l'évolution de courbes ou les Level-Sets (courbes/ensembles de niveaux).

- Les courbes/surfaces évoluent en fonction de mesures géométriques résultant d'une évolution, et donc indépendantes de paramètres.

- Les courbes sont représentées comme un ensemble de niveaux d'une fonction de dimension supérieure.

- Les changements de topologies (fusion, séparation, etc..) sont gérés automatiquement.

- L'évolution de la courbe s'arrête sur les contours de l'objet.

- On étudie l'évolution de la courbe en utilisant uniquement des mesures géométriques (normal, courbure, ...) et non pas des quantités dépendant de paramètres (dérivées d'une courbe spécifique).