4.5.3 Le modèle MF modifié
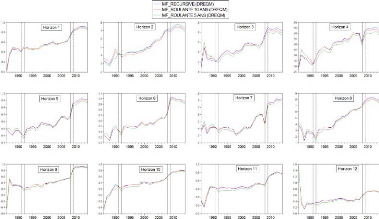
L'oservation des horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de
la figure 4.11 permet de constater que les trois approches appliquées au
modèle MF modifié battent la marche aléatoire. Toutes les
trois séries de ÄREQM affichent des valeurs positives pour ces
horizons. À l'opposé, sur les horizons h= 9, 10, 11, de la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléaoire. Ainsi pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.40. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.47 et -0.019. Enfin pour h=11 de l'année 1987, l'approche
récursive et l'approche roulante 10 ans affichent les valeurs
négatives qui sont respectivement -0.039 et -0.05.
59
Figure 4.11 Séries ÄREQM du
modèle MF modifié par approche et horizon
En considérant les trois approches du modèle MF
modifié, on peut constater que leurs performances relatives sont
similaires, en général. Néanmoins, suivant des
périodes de l'échantillon de prévision, certaines
différences peuvent être notées. Ainsi de janvier 1986
à décembre 1991, l'approche roulante 5 ans est plus performante
que les deux autres approches, au niveau de tous les douze horizons. Pour la
période 19922008 aucun modèle ne domine clairement. Cependant
à partir de 2009, l'approche récursive se montre la plus
performante dans la plupart des horizons sauf les horizons h=10, 11, 12.
Les modèles sont moins performants à court
terme. Cependant à moyen et à long terme, les performances des
modèles s'améliorent avec des courbes qui ont une tendance
générale à la hausse.
60
4.5.4 Le modèle PE modifié
Les trois approches appliquées au modèle PE
modifié battent la marche aléatoire pour les horizons h = 2, 3,
4, 5, 6, 7, 8 et 12 (voir figure 4.12). À ces horizons, toutes les trois
séries de ÄREQM sont positives.
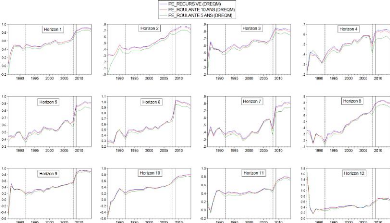
Figure 4.12 Séries ÄREQM du
modèle PE modifié par approche et horizon
Par contre, sur les horizons h= 1, 9, 10, 11, de la
période 1986-1988, le modèle PE modifié ne fait pas mieux
que la marche aléaoire. Ainsi pour h=1, l'approche roulante 5 ans a une
valeur négative de -0.17. Pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.5. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.55 et -0.0036. Enfin pour h=11 de l'année 1987, les trois
approches affichent les valeurs négatives qui oscillent entre -0.068 et
- 0.0064.
61
Les trois approches du modèle PE ont leurs performances
relatives qui sont proches mais avec quelques nuances, suivant des
périodes de l'échantillon de prévision. Ainsi, aucune
approche ne s'impose clairement sur la totalité des douze horizons.
Cependant de 1992 à 2008, on note que l'approche récursive fait
légèrement mieux que les deux autres approche. De 2009 à
2014, l'approche récursive performe nettement mieux sur les horizons 1
à 8, mais légèrement mieux sur les horizons 9 à
12.
Les modèles sont moins performants à court
terme. Cependant à moyen et à long terme, les performances des
modèles s'améliorent avec des courbes qui ont une tendance
générale à la hausse. On note toutefois une exception au
niveau de l'horizon h=12 où la période 1986-1988 est
marquée par une forte décroissance des valeurs des
séries.
Au terme des sous- sections précédentes
consacrées à l'étude par horizon des modèles POTI,
PPA, MF, PE modifiés, sur la base du critère ÄREQM, nous
remarquons que les allures des séries issues des modèles sont
similaires, en général. Cependant, on note quelques
différences qui sont les suivantes :
- pour les horizons de 1 à 8 et l'horizon 12, les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
- les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
- sur la période 1986-1991, la meilleure approche est
l'approche roulante 5 ans appliquée aux modèles POTI, PPA, MF
modifiés. Cette approche fait mieux que les approches roulante 5 ans et
roulante 10 ans, pour les douze horizons.
62
- sur la période 1992-2014, c'est l'approche
récursive qui performe plus que les approches roulante 5 ans et roulante
10 ans.
Dans la sous-section qui suit, nous rechercherons selon le
critère ÄREQM, sur la période 1986-1991, le meilleur
modèle pour l'approche roulante 5 ans. Ensuite pour la période
1992-2014, nous rechercherons cette fois-là, le meilleur modèle
pour l'approche récursive.
4.5.5 Les meilleurs modèles selon le
critère ÄREQM
4.5.5.1 Le meilleur modèle pour la
période 1986-1991
La figure 4.13 affiche les séries de la statistique
ÄREQM obtenues avec le VAR et l'approche roulante 5 ans appliquée
aux modèles que sont MF, POTI, PPA, PE modifiés. La
période de comparaison est de janvier 1986 à décembre
1991, pour les douze horizons de prévision. Il y a premièrement
le modèle MF modifié qui se distingue par ses meilleures
performances prévisionnelles. Il est suivi par le modèle POTI
modifié.
63
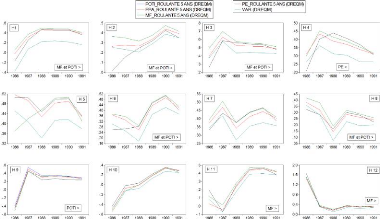
Figure 4.13 Séries ÄREQM :
l'approche roulante 5 ans par modèle (1986-1991)
En effet sur les horizons h = 1, 2, 3, 6 et 8, les
modèles MF et POTI modifiés ont les mêmes performances et y
sont simultanément les plus performants. En plus le modèle MF
domine seul sur les horizons 11 et 12 tandis que le modèle POTI
modifié domine seul l'horizon 9.
Au total, pour la période initiale (1986-1991) de
l'échantillon de prévision, le meilleur modèle est le
modèle MF modifié auquel est aplliquée l'approche roulante
5 ans. Il est plus performant que tous les autres modèles car il les
domine sur 7 horizons, h= 1, 2, 3, 6, 8, 11, et 12. Sur ces horizons, le
modèle MF modifié obtient les plus grandes valeurs de
ÄREQM.
64
Au total, sur l'ensemble de la période 1992-2014, le
meilleur modèle est le modèle MF modifié auquel est
appliquéel'approche récursive.
| 


