4.4.4 Modèle PE modifié
Sur la figure 4.6, les trois séries (récursive,
roulante 5 ans, roulante 10 ans) du modèle PE modifié font mieux
que la marche aléatoire sur les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12.
À ces horizons, on observe des valeurs de U de Theil comprises entre
0.65 et 0.99 sur tout l'échantillon de pévision (1986-2014). Le
modèle PE modifié bat alors la marche aléatoire entre 1%
et35%. Par contre sur les horizons h= 1, 9, 10 et 11, le modèle PE
modifié ne bat pas toujours la marche aléaoire. Ainsi pour h = 1,
la série concernant l'approche roulante 5 ans a une valeur de U de Theil
égale à 1.13 en 1986. Pour h = 9, les trois séries ont des
valeurs avoisinant 1.35 en 1986. Pour h=10, les trois séries ont des
valeurs qui oscillent entre 1.002 et 1.36, dans la période 19861988.
Enfin pour h=11, les trois séries ont des valeurs comprises entre 1.004
et 1.047. Ainsi le modèle PE modifié fait pire que la marche
aléatoire à 0.2%-35%.
- Les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
51
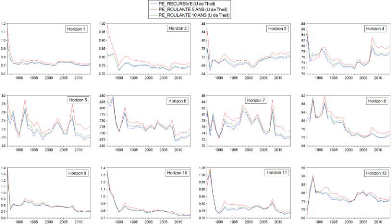
Figure 4.6 Séries U de Theil du
modèle PE modifié par approche et horizon
La comparaison des trois approches sur les périodes de
l'échantillon de prévision nous révèle que leurs
performances relatives sont proches. Toutefois, l'approche récursive
s'avère la plus performante sur les douze horizons durant toute la
durée de l'échantillon de prévision (1986-2014).
Au terme de ces sous-sections, l'étude par horizon des
modèles POTI, PPA, MF et PE modifiés, selon le critère U
de Theil, permet de remarquer que les performances relatives des modèles
étudiés sont proches. Cependant, on note les différences
suivantes :
- pour les horizons de 1 à 8 et l'horizon 12 les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
52
-Pour les modèles POTI, PPA et MF modifiés,
l'approche de prévision roulante 5 ans est la plus performante durant la
période 1989-1991. Quant au modèle PE modifié, sur cette
période (1986-1991), c'est l'approche récursive qui est la plus
performante.
Pour tous les modèles, l'approche récursive est
plus performante que les approches roulante 5 ans et roulante 10 ans pendant la
majeur partie de la période 1992-2014.
Dans la sous-section qui suit, nous recherchons le meilleur
modèle pour la période 1986-1991. Ensuite nous déterminons
le meilleur modèle pour la période 1992-2014.
4.4.5 Les meilleurs modèles selon le
critète U de Theil
4.4.5.1 Le meilleur modèle pour la
période 1986-1991
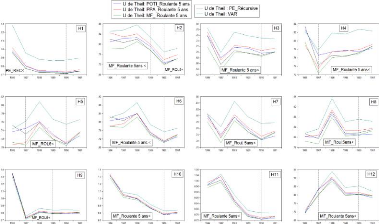
Figure 4.7 Séries U de Theil de
l'approche roulante 5 ans et récursive par modèle
(1986-1991)
53
La figure 4.7 affiche les séries de la statistique U de
Theil obtenues avec l'approche roulante 5 ans appliquée aux trois
modèles que sont MF, POTI, PPA modifiés. Pour le modèle PE
modifié, c'est l'approche récursive qui lui est appliquée.
Le VAR a fait l'objet d'une prévision statique. La période de
comparaison est de janvier 1986 à décembre 1991, pour les douze
horizons de prévision. Le modèle MF modifié se distingue
par ses meilleures performances prévisionnelles. En effet sur les
horizons h = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 et 12 le modèle MF
modifié (avec l'approche roulante 5 ans) est le plus performant. Le
modèle MF modifié auquel est appliquée l'approche roulante
5 ans permet d'avoir les séries U de Theil les plus basses. Les valeurs
de ces séries sont les plus proches de la valeur nulle. Cela signifie
que le modèle MF modifié auquel on applique l'approche roulante 5
ans permet d'avoir les plus faibles erreurs lors des prévisions.
Au total, selon la statistique U de Theil, pour la
période initiale (1986-1991) de l'échantillon de
prévision, le meilleur modèle est le modèle
MFmodifié auquel est appliquée l'approche roulante 5 ans.
| 


