4.4.2 Modèle PPA modifié
Les trois séries (récursive, roulante 5 ans,
roulante 10 ans) du modèle PPA modifié font mieux que la marche
aléatoire sur les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12 (Figure 4.4).
À ces horizons, on observe des valeurs de U de Theil inférieures
à l'unité sur
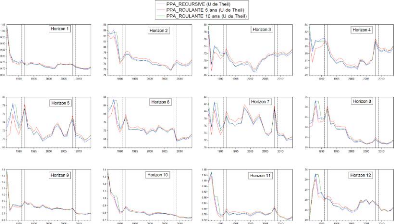
Figure 4.4 Séries U de Theil du
modèle PPA modifié par approche et horizon
47
tout l'échantillon de pévision (1986-2014). Ces
valeurs de U de Theil sont comprises entre 0.67 et 0.93. Cela signifie que de
1986 à 2014 et pour les horizons 2 à 8 et 12, le modèle
PPA modifié bat la marche aléatoire avec un score compris entre
33% et 7%. Toutefois sur les horizons h= 1, 9, 10 et 11, il y a des
années où le modèle PPA modifié ne bat pas la
marche aléaoire . Ainsi pour h= 1 et en 1986, les trois séries de
PPA modifié ont des valeurs autour de 1.02, soit un pire score d'environ
2% par rapport à la marche aléatoire. Pour h=9 et en 1986, les
trois séries ont des valeurs avoisinant 1.35. Cela équivaut
à une mauvaise performance avoisinant 35%, par rapport à la
marche aléatoire. Pour h=10, les trois séries ont des valeurs
oscillant entre 1.007 et 1.36 pendant la période 1986-1989 soit un
mauvais score de 0.7% à 36%. Enfin pour h = 11, les trois séries
ont des valeurs comprises entre 1.03 et 1.06, en 1987. Cela signifie que le
modèle PPA modifié fait pire à hauteur de 3% et 6% par
rapport à la marche aléatoire
48
Les performances relatives des trois approches du
modèle PPA modifié sont proches et varient suivant des
périodes de l'échantillon de prévision. Ainsi de janvier
1986 à décembre 1991, l'approche roulante 5 ans est plus
performante que les deux autres approches, au niveau de tous les douze
horizons. Pour la période 1992-2008, les approches récursive et
roulante 10 ont des performances proches. Toutefois, de l'horizon 5 à
12, l'approche récursive est légèrement la meilleure.
Concernant la période 2009-2014, c'est l'approche récursive qui
se montre la plus performante, pour la plupart des horizons.
4.4.3 Modèle MF modifié
Les trois séries (récursive, roulante 5 ans,
roulante 10 ans) du modèle MF modifié font mieux que la marche
aléatoire sur les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12. À
ces horizons, on observe des valeurs de U de Theil inférieures à
l'unité sur tout l'échantillon de pévision (1986-2014).
Ces valeurs de U de Theil sont comprises entre 0.63 et 0.99. Cela signifie que
de 1986 à 2014 et pour les horizons 1, 2 à 8 et 12, le
modèle MF modifié bat la marche aléatoire avec un score
compris entre 37% et 1%.
49
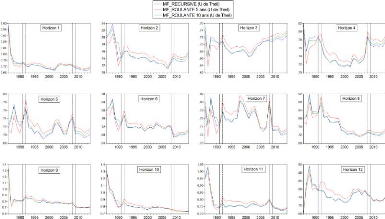
Figure 4.5 Séries U de Theil du
modèle MF modifié par approche et horizon
À l'opposé, sur les horizons h= 9, 10, 11, il y
a des années durant lesquelles le modèle MF modifié
performe moins bien que la marche aléaoire. C'est ainsi que pour h = 9,
les trois séries ont des valeurs avoisinant 1.30 en 1986. Pour h=10, les
trois séries ont des valeurs oscillant entre 1.012 et 1.30 durant les
années 1986, 19987 et 1988. Enfin pour h=11, les deux séries
relatives aux approches récursive et roulante 10 ans affichent
respectivement 1.027 et 1.03. Ainsi, pour les horizons h= 9, 10, 11 et sur la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléatoire à hauteur de 3% à 30%.
Au niveau de la comparaison, on note que les performances
relatives des trois approches sont proches. Cependant, on remarque que pour la
période 1986-1991, l'approche roulante 5 ans a la meilleure performance
sur les douze horizons. Pour les périodes 1992-2008 et 2009-2014, on
note que l'approche récursive du modèle MF modifié fait
mieux que les deux autres approches dans la majorité des horizons.
50
| 


