Reconnaissance des objets polyédriques

1.4 La reconstruction 3D

La reconstruction tridimensionnelle d'un ensemble de points informe sur la structure g'eom'etrique de ce même ensemble.

1.4.1 Les deffirentes approches de la reconstruction tridemensionnelle

· Reconstruction projective

Quand les points sont d'efinis dans un repère projectif. Une telle reconstruction ne contient donc pas d'information critique (absence de la notion d'angle, de longueur, parall'elisme ... ).

FIG. 1.2 - Une reconstruction projective a` droite

· Reconstruction affine

Quand les points sont définis dans un repère affine. Une telle reconstruction contient des informations affines (rapport de longueurs, parallélisme).

FIG. 1.3 - Une reconstruction affine a` droite

· Reconstruction euclidienne

Quand les points sont définis dans un repère euclidien. Cette dernière reconstruction est la plus riche; elle contient les informations que l'homme a l'habitude de manipuler. Nous parlerons dans ce cas de reconstruction euclidienne, car le facteur d'échelle absent ici ne pose pas de problème particulier.

FIG. 1.4 - Une reconstruction euclidienne a` droite

1.5 Techniques de reconstruction 3D

Il existe de nombreuses techniques de reconstruction 3D, On peut répertorier une grande partie des méthodes de reconstruction dans ces quatre catégories :

· Reconstruction a` partir de la texture (Space carving [KUT00]) : Cette méthode basée sur le calcul d'un critère de photoconsistence nécessite d'avoir une lumière constante et homogène tout autour de l'objet.

· Reconstruction a` partir de la géométrie épipolaire[HAR00] : C'est la méthode la plus classique étant donnéqu'on utilise déjàla géométrie épipolaire pour initialiser l'asservissement visuel et que l'on peut estimer les positions des caméras.

· Reconstruction a` partir des contours [BOY97], [LAU95] : Baser la reconstruction 3D sur les contours de l'objet semble être difficilement envisageable sur un objet naturel de forme quelconque avec des contours très irréguliers.

· Reconstruction a` partir du mouvement de la caméra (Factorisation de Tomasi et Kanade) [TRI96].

1.5.1 La vision stéréoscopique

1.5.1.1 Principe

La Vision Stéréoscopique vise a` reconstruire la structure 3D d'une scène. Afin de réaliser cette reconstruction il est nécessaire de connaitre les coordonnées 3D de tous les points d'une scène. La scène est représentée par un couple d'images stéréoscopique. Ces images sont deux représentations de la scène prises sous des angles différents. Chaque point de la scène est projetédans les images de la paire stéréoscopique a` des positions différentes. En vision stéréoscopique pour disposer des coordonnées 3D d'un point il faut disposer des coordonnées de ses deux projections, respectivement dans les images gauches et droites. L'obtention des coordonnées de ces deux projections d'un même point 3D est réalisée gràace a` une phase d'appariement qui vise a` trouver, pour un point donnédans une image,son point correspondant dans l'autre image. Ces deux points sont les projections respectives du même point 3D dans les images droite et gauche.

Le principe de la vision stéréoscopique est résumédans le schéma synoptique de la figure 1.5. Il est a` noter qu'en amont des étapes de la figure 1.5 il est nécessaire de réaliser la calibration du système stéréoscopique de facon a` disposer des paramètres intrinsèques et extrinsèques du système. Ces paramètres seront essentiels dans les phases de rectification et de calcul des positions 3D des points.

La stéréoscopie procède par appariement puis une triangulation

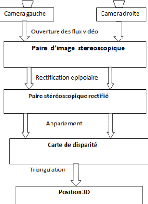
FIG. 1.5 - Synoptique g'en'eral de la vision st'er'eoscopique .

1.5.1.2 L'appariement

Il consiste a` d'eterminer les projections qui se correspondent dans deux images,c'est a` dire quels sont les points 2D repr'esentant les projections d'un même point 3d. Un appariement est donc un n-uplet de points 2D en correspondance

1.5.1.3 La triangulation

C'est une technique d'interpolation de surface, et l'interpolation de surface est le passage du modèle volumique au modèle surfacique. On peut classer la triangulation en deux cat'egories qui sont

· Celle qui s'appuie sur une surface d'efinie implicitement.

· Celle qui s'appuie sur un nuage de points repr'esentant la surface de l'objet

1. La triangulation des surfaces implicites

1. L'algorithme des marching cube

Afin de repr'esenter un volume de donn'ees, on divise ce volume en petits cubes, on fixe un seuil de densit'e par lequel va passer la surface et, a` l'aide des points d'intersection entre les cubes et la surface on polygonise cette dernière et on affiche le r'esultat a` l''ecran. La première difficult'e sous-jacente a` cet algorithme est que, si l'on traite tous les cas de façon s'epar'ee, on a 256 possibilit'es a` traiter (il existe 256 façons qu'une surface courbe peut intersect'e les arêtes d'un cube). Heureusement,

en mettant a` contribution la sym'etrie de rotation on peut r'eduire ce nombre a 23 cas qu'il nous faut traiter s'epar'ement. Dans l'article de Cline et Lorensen [LC87], on parle ici de 14 cas au lieu de 23 car les sym'etries de r'eflexions sont aussi mises a` parti. Cependant, après une 'etude approfondie de la question, il s'est av'er'e que si les symetries de r'eflexion sont utilis'ees des trous ou des inconsistances seront g'en'er'ees dans la surface. Ceci vient du fait que, dans certains cas, la surface se trianguler de façon diff'erente si les sommets du cube qui 'etaient a` l'int'erieur de l'objet passent a` l'ext'erieur et vice-versa. Par exemple si l'on regarde les figures 1.6 et 1.7 qui sont la sym'etrie l'une de l'autre, on peut voir que la surface peut se trianguler de deux façons diff'erentes (les points noirs repr'esentent les sommets du cube a` l'int'erieur de l'objet).

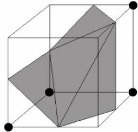
FIG. 1.6 - Une configuration possible d'un cube triangul'e.

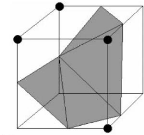
FIG. 1.7 La configuration miroir d'un cube triangul'e.

2. Triangulation a` partir d'un nuage de points

Construction d'un nuage de points pour chaque voxel¹ surfacique en estimant le point par lequel passe la surface,la densit'e du voxel et la normal sont utilis'e pour estimer la position de ce point.

1.5.2 Reconstruction a` partir de géométrie epipolaire

Les principales 'etapes sont repr'esent'ees sur la Figure1.8 .L'extraction de points et l'appariement se font exactement comme pour l'asservissement visuel, a` la diff'erence que l'on travaille sur une s'equence d'images. L''etape de calibration de la paire st'er'eo doit se faire sur des images prises sur le site sans changer les paramètres intrinsèques et extrinsèques des cam'eras. Les paramètres intrinsèques varient en fonction du changement de focale. On utilisera une mire car l'autocalibrage est plus contraignant, n'ecessitant des mouvements sp'ecifiques de la cam'era. On supposera que les paramètres intrinsèques ne varient pas durant toute la phase d'acquisition des images. Une première reconstruction projective est alors r'ealis'ee pour initialiser la suite de la reconstruction, par une m'ethode d'ajustement de faisceaux (Bundle Adjustment).

Ensuite un appariement dense des points appartenant a` la structure est calcul'e a` partir de, paires d'images rectifi'ees (La rectification des images est 'egalement utilis'ee pour l'appariement des points servant a` l'asservissement des cam'eras. Enfin une carte de profondeur dense est calcul'ee pour chaque point appari'e, puis les points 3D sont reli'es entre eux par triangulation (Delaunay). Le plaquage de textures sur les surfaces finit de donner un aspect photo-r'ealiste a` l'objet reconstruit.

Cette m'ethode de reconstruction doit être appliqu'ee sur chaque sous-ensemble de s'equence d'images correspondant a` chaque position du robot autour de l'objet, puis les diff'erentes parties reconstruites sont alors assembl'ees. Il est courant de reconstruire a` partir de sous-ensembles d'images puis de fusionner les modèles partiels ainsi obtenus par une phase d'alignement 3D. Les algorithmes de reconstruction et d'alignement s'appuient sur des correspondances de points ou de droites entre les images. La localisation de ces points ou droites dans les images est affect'ee par un bruit de mesure, influencant la qualit'e des modèles 3D reconstruits.

'Des images 3D sont des images qui représentent une sc`ene en trois dimensions. Le » pixel » est alors appeléun voxel, et représente un volume élémentaire.

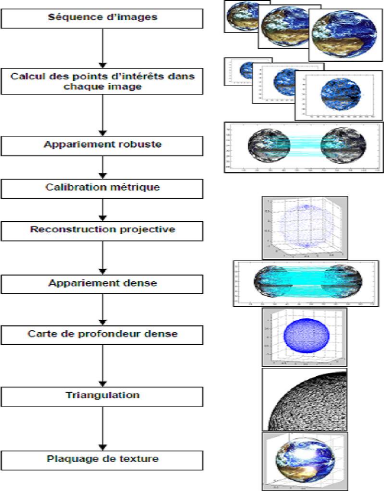
FIG. 1.8 Méthode de reconstruction.

1.5.3 Technique bas'e sur les ombrages ou Shape from shading

Comme son nom l'indique, il s'agit d'extraire une forme a` partir des variations de lumières observées sur la surface d'un objet [ZHA 99], [KOZ 98] au début elle était très peu utilisée dans les systèmes de vision, une des raisons de cet état de fait est l'absence d'algorithmes robustes capables de retrouver les détails fins et discriminants des surfaces des objets (voir figure 1.9). Récemment des études de possibilitéd'utiliser le shape from shading SFS dans la reconnaissance d'objets 3D sont faites [KOZ 98].

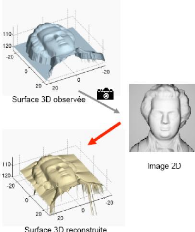
FIG. 1.9 - application de la SFS sur une image 2D.

1.5.4 Repr'esentation par d'etection de d'eformation de formes

Cette approche décrit une nouvelle représentation des formes déformables basées sur des polygones triangulaires (voir figure 1.8), [BAR 98][Cou 2000][Blu 67]elle cherche une structure de correspondance de calibre déformable, o`u on veut trouver une transformation non rigide qui dresse la carte d'un modèle a` une image. Le problème poséest la correspondance de la forme a` l'image, ce dernier est défini en termes d'une fonction d'énergie. Cette fonction d'énergie associe un coàut a` chaque transformation potentielle du modèle. Typiquement la fonction d'énergie est une somme de deux termes, le premier rapproche le modèle déformé, des caractéristiques d'image, tandis que le deuxième pénalise les grandes déformations du modèle. La recherche sur des transformations est faite efficacement en

exploitant les propriétés de cette représentation pour les formes déformables. Cette approche donne une solution optimale globale au problème de correspondance qui permet de détecter des objets déformables sans aucune sorte d'occlusion et le désordre de fond.

FIG. 1.10 - polygones triangulaires d'un lapin et d'une poire.

1.5.5 Méthodes basées sur l'extraction de squelette

La représentation des formes en squelette est introduite par Blum [Bub 98]. Elle a la possibilitéde conserver sous forme compacte un grand nombre d'informations topologiques et géométriques de la forme initiale. Un autre avantage qu'il faut signaler est le fait que les squelettes ont une structure de graphe (voire figure 1.9) qui permet d'utiliser les puissants outils issus de la théorie des graphes. Le squelette d'un objet est une représentation de la forme dans une dimension inférieure. Pour un objet surfacique (2D), le squelette est un ensemble de lignes centrées dans la forme, par contre pour les objets 3D il existe deux types de squelettes. Les squelettes surfaciques qui sont un ensemble de surfaces centrées dans la forme et les squelettes curvilignes 3D qui sont un ensemble de lignes centrées dans la forme.

FIG. 1.11 - Squelettes topologiques de quelques objets.