Reconnaissance des objets polyédriques

3.3 Calcul de la carte de profondeur

3.3.1 Modèle géométrique de système de vision [Ait06]

3.3.1.1 Description du système

La figure 2.1 nous illustre un modèle géométrique d'un système de vision stéréoscopique non anthropomorphe (est un système dont les axes des caméras ne sont pas coplanaires), équipéde deux caméras en mouvement de rotation. Dont on a :

- IM1 (resp. IM2) est le plan de projection de la camra1 (resp. camra2), - L1, L2 : les lentilles des deux caméras (centres optiques),

- P1, P2 : points d'impact des axes optiques sur les plans IM1, IM2,

- (P1, U1, V1) : repère cartésien orthonormé-dit théorique- liéau plan IM1, construit ainsi :

- P1U1 est parallèle aux lignes de l'image IM1,

- P1U1 est parallèle aux colonnes de l'image IM1 (sur une caméra CCD¹ les lignes sont perpendiculaires aux colonnes [ABI89]),

- l'unité, que ce soit sur _O1U1 ou _O1V1 est soit le pixel ou le millimètre (mm). Le passage d'une unitéa` l'autre (pixel-mm par exemple) obéit a` la transformation suivante :

U1 = (ex).u1

'Charged Coupled Device

V1 = (ez).v1

Sachant que (ex, ez) représentent les facteurs de changements d'échelle et (U1, V1) (resp. (u1, v1)) Les coordonnées d'un point image dans le système o`u l'unitéest le pixel (resp. le mm)

- (P2 U2 V2) : repère cartésien orthonormé-dit théorique- lier au plan IM2, construit de manière analogue a` (P1 U1 V1),

- (O1 x1 y1 z1) [resp. (O2 x2 y2 z2)] : Repère cartésien orthonormé-dit théorique- liéa` la camra1 (resp la camra2) construit de la manière suivante :

- O1 (resp. O2) est situésur l'axe optique de la camra1 (resp. camra2) a` une distance d1 (resp. d2) de P1 (resp. P2). La valeur de d1) (resp. d2)) peut varier d'un mouvement a` un autre ; le centre de rotation de la caméra n'est pas connue et peut changer a` chaque rotation (voir figure)

- O1O1 ^(resp. _O2O2) est parallèle a` P1V1 (resp. P2V2),

- L'unitéutilisée sur ce repère est le mm,

- O1x1 et O2x2 sont colinéaires.

- è1 ( resp. è2 ) : angle de rotation de la camra1 (resp. camra2) autour de l'axe O1z1 (resp. O2z2),

- p : distance entre O1 _et O2,

- è2 : angle d'inclinaison de la camra2 par rapport a` la camra1 ;

- f : distance focale.

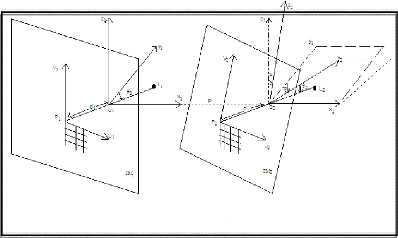
FIG. 3.2 - Modélisation géométrique de la tête de vision stéréoscopique.

3.3.2 Coordonnée projectifs avant et après rotation

Un point P(x,y,z) se projette sur le plan image en un point P1(U1); V1)) sur l'image1, et en un point P2(U2); V2)) sur image2, comme sera ^montrédans les fonctions suivantes :

· Avant rotation

(a) Sur IM1

U = (ex).f.		- cos(è1).x + sin(è1).y
		sin(è1).x + cos(è1).y + d1 - f
V = (ez).f.	-Z
	sin(è1).x + cos(è1).y + d1 - f

(b) Sur IM2

U2 = (ex).f.

- cos(è2).(x - p) + sin(è2).(y. cos(?) + z. sin(?)) sin(è2).(x - p) + cos(è2).(y. cos(?) + z. sin(?)) + d2 - f

sin(?).y - cos(?).z

V2 = (ez).f. sin(è2).(x - p) + cos(è2).(y. cos(?) + z. sin(?)) + d2 - f

Apres un certain nombre de rotation des caméras d'un angle (a1 ,a2 ) autour de _O1z1 (resp.O1z2 ) a` partir de sa position de départ a1 (resp. a2 ); Les cordonnées de projection du point objet P(x,y,z) sur les deux images IM1 et IM2 changent.

(a) i. Sur IM1

U = (ex).f.		- cos(è1 + a1).x + sin(è1 + a1).y
		sin(è1 + a1).x + cos(è1 + a1).y + d1 - f
V = (ez).f.	-Z
	sin(è1 + a1).x + cos(è1 + a1).y + d1 - f

ii. Sur IM2

cos(è2 + a2).(x - p) + sin(è2 + a2).(y. cos(?) + z. sin(?))

Uk 2 = (ex).f. sin(è2 + a2).(x - p) + cos(è2 + a2).(y. cos(?) + z. sin(?)) + d2 - f

3.3.3 Relations entre les cordonnes 2D et 3D

u1 = ex.f	- cos(è1).x + sin(è1).y
	sin(è1).x + cos(è1).y + d1 - f

-z

sin(è1).x + cos(è1).y + d1 - f

On note que x=X.(d1-f) ,y=Y.(d1-f) donc on aura

_v1 = ex. f

- cos(è1).X + sin(è1).Y

u1 = ex.f sin(è1).X + cos(è1).Y + 1 (1)

v1 = ex.f

-Z sin(è1).X + cos(è1).Y + 1 (2)

On divise (1) sur (2), on aura

.Y (3)

X

?

R

?

R?_..Z = cos(è1).X - sin(è1).Y cos(è1) sin(è1) Z = .

R

uk = ex . f 1

- cos(è1 + á).x + sin(è1 + á).y sin(è1 + á).x + cos(è1 + á).y + d1 - f

On a aussi

vi = ex._f

-z

sin(è + á1).x + cos(è1 + á).y + d1 - f On note que x=X.(d-f) ,y=Y.(d-f) donc on aura

uk = ex.f 1	- cos(è1 + á).X + sin(è1 + á).Y (4) sin(è1 + á).X + cos(è1 + á).Y + 1
v^k1= ex.f		-Z (5) sin(è1 + á1).X + cos(è1 + á).Y + 1

On remplace (3) dans (5)

vi = ez. f.	cos(è1) 1 .X + sin(è1) 1 .Y R0 R0
	sin(è1 + á1).X + cos(è1 + á).Y + d1 - f

Donc on a

X.(sin(è1 + á).v^k₁ + ez.f ^cos(è1) )+ Y.(v^k ₁. cos(è1 + á) - ez.f.^sin(è1) ) + v1 = 0

_R0 _R0

1 1

On remplace :

A = sin(è1 + á).v^k₁ + ez.f cos(è1)

R0 1

B = v^k₁. cos(è1 + á) - ez.f. sin(0è1)

1

C = v1

Donc on a A.X + B.Y + C = 0 X = On remplace x dans (4) on aura			-B.Y - C
			A
u^k1 = ex.f		- cos(è1 + á). A (-B.Y-9 + sin(è1).Y
		sin(è1).(^-B.X^-C) + cos(è1).Y + 1
sin(è1).(	-B.Y - C A ).u^k 1+u^k 1. cos(è1).Y +uk 1 = ex.f(- cos(è1+á).(					-B.Y - C A )+sin(è1).Y

1 +uk1 . sin(è1+á).C+ex.f. cos(è1+á).C

(-u^k )

Y = A

-ex. f.sin(è1+ á) + u^k₁. cos(è1 + á) . sin(è1+á).B-_Aex.f. cos(è1+á).B

3.3.4 Conclusion

Dans cette section on a présentécomment calculer la 3^eme coordonnée a` partir des coordonnées 2D par les différentes équations et leur démonstration . Après qu'on a trouvéla relation entre les coordonnées 2D et les coordonnées 3D, on remarque que, pour déterminer X, Y, Z il nous faut d'abord déterminer les angles de rotation á et è ; et pour cela nous allons exploiter le suivi d'un groupe de segments dans une séquence d'image.

3.4 Suivi d'un segment dans une s'equence d'images [ISR07]

Soit v0 = ai,0.u0 + bi, 0 l'equation d'un segment i dans une image o`u ai,0 est la pente du segment i dans l^'image0 et (u0, v0)les coordonnees 2D d'un point de segment de droite.

-a⁰ cos (á

ex^b f

D'apr`es certaines transformations on aura : ak. sm " = 0 =

(a) .

ä

Remarque :

Nous pouvons constater que l'expression des coordonnees images d'un point est de même forme dans les deux images (gauche et droite). C'est pourquoi, la relation entre les pentes des segments de droite dans les images successives droites va être de la même forme que celle obtenue par les segments des images gauches, donc il suffit de developper la relation sur les donnees de l'image IM1.

3.4.1 'Equation de mouvement d'un segment I :

,

Apr`es rotation d'un angle á : ai 1-ai,0 cos(á)sin(á) = bi,0

ex.f (6)

Apr`es rotation d'un angle â : ai,1-ai,0 cos(â)

sin(â) = bi,0

ex.f (7)

3.4.1.1 Application de la m'ethode

A partir du rapport entre les deux equation (6) et (7) on peut deduire que :

ai,1-ai,0 cos(á) ai,2-ai,0 cos(â) =

sin á sin â

Si on applique le même principe pour le segment j on obtient : aj,1-aj,0 cos(á) aj,2-aj,0 cos(â) =

sin á
sin â

ai,1-ai,0 cos(á) cos(á)

A partir de cette derni`ere equation on aura

cos(â) aj,2-aj,0 cos(â)

(aj,1.ai,0-ai,1.aj,0. cos(â))+(ai,2.aj,0-aj,2.ai,0. cos(á)+(aj,1.ai,2-ai,1.aj,2) =

0 si on remplace

c1 = aj,1.ai,0 - ai,1.aj,0

c2 = ai,2.aj,0 - aj,2.ai,0

c3 = aj,1.ai,2 - ai,1.aj,2

On aura :

c1 cos(â) + c2 cos(á) + c3 = 0 (A)

C'est une equation a` 2 inconnus, pour resoudre cette equation il faut une autre equation a` 2 inconnus, pour cela il suffit de prendre 2 autres segments

k et l, on aura : c_p,1 cos(â) + _cp,2 cos(á) = cp,3 (B)

Tel que :

cp,1 = al,1.ak,0 -- ak,1.al,0

cp,2 = ak,2.al,0 -- al,2.ak,0

cp,3 = al,1.ak,2 -- ak,1.al,2

La resolution de ce système d'equations (A) et (B) :

{

c1. cos(â) + c2. cos(á) = c3 cp,1. cos(â) + _cp,2. cos(á) = cp,3 Si det(c1 * cp,2 -- c2 * cp,1) =6 0

Alors :

cos(á) = ((c3*cp,2)-(cp,3*c2))

det

cos(â) = ((c1*cp,3)-(c3*cp,1))

det

La resolution de ce système necessite 4 segments dans 3 sequences d'images. La valeur de la solution est le mouvement effectuepar la camera pour l'obtention de l'image suivante donc une valeur qui reste constante si les segments consideres correspondent aux bons appariements. Nous pouvons enoncer la proposition suivante :

proposition :Soient i, j, k, l quatre segments de IM0, de IM1 i1, j1, k1l1 et i2,j2, k2, l2 de IM2 Les valeurs cos(á)et cos(â)obtenues après resolution du système correspondent aux mouvement reel de la camera si et seulement si chaque triplet de segments (i, i1, _i2),(j, j1, j2), (k, k1, k2),(l, l1, l2) contient le même segment dans les differentes images. La solution ayant engendrele plus grand score en nombre de quadruples de segments obtenus, sera la bonne

solution. Ainsi nous pouvons dire que nous avons résolu deux problèmes : le problème d'appariement et celui du mouvement des caméras.

3.4.1.2 Algorithme De Suivi :

Début

Extraction de contour de chaque image (IM1; IM2; IM3) Segmente les images (IM1; IM2; IM3)

Extraction de primitives (segments de droite) de IM1; Calculer la pente de chaque segment de IM1

Extraction de primitives (segments de droite) de IM2; Calculer la pente de chaque segment de IM2;

Extraction de primitives (segments de droite) de IM3; Calculer la pente de chaque segment de IM3;

Regrouper en groupe de quatre les segments de IM1 dans T1; Regrouper en groupe de quatre les segments de IM2 dans T2; Regrouper en groupe de quatre les segments de IM3 dans T3; - Pour tout groupe de segments de IM1 faire

- Pour tout groupe de segments de IM2 faire

- Pour tout groupe de segments de IM3 faire

- Calculer (cos a, cos â)

- Fin pour

- Fin pour

- Fin pour

Calculer le score pour chaque solution trouvée;

Choisir les groupes de segments qui engendrent le plus grand score;

Etablir la correspondance entre les segments de droite dans les différentes images ayant engendrés le plus grand score.

Fin.

Remarque :

- Les valeurs de cos(a)et cos(â)correspondent au mouvement effectuépar la caméra.

- - La bonne solution de cos(a) et cos(â) correspond a` la valeur ayant engendrée le plus grand score.

Conclusion (Méthode ) :

l'avantage de cette méthode est qu'elle permet de résoudre le problème d'estimation du mouvement.

On remplace cos(á) ou cos(/3)dans les formules précédentes, on aura les coordonnées 3D (X, Y, Z) de chaque point de l'image.