
Chapitre3
La conception et resultat d'expérimentation
3.1 Introduction
L'extraction de l'information concernant la structure des
formes presentées dans une image est un problème très
délicat dans le domaine de la vision par ordinateur. Bien qu'il ait
étéétudiédepuis longtemps, il n'y a pas de
méthode qui soit en même temps robuste, rapide et
générale.
3.2 La reconnaissance des objets
polyédrique
3.2.1 Choix des primitives
· Les segments 3d fournissent une représentation
simplifiée pour la scène.
· Un objet polyédrique est un ensemble de segments
3D.
· Les segments facilitent la détection des
jonctions.
La méthode de la reconnaissance qu'on a
développésuit les étapes représentées par
l'organigramme suivant :
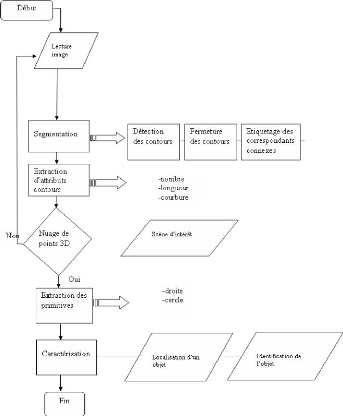
FIG. 3.1 - Organigramme de la méthode de reconnaissance
automatique des objets.
3.2.2 L'algorithme développépour la reconnaissance
des objets polyédrique
3.2.3 algorithme pour la localisation
1. Prendre une séquence d'images
2. 'Etablire un appariement (Suivi de segment de droite).
3. Déterminer le mouvement
4. D'eterminer les coordonn'ees X, Y, Z.
5. Reconstruction carte de profondeur(Reconstruction
projective).
6. D'eterminer :
(a) Les segments 3D.
(b) D'eterminer les jonctions
(c) Calculer les angles
(d) Reconnaàýtre la forme pr'esente dans la
scène
· D'eterminer les jonctions
3.2.3.1 Estimation des primitives
(a) Intersection segment / segment Soient 2 segments 3D [A1A2]
et [B1B2].
Trouver l'intersection I de ces 2 segments en fonction de
A1,A2,B1,B2.
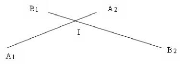
Solution :
Toujours sous forme param'etrique :
I est sur [B1B2] il s'exprime donc en param'etrique par
I = B + tB (B2 - B1)
I est aussi sur [A1A2] donc : I = A + tA (A2 - A1) Notez que
le paramètre t est diff'erent sur chaque segment. Dans le cas g'en'eral,
tA tB . On pose les vecteurs
VA = A2 - A1 et VB = B2 - B1
En remplaçant ceci dans les 2 'equations pr'ec'edentes, on
obtient : I = A + tA VB = B +tA VB
On a donc une 'equation a` 2 inconnues tA et tB . En projetant
cette 'equation sur l'axe X et sur l'axe Y,et sur Z on obtient un
système lin'eaires de 3 'equations a` 2 inconnues :
A1.x + tAVA.x = B1.x + tBVB.x A1.y + tAVA.y = B1.y
+ tBVB.y A1.z + tAVA.z = B1.z + tBVB.z
Soit :
tAVA.x - tBVB.x = B1.x - A.x tAVA.y - tBVB.y =
B1.y - A.y tAVA.z - tBVB.z = B1.z - A.z
Ou sous forme matricielle, en posant le vecteur T = tA,tB,0
le vecteur R = B -A Et la matrice 3x3
M= ~~~~~~~~
~~~~~~~~
VA.x VB.x 0
VA.y VB.y 0
VA.z VB.z 1
On obtient le système lineaire matriciel suivant :
MT = R
Si le determinant 3x3 de M est non nul, l'equation a une unique
solution qui se trouve en inversant la matrice M, l'inverse de M etant
noteM-1 On a :
T = M-1R
Remarque : seule la connaissance d'une des 2 valeurs TA ou TB
nous suffit pour trouver l'intersection I.
En notant ' det ' le determinant de 2 vecteurs 3D. Nous obtenons
donc pour tA par exemple :
tA = det((B - A),vB)/det(vA,vB)
(b) Calculer les angles on peut utiliser le produit scalaire. En
utilisant les definitions suivantes :
AB : vecteur de A a` B
- AC : vecteur de A a` C
|| : norme des vecteur (longueur (positif))
BAC : angle entre le sommet A et les points B et C
- Le produit scalaire . S'écrit de la manière
suivante :
AB . AC = |AB|×|AC|×cos (BAC)
Et donc on peux récupérer l'angle
Angle = arccos ( prodscalaire(AB,AC) /norme( AB) . norme(AC))
- Reconnaàýtre la forme présente dans la
scène
On regroupe les segments en quatre, pour chaque jonction on
calcule
l'angle Si les angles sont équivaux est prés de
90°on détecte un polyèdre
Conclusion
IL faudra d'abord calculer la carte de profondeur, pour cela on
va utiliser l'algorithme de développement de la section suivante [NAB
09]
| 


