CHAPITRE QUATRIEME
ESSAIE D'ELABORATION D'UN PLAN DE
PRODUCTION
Le complexe Théicole de Butuhe est une entreprise agro
industrielle qui produit et commercialise le thé sec dans l'objectif du
lucre. Ainsi, cette entreprise cherche à maximiser ses profits et
minimiser ses coûts. Cette entreprise qui se trouve en situation de sous
activité doit faire tout son possible afin que le niveau de stockage
soit suffisant à chaque période de manière à faire
face aux alternatives de la demande. Ceci signifie que pour faire face à
cette situation de sous activité, le CTB doit rendre régulier son
cycle d'exploitation, ce qui implique pourtant une hausse de coût de
production.
Le CTB SPRL pourra réaliser ses objectifs de production
en rendant minimum la fonction économique qui représente son
coût de production mensuel. Pour y arriver, elle devra influencer la
variation du prix d'achat des feuilles vertes et la rémunération
des facteurs de production suivant les fluctuations des prix du marché.
Dans cette partie de notre travail, nous essayerons de déterminer la
quantité optimale à produire pour que le coût de production
soit minimum.
Cependant, le programme que nous élaborerons et que
nous recommanderons au CTB SPRL n'est réalisable que si tous les moyens
sont réunis. L'analyse du dernier bilan nous a fait voir les
capacités actuellement installées au sein du CTB SPRL. Il en est
sorti une situation de sous activité et le volume de la zone de risque
par des fonds propres c'est-à-dire les apports nouveaux ou les fonds
empruntés à long ou moyen terme pour relancer la production en
vue de donner un ballon d'oxygène à l'entreprise.
En vue de rendre régulière la production, nous
avons formulé un programme linéaire de production. Nous avons
énoncé les problèmes d'usinage de thé en vue d'en
constater les contraintes.
Pour obtenir le thé sec noir, les ouvriers lui font
subir les opérations de flétrissage, roulage, fermentation,
séchage et triage. Le thé sec produit par le CTB SPRL est
destiné, en majeure partie à l'exportation.
L'activité normale de l'usine du CTB SPRL est de 24
heures par jour. Mais la capacité actuellement installée permet
d'exploiter les machines à 55%. Il se dégage donc une
dégradation de la production jusqu'à une réalisation
annuelle de 412,5 tonnes de thé sec pour un travail machine
réalisé journellement pendant 13h20'. L'activité d'usinage
est de 23 445 minutes et celle de triage est de 855 minutes
mensuellement.
Notons toutefois que, les travaux d'usinage s'effectuent
à la chaîne jusqu'à l'obtention du thé brut. Le
triage quant à lui différencie les grades sur base desquels l'on
détermine les qualités à exporter et celles à
vendre localement. L'usinage de 100 kg de thé brut prend 7 minutes et
triage de chaque 2 tonnes prend 60 minutes soit une proportion de 3 minutes
pour le thé local et 27 minutes pour le thé Export en vue de les
distinguer dans 100 kg trillés.
L'opération de flétrissage des feuilles vertes
s'effectue sur 6 paires de bacs chacun a une capacité d'accueil de 100
kg de feuilles vertes destinées à l'usinage et peut permettre 13
approvisionnement par mois. Le taux d'extraction est évalué
à 22,2% c'est-à-dire que 4,5 kg de feuilles vertes usinées
produit 1 kg de thé sec brut. Ces deux alternatives nous permettent
d'estimer à 34375 kg de thé que le CTB SPRL peut produire et
vendre par mois sachant que l'on ne peut exporter moins de 15 tonnes.
Les prix de vente de thé sont réglementés
et fixés par la mercuriale. Celle-ci présente des prix
relativement bas ne pouvant permettre la réalisation des
bénéfices énormes. Ce qui fait que le CTB détermine
son coût de revient unitaire en fonction du prix de vente. Pour notre
analyse, il se révèle que les coûts unitaires issus de
l'exploitation sont supérieurs et ne permettent pas la
réalisation d'un bénéfice surtout que les prix de vente
imposés à l'entreprise sont inférieurs. La situation de
marasme que connaît cette entreprise nous impose leur usage dans
l'étude d'un planning optimal de production. Ces coûts unitaires
sont de 1,5 USD et 1,67 USD respectivement pour le thé local et le
thé à l'exportation.
Si Z représente le coût total de production,
X1 la quantité de thé à vendre localement et
X2 la quantité de thé à exporter, nous
formulons le programme linéaire suivant :
Min [Z=1,5X1 + 1,672X2]
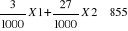
S/C X1 + X2 = 34375
X2 = 15000
X1 = 0; X2 = 0
Pour trouver la solution optimale, nous appliquons
l'algorithme de DANTZING. Ce dernier nous permettra de déterminer les
quantités optimales de X1 ET X2 pour que le
coût de production soit minimum.
Pour éliminer les inégalités,
introduisons les variables d'écarts :
Min [Z=1,5X1 + 1,672X2 +
0t1+0t2+0t3]

S/C X1 + X2 - t2 =
34375
X2 - t3 = 15000
X1 = 0; X2 = 0; t1= ;
t2= ; t3=0
Mais comme t1, t2, t3 sont
négatifs, nous introduisons les variables artificielles afin de
déterminer les bases admissibles (M ? 8) :
Min [Z=1,5X1+1,672X2+
0t1+0t2+0t3+MV1+MV2+MV3]
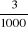
X1 +

X2 - t1 + V1 = 855
S/C X1 + X2 - t2 +
V2 = 34375
X2 - t3 + V3 =
15000
X1 = 0; X2 = 0; t1= ;
t2= ; t3=0 ; V1=0 ;
V2=0 ; V3=0
Ainsi, nous déterminerons les bases
admissibles :
Si X1=X2=0 et
t1=t2=t3=0
Alors on déduit que
V1 = 855
V2 = 34375
V3 = 15000
Et comme ces valeurs sont positives, nous admettons que les
bases sont PV1, PV2, PV3. Nous pouvons alors
amorcer la construction du tableau de simplexe.
Tableau XXIV: Tableau de Simplexe
|
Cj
|
Base
|
Cj
|
1,55
|
1,672
|
0
|
0
|
0
|
M
|
M
|
M
|
|
|
CONCLUSION
|
|
Po
|
P1
|
P2
|
Pt1
|
Pt2
|
Pt3
|
PV1
|
PV2
|
PV3
|
|
M
M
M
|
PV1
PV2
PV3
|
855
34375
15000
|
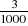
1
0
|

1
1
|
-1
0
0
|
0
-1
0
|
0
0
-1
|
1
0
0
|
0
1
0
|
0
0
1
|
31667
34375
15000 min
|
-0,027
-1
1
|
P2 entre, k = 2
PV3 sort, r = 3
|
|
Zj - Cj
|
50230M
|
|
|
-M
|
-M
|
-M
|
0
|
0
|
0
|
|
|
Pivot = 1
|
|
M
M
1,672
|
PV1
PV2
P2
|
450
19375
15000
|
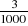
1
0
|
0
0
1
|
-1
0
0
|
0
-1
0
|

1
-1
|
1
0
0
|
0
1
0
|
|
16667 min
19375
-
|
37,037
-37,037
37,037
|
Pt3 entre, k = 5
PV1 sort, r = 1
|
|
Zj - Cj
|
19825M +25080
|
|
0
|
-M
|
-M
|
|
0
|
0
|
|
|
|
Pivot = 0,027
|
|
0
M
1,672
|
Pt3
PV2
P2
|
16666,67
2708,33
31666,67
|
0,111
0,889
0,111
|
0
0
1
|
-37,037
37,037
-37,037
|
0
-1
0
|
1
0
0
|
|
0
1
0
|
|
-
100308 min
-
|
1
0,027
1
|
Pt1 entre, k = 3
PV2 sort, r = 2
|
|
Zj - Cj
|
2708,33M +52946,67
|
0,889M -1,314
|
0
|
37,037M -61,926
|
-M
|
0
|
|
0
|
|
|
|
Pivot = 37,037
|
|
0
0
1,672
|
Pt3
Pt1
P2
|
19375
73,125
34375
|
1
0,024
1
|
0
0
1
|
0
1
0
|
-1
-
-1
|
1
0
0
|
|
|
|
19375
1,755 min
34375
|
-41,67
41,67
-41,67
|
P1 entre, k = 1
Pt1 sort, r = 2
|
|
Zj - Cj
|
57475
|
0,172
|
0
|
0
|
-1,672
|
0
|
|
|
|
|
|
Pivot = 0,024
|
|
0
1,5
1,672
|
Pt3
P1
P2
|
16328,125
3046,875
31328,125
|
0
1
0
|
0
0
1
|
-41,67
41,67
-41,67
|
0,125
-1,125
0,125
|
1
0
0
|
|
|
|
|
|
|
|
Zj - Cj
|
56950,9375
|
0
|
0
|
-1,167
|
-1,4785
|
0
|
|
|
|
|
|
|
Comme il n'existe plus de Zj-Cj >0 et
que l'on ne sait plus entrer les vecteurs dans la base, nous concluons avoir
obtenue la solution optimale. Les quantités à produire sont
respectivement 3046,875 kg de thé à vendre localement 31828,125
de thé à exporter et le coût maximal est de 56950,9375 $US.
Il se dégage un excédent de 16328,125 kg sur le minimum du
thé à exporter et la saturation des installations de triage et
d'usinage.
|
|



