SECTION III : ANALYSE DE LA DEMANDE POTENTIELLE DU
THE
En marketing, il faut vendre avant de produire pour ainsi dire
qu'il vaut mieux produire ce dont on est capable de vendre. Cela demande de
s'imprégner avant tout de la situation de marché avant
d'élaborer tout plan de production. Ce qui nous amène à
analyser la demande potentielle sur base de laquelle nous allons
déterminer les quantités à produire. L'étude
corrélative des ventes et de la production ainsi que l'analyse
régressive des ventes par rapport à la production nous
permettront d'établir leur liaison causale. Nous essayerons aussi
d'élaborer les prévisions de production qui répondent aux
alternatives de la demande potentielle.
En analysant la demande, nous devons tenir compte du niveau de
stockage c'est-à-dire la production de la période et le stock
initial sur base duquel l'entreprise pourra faire face aux diverses
alternatives de la demande.
III.1. PRESENTATION DES DONNEES
Tableau XI : Situation production du CTB
SPRL de 2003 à 2008
|
Annnée
|
Mois
|
Stock
initial
|
Production
|
Vente
|
Rebus, vol, don &
échantillonnage
|
STOCK FINAL
|
|
2003
|
Janvier
|
6872,5
|
30346
|
37218,5
|
0
|
0
|
|
Février
|
0
|
30204
|
25567
|
0
|
4637
|
|
Mars
|
4637
|
43306
|
44900
|
22,5
|
3020,5
|
|
Avril
|
3020,5
|
22085
|
16701,5
|
1976,5
|
6427,5
|
|
Mais
|
6427,5
|
35938,5
|
32855,2
|
2319
|
7191,8
|
|
Juin
|
7191,8
|
34811
|
31560
|
42,
|
10400
|
|
Juillet
|
10400
|
16900
|
7968,5
|
831,5
|
193000
|
|
aoûte
|
19300
|
6697,2
|
12837,2
|
0
|
13160
|
|
Septembre
|
13160
|
2312,5
|
0
|
22,5
|
15450
|
|
Octobre
|
15450
|
17231
|
028642
|
19
|
4020
|
|
Novembre
|
4020
|
13744
|
5504
|
0
|
12260
|
|
Décembre
|
12260
|
4708,2
|
16968,2
|
0
|
0
|
|
2004
|
Janvier
|
0
|
17699
|
0
|
9
|
17690
|
|
Février
|
17690
|
15529
|
23229
|
20
|
9970
|
|
Mars
|
9970
|
0
|
2728
|
0
|
7242
|
|
Avril
|
7242
|
22085
|
25088
|
18
|
4221
|
|
Mais
|
4221
|
14647
|
0
|
0
|
18868
|
|
Juin
|
18868
|
10403
|
28960
|
145
|
166
|
|
Juillet
|
166
|
6942
|
3020
|
20,5
|
4067,5
|
|
aoûte
|
4067,5
|
2874
|
0
|
0
|
6941,5
|
|
Septembre
|
6941,5
|
7723
|
370
|
0
|
14294,5
|
|
Octobre
|
14294,5
|
18354
|
29748,2
|
178,3
|
2722
|
|
Novembre
|
2722
|
11345
|
0
|
1807
|
12260
|
|
Décembre
|
12260
|
20925,9
|
13703,4
|
12,5
|
19470
|
|
2005
|
Janvier
|
19470
|
31782
|
17410
|
402
|
33440
|
|
Février
|
33440
|
35962
|
33184,1
|
39,5
|
36178,4
|
|
Mars
|
36178,4
|
32801
|
32822
|
12,3
|
36145,1
|
|
Avril
|
36145,1
|
19887
|
27620
|
26
|
28386,1
|
|
Mais
|
28386,1
|
14710
|
33176,8
|
8266,3
|
1653
|
|
Juin
|
1653
|
2100
|
0
|
0
|
3753
|
|
Juillet
|
3753
|
3110
|
3786
|
23,3
|
3035,7
|
|
Aoûte
|
3053,7
|
875
|
3073
|
83,7
|
772
|
|
Septembre
|
772
|
0
|
0
|
2
|
770ss
|
|
Octobre
|
770
|
2700
|
0
|
0
|
3470
|
|
Novembre
|
3470
|
0
|
2410
|
0
|
1060
|
|
Décembre
|
1060
|
5115
|
1420,5
|
12,5
|
4742
|
|
2006
|
Janvier
|
4742
|
22436
|
3520
|
109
|
23549
|
|
Février
|
23549
|
7215
|
25556
|
84
|
5124
|
|
Mars
|
5124
|
9943,6
|
4673
|
40,6
|
10354
|
|
Avril
|
10354
|
9982
|
16821
|
0
|
3515
|
|
Mai
|
3515
|
8205
|
4340
|
36,8
|
7343,2
|
|
Juin
|
7343,2
|
0
|
0
|
0
|
7343,2
|
|
Juillet
|
7343,2
|
0
|
3434,2
|
0
|
3909
|
|
Août
|
3909
|
01740
|
3900
|
9
|
0
|
|
Septembre
|
0
|
8108
|
0
|
4,2
|
1735,8
|
|
Octobre
|
1735,8
|
6484
|
5920
|
30,8
|
3893
|
|
Novembre
|
3893
|
7588
|
1716
|
0
|
8661
|
|
Décembre
|
8661
|
0
|
2730
|
484
|
13035
|
|
2007
|
Janvier
|
13035
|
0
|
0
|
0
|
13035
|
|
Février
|
13035
|
0
|
0
|
0
|
13035
|
|
Mars
|
13035
|
0
|
13035
|
0
|
0
|
|
Avril
|
0
|
0
|
0
|
0
|
0
|
|
Mai
|
0
|
0
|
0
|
0
|
0
|
|
Juin
|
0
|
0
|
0
|
0
|
0
|
|
Juillet
|
0
|
0
|
0
|
0
|
0
|
|
Août
|
0
|
0
|
0
|
0
|
0
|
|
Septembre
|
0
|
0
|
0
|
0
|
0
|
|
Octobre
|
0
|
0
|
0
|
0
|
0
|
|
Novembre
|
0
|
0
|
0
|
0
|
0
|
|
Décembre
|
0
|
0
|
0
|
0
|
0
|
|
2008
|
Janvier
|
0
|
0
|
0
|
0
|
0
|
|
Février
|
0
|
15284
|
5280
|
110
|
9894
|
|
Mars
|
9894
|
14222
|
120
|
103
|
23893
|
|
Avril
|
23893
|
9004
|
24970
|
27
|
7900
|
|
Mai
|
7900
|
24710
|
24030
|
195
|
8385
|
|
Juin
|
8385
|
6857
|
220
|
12
|
15010
|
|
Juillet
|
15010
|
0
|
15010
|
0
|
0
|
|
Août
|
0
|
441
|
0
|
4
|
437
|
|
Septembre
|
437
|
14050
|
420
|
152
|
13915
|
|
Octobre
|
13915
|
1750
|
15225
|
35
|
405
|
|
Novembre
|
405
|
0
|
0
|
20
|
385
|
|
Décembre
|
385
|
0
|
225
|
80
|
80
|
Source : service commercial du C.T.B
SPRL
De ce tableau on constate que l'on produit sans
tenir compte de la situation de stockage. Ce qui fait qu'on peut constater des
stocks relativement lourds. Ce stockage engage des charges
supplémentaires à l'entreprise et partant, diminuent le
résultat. L'entreprise peut des charges supplémentaires a
l'entreprise et partant, diminuent le résultat,l'entreprise peut
éviter ces charges en mettant en place un programme de production c'est
-à- dire celui qui répond aux demandes de la clientèle.
III.2. ANALYSE TENDANCIELLE DES VENTES
Il est maintenant impérieux que nous analysions la
demande de thé du C.T.B SPRL. Nous estimons que les l'étude
même des vente qui nous est utile pour ce fait. Il est en effet reconnu
que les statiques économiques fournissent des mesures quantitatives des
phénomènes économiques dans le secteur public et
privé de l'économie. La statistique nous permet de mener une
analyse des données, d'en faire une interprétation et la
projection des tendances futures. Nous en faisons un cas dans cette partie de
notre travail.
Les données en notre possession sont observées
à intervalle de temps réguliers : le moins. Ce qui nous
amène à une analyse des séries chronologiques. Celles - ci
appelées encore chronique se rapportent pour la majeur partie aux
phénomènes économiques mais aussi à leur
complexité. Les chroniques sont en effet caractérisées par
des composantes qui sont de quatre ordres :
Ø La tendance générale ou trend ;
Ø Les variations saisonnières ;
Ø Les variations cycliques ;
Ø Les variations irrégulières.
D'où pour inférer les tendances dans le futur,
il faut au préalable dégager de l'ensemble des observations la
tendance générale et les éléments influents.
III.2.1. ANALYSE STATISTIQUE DE LA DEMANDE DE THE
L'analyse de la demande de thé nous amène
à déterminer un modèle approprié que nous nous
proposons d'utiliser dans la détermination des prévisions des
ventes en fonction desquelles nous déterminerons les quantités
à produire. En effet, la recherche d'un planning optimal de produit est
sujette à ces fluctuations de la demande.
Il importe alors de fixer la façon dont les composantes
de la chronique se superposent pour former les données brutes. Si nous
admettons que Yt est la valeur observée de série
chronologique, Ct la valeur de la composante cyclique, St celle de la valeur
saisonnières composante irrégulière et Tt la valeur de la
tendance générale, il s'observe que Yt est de ces quatre
dernières composantes.
Yt = f ( Tt, St, It)
Le choix d'un modèle revient alors à
spécifier la fonction f. Il ressortira que :
- le modèle est additif (Yt = Tt + Ct+St + It) si et
seulement si les composantes St, Ct et It sont indépendantes de
Tt ;
- le modèle est multiplicatif
(Yt=Tt x Ct x St x It)
si et seulement si les composantes St, Ct et
It sont proportionnels à Tt.
Nous utilisons la méthode de la droite de
régression des écarts- type annuels de différentes
années en fonction de leurs moyennes respectives pour choisir l'un de
ces modèles. S'il ressort que dans la représentation graphique de
l'équation régressive, la droite trouvée soit
parallèle à l'axe des abscisses, alors on a faire à un
modèle additif. S'il ressort par contre que la droite trouvée ait
une tendance croissante ou décroissante, on a à faire à un
modèle multiplicatif.
Il faut alors calculer pour chaque année :
- la moyenne arithmétique :  avec i = 1, 2, ..., n (années) avec i = 1, 2, ..., n (années)
- l'écart-type :  et j = 1, 2, ..., p (mois) et j = 1, 2, ..., p (mois)
Et calculer enfin la régression de ä en y et en
étudier la pente représenter par a.
Tableau XII : calcul de
l'équation de régression
|
ANNEE
|
Moyenne
arithmétique
|
(yi) 2
|
Ecart type
|
(yi)(äi)
|
|
2003
2004
2005
2006
2007
2008
|
21726,84167
10570,55250
12908,53750
6050 ,85000
1086,2500
7125,00000
|
47205,5649x104
11173,65802x104
16663,03404 x104
3661,27857 x104
117,993906 x104
5076,5625 x104
|
1,3265045 x104
1,209778 x104
1,407475 x104
0,7200766 x104
0,3602683 x104
0,947375 x104
|
28820,75308 x104
12788,02235 x104
18168,44367 x104
4357,07546 x104
391,34151 x104
6750,046816 x104
|
|
SOMME
|
59467,99417
|
83897,99511 x104
|
5,9714774 x104
|
71275,68289 x104
|
Source : Nous- même à
l'aide du tableau XI

 

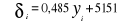
Mais il nous faut tester la signification du coefficient
angulaire pour nous assurer de la justesse de la régression de ä en
y. Nous utilisons de ce fait le test de student au seuil de 5% afin de savoir
si a est significativement différent de zéro.
Le rapport critique s'établit par t = 
Avec S =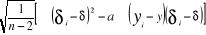
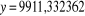 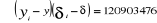
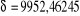 
S = 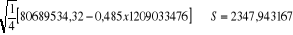
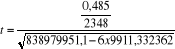 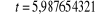

La table de student donne au seuil de 5% une valeur
théorique 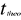 = 2, 776. = 2, 776.
Comme nous constatation que t* = 5,98765 supérieur
à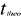 = 2,776, nous concluons à 95% que a est significativement
différent de zéro et est compris entre les valeurs
décrites par l'intervalle ci-après : = 2,776, nous concluons à 95% que a est significativement
différent de zéro et est compris entre les valeurs
décrites par l'intervalle ci-après :
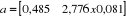

Graphique 1 : représentation
graphique de la droite de régression
 
5151
0

En observant ce graphique, nous remarquons une tendance
croissante avec une pente positive supérieure à 0,10. Nous
pouvons alors conclure qu'il faut adopter la méthode multiplicative
(Yt = T x S x C x I). Ceci présuppose la
présence dans la chronique de la tendance générale
Tt et des éléments influents. Nous nous
efforçons de déterminer ces composantes dans les point suivant
afin de d'établir des prévisions proprement dites.
1°) Détermination de la tendance
générale
L'examen préalable de nos données montre une
présence exagérée des vides. Ce qui fait qu'au lieu
d'avoir12 observations annuelles, l'on peut compte facilement 11 pour
l'année 2003 ; 8 pour l'année 2004 ; 9 pour
l'année 2005 ; ces vides peuvent s'expliquer par des
irrégularités dans la production. Ce qui fait que l'entreprise se
trouve dans l'impossibilité de satisfaire sa clientèle. Il vaut
mieux rendre régulier le cycle d'exploitation. Mais pour nous permettre
toute analyse afin de déterminer la tendance des ventes, nous appliquons
la méthode des moyennes mobiles sur 12 mois.
En effet, si nous voulons prévoir les ventes, nous
devons fixer d'avance la tendance historique tout en tenant compte des
contraintes internes et externes de l'entreprise et de sa politique
générale. La prévision des ventes doit donc comporter un
double aspect c'est-à-dire volontariste et décisionnel.
D'où, nous privilégions le court terme c'est-à-dire
l'application de la méthode des moyennes mobiles. Cette dernière
est l'évolution d'un phénomène en fonction du temps
à court terme après élimination des circonstances
accidentelles.
L'application de la méthode des moyennes mobiles
consiste à remplacer chaque terme de la série par une moyenne
arithmétique simple ou pondérée. La moyenne mobile est
déterminée par l'expression :

Mij = la moyenne mobile correspondant à
l'année i et au mois j
Yij = la valeur observée de l'année i
et au mois j
Les moyennes mobiles sont donc centrées sur 12 mois
utilisés dans leurs calculs. La première moyenne mobile sera
alors placée en face du 7ème mois qui est une moyenne
mobile basée sur 12 valeurs mensuelles de la première
année ; la deuxième sera placée en face du mois
d'Août qui correspond au septième mois de la nouvelle série
c'est-à-dire de février de la première année
à Janvier de la deuxième.
Tableau XIII : calcul des moyennes
mobiles
|
ANNEES
|
MOIS
|
VENTES Yij
|
Moyennes mobiles Mij
|
Rapport en %
Yij/Mij
|
|
2003
|
Janvier
|
37218,5
|
-
|
-
|
|
Février
|
25567
|
|
|
|
Mars
|
44900
|
|
|
|
Avril
|
16701,5
|
|
|
|
Mais
|
32855,2
|
|
|
|
Juin
|
31560
|
|
|
|
Juillet
|
7968,5
|
20176,07
|
39,49
|
|
Aoûte
|
12837,2
|
18527,88
|
69,29
|
|
Septembre
|
0
|
16673,30
|
0,00
|
|
Octobre
|
28642
|
15265,57
|
187,62
|
|
Novembre
|
5504
|
14246,04
|
38,64
|
|
Décembre
|
16968,2
|
12768,74
|
132,89
|
|
2004
|
janvier
|
0
|
12454,22
|
0,0
|
|
Février
|
23229
|
11713,15
|
198,32
|
|
Mars
|
2728
|
11193,63
|
24,37
|
|
Avril
|
25088
|
11255,19
|
222,90
|
|
Mais
|
0
|
11071,95
|
0,00
|
|
Juin
|
28960
|
10706,58
|
270,49
|
|
Juillet
|
3020
|
11295,97
|
26,74
|
|
Aoûte
|
0
|
12436,18
|
0,00
|
|
Septembre
|
370
|
14104,89
|
2,62
|
|
Octobre
|
29748,2
|
15464,31
|
192,37
|
|
Novembre
|
0
|
16952,18
|
0,00
|
|
Décembre
|
13703,4
|
17127,88
|
80,01
|
|
2005
2006
|
janvier
|
17410
|
15953,13
|
109,13
|
|
Février
|
33184,1
|
16113,08
|
205,95
|
|
Mars
|
32822
|
16225,71
|
202,28
|
|
Avril
|
27620
|
14970,78
|
184,49
|
|
Mais
|
33176,8
|
13831,69
|
239,86
|
|
Juin
|
0
|
13420,32
|
0,00
|
|
Juillet
|
3786
|
12329,78
|
30,71
|
|
Août
|
3073
|
11433,20
|
26,88
|
|
Septembre
|
0
|
9942,48
|
0,00
|
|
Octobre
|
0
|
8319,65
|
0,00
|
|
Novembre
|
2410
|
6668,16
|
36,14
|
|
Décembre
|
1420,5
|
5466,63
|
25,98
|
|
Janvier
|
3520
|
5451,97
|
64,56
|
|
Février
|
25556
|
5471,77
|
467,05
|
|
Mars
|
4673
|
5506,23
|
84,87
|
|
Avril
|
16821
|
5752,89
|
292,39
|
|
Mais
|
4340
|
5970,64
|
72,69
|
|
Juin
|
0
|
5996,29
|
0,00
|
|
Juillet
|
3434,2
|
5904,18
|
58,17
|
|
Aoûte
|
3900
|
4692,68
|
83,11
|
|
Septembre
|
0
|
3976,27
|
0,00
|
|
Octobre
|
5920
|
3623,81
|
163,36
|
|
Novembre
|
1716
|
2742,10
|
62,58
|
|
Décembre
|
2730
|
2561,27
|
106,59
|
|
2007
|
janvier
|
0
|
2418,18
|
0,00
|
|
Février
|
0
|
2112,58
|
0,00
|
|
Mars
|
13035
|
1950,08
|
668,43
|
|
Avril
|
0
|
1703,42
|
0,00
|
|
Mais
|
0
|
1385,25
|
0,00
|
|
Juin
|
0
|
1200,00
|
0,00
|
|
Juillet
|
0
|
1086,25
|
0,00
|
|
Aoûte
|
0
|
1306,25
|
0,00
|
|
Septembre
|
0
|
988,13
|
0,00
|
|
Octobre
|
0
|
1490,42
|
0,00
|
|
Novembre
|
0
|
3532,08
|
0,00
|
|
Décembre
|
0
|
4542,50
|
0,00
|
|
2008
|
janvier
|
0
|
5177,08
|
0,00
|
|
Février
|
5280
|
5802,50
|
91,00
|
|
Mars
|
120
|
5820,00
|
2,06
|
|
Avril
|
240970
|
6471,88
|
385,82
|
|
Mais
|
24030
|
7106,25
|
338,15
|
|
Juin
|
220
|
7115,63
|
3,09
|
|
Juillet
|
15010
|
|
|
|
Aoûte
|
0
|
|
|
|
Septembre
|
420
|
|
|
|
Octobre
|
15225
|
|
|
|
Novembre
|
0
|
|
|
|
Décembre
|
225
|
|
|
Sources : nous - même
Les rapports  mesurent les variations en plus ou moins des valeurs mensuelles
individuelles par rapport à la moyenne annuelle c'est-à-dire de
combien la valeur de ce mois seront supérieure ou inférieure
à la moyenne. ainsi donc 39,49 pour juillet 2003 indique que la valeur
observée était 60,51% en dessous de la valeur moyenne sur un an
.tout comme le rapport de 69,28 pour août 2003 que la valeur mensuelle
observée était 30,72% inférieur à la valeur moyenne
sur un an. mesurent les variations en plus ou moins des valeurs mensuelles
individuelles par rapport à la moyenne annuelle c'est-à-dire de
combien la valeur de ce mois seront supérieure ou inférieure
à la moyenne. ainsi donc 39,49 pour juillet 2003 indique que la valeur
observée était 60,51% en dessous de la valeur moyenne sur un an
.tout comme le rapport de 69,28 pour août 2003 que la valeur mensuelle
observée était 30,72% inférieur à la valeur moyenne
sur un an.
Il sied alors d'estimer les ventes pour les mois auxquels
certaines données pourtant plus récentes ont été
perdues. Ces données nous sommes vraiment utiles dans l'ajustement de la
méthode des moyennes mobiles par celle de l'usage exponentiel. Ainsi,
nous utilisons la méthode prévisionnelle des moyennes mobiles
pour estimer ces données. Pourtant, l'estimation ne sera possible que si
les conditions actuelles restent invariables sur la période
considérée déterminons de ce fait ; l'accroissement
mensuel de vente qui sera donnée par le rapport 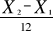 
Tableau XIV : calcul de
l'accroissement mensuel.
|
PERIODE DE 12 MOIS
|
QUANTITE
|
PERIODE DE 12 MOIS
|
QUANTITE
|
|
Juillet 2006
|
5904,18
|
Juillet 2007
|
1086,25
|
|
Août 2006
|
46923,68
|
Août 2007
|
1306,25
|
|
Septembre 2006
|
3776,27
|
Septembre 2007
|
988,125
|
|
Octobre 2006
|
3629,81
|
Octobre 2007
|
1490,42
|
|
Novembre 2006
|
2742,10
|
Novembre 2007
|
3532,88
|
|
Décembre 2006
|
2561,27
|
Décembre 2007
|
4542,50
|
|
Janvier 2007
|
2418,175
|
Janvier 2008
|
5177,08
|
|
Février 2007
|
2112,58
|
Février 2008
|
8208,50
|
|
Mars 2007
|
1950,08
|
Mars 2008
|
5820,00
|
|
Avril 2007
|
1703,42
|
Avril 2008
|
6471,875
|
|
Mai 2007
|
1385,25
|
Mai 2008
|
7106,25
|
|
Juin 2007
|
1200,00
|
Juin 2008
|
7115,625
|
|
TOTAL
|
34269,815
|
TOTAL
|
50439,755
|
|
MOYENNE 1.
|
2855,82
|
MOYENNE 2
|
4203 ,31
|
Source : Nous -même
Accroissement mensuel = 
Cet accroissement signifie qu'il y a une
augmentation mensuelle des ventes d'environ 112,29 kg. D'où, pour
reconstituer les données de six derniers mois de l'année 2008,
nous allons additionner chacune des observations de la tendance par le facteur
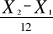 en commençant par la valeur de Juin 2008. en commençant par la valeur de Juin 2008.
Tableau XV : Estimation des
données de Juillet à Décembre 2008
|
MOIS
|
Juillet
|
Août
|
Septembre
|
Octobre
|
Novembre
|
Décembre
|
|
Valeur de la tendance en 2008
|
7227,915
|
7340,205
|
7452,495
|
7564,785
|
7677,075
|
7789,365
|
Source : Tableau fait par nous-
même
Nous constatons que ce pendant quelques limitations de la
méthode des moyennes mobiles :
- Pour calculer une prévision, on est obligé de
stocker les N dernières valeurs observées, et partant la
constitution d'un coût supplémentaire ;
- La méthode des moyennes mobiles accorde un poids
égal à chacune de ces N dernières observations.
Pour pallier à ces problèmes, nous avons recouru
à la méthode de lissage exponentielle qui peut faire le
même travail que les moyennes mobiles sans souffrir de ces deux
limitations. Le lissage exponentiel utilise les ventes de la période en
cours et les ventes lissées.
Nous y reviendrons lorsqu'il faudra faire les
prévisions des ventes.
2°) Détermination des coefficients
saisonniers
Un coefficient saisonnier est une mesure du rapport moyen
entre la valeur mensuelle de la variable et la valeur moyenne annuelle. Il peut
s'interpréter comme mesurant les variations en plus ou en moins des
valeurs mensuelles par rapport à la moyenne annuelle. Pour notre cas, il
se dégage par exemple que les rapports de mars étaient
respectivement de 24,37 en 2004 ; 202,28 en 2005 ; 84,87 en 2006. Ce
rapport varie par suite du contenu aléatoire des valeurs historiques.
Ainsi, pour obtenir une estimation plus ou moins meilleure du
coefficient mensuel qui soit en quelque sorte libéré de ces
fluctuations aléatoires, il faut faire la moyenne de tous les rapports
du mois et appeler ce résultat le rapport typique du mois. C'est ce
dernier qui représente le coefficient saisonnier.
Le tableau ci- dessous donne le coefficient saisonnier
ajusté par retouche de la médiane.
Tableau XVI : Calcule des coefficients
saisonniers des ventes de thé
|
MOIS
ANNEE
|
janv.
|
fev
|
mars
|
avril
|
mai
|
juin
|
juil
|
août
|
sept
|
oct.
|
nov.
|
déc.
|
Total
|
|
2003
2004
2005
2006
2007
2008
|
-
109,13
64,56
-
-
|
198,32
205,94
467,05
-
91
|
24,37
202,28
84,87
668,43
2,06
|
222,9
184,49
292,31
-
385,85
|
-
239,86
72,69
-
338,15
|
270,49
-
-
-
3,09
|
39,49
26,74
30,71
58,17
-
|
69,28
-
26,88
83,11
-
|
-
2,62
-
-
-
|
187,62
190,82
-
163,36
-
|
35,94
-
36,14
62,58
-
|
132,89
80
25,98
106,59
-
|
|
|
Méd.
|
64,56
|
198,32
|
202,28
|
222,9
|
239,86
|
3,09
|
30,71
|
26,88
|
2,62
|
163,36
|
35,94
|
80,00
|
1270,52
|
|
Coeff.
|
61
|
187,3
|
191,1
|
210,5
|
226,5
|
2,9
|
29
|
25,4
|
2,5
|
154,3
|
33,9
|
75,6
|
1200
|
Source : nous-même
Nous pouvons ainsi dire que déterminer le
coefficient saisonnier ou rapport typique du mois, nous divisons chacune
des médianes par la moyenne de ces médianes et ainsi faire en
sorte que le coefficient moyen trouvé pour l'année soit
exactement égal à 100.
Ainsi la valeur du rapport pour chaque mois indique la
relation entre la valeur mensuelle de la variable et la valeur annuelle
moyenne. En rapport à notre tableau de calcul de coefficient
saisonnier, il ressort que l'indice de 61,0 signifie que la valeur de janvier
sera à 39% inférieur à la valeur moyenne ; tout
comme celle de février sera à 87,3% supérieur à la
valeur moyenne.
La gestion budgétaire des ventes sera alors facile par
ce que, pour des raisons de contrôle ces coefficients montreront les
fluctuations qu'il faut attendre de seules causes saisonnières.
3°) Recherche de l'élément
irrégulier
L'indentification de l'élément irrégulier
devient relativement simple partant du tableau de calcul des facteurs
saisonniers, étant donné que le rapport valeur observée et
moyenne mobile sur 12 mois nous a servi dans leur détermination. Nous
partons de la relation suivante pour le calcul de l'élément
irrégulier :
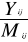 = indice saisonnier x Elément irrégulier = indice saisonnier x Elément irrégulier
Si l'on veut conserver l'élément
irrégulier, il vient :
Elément irrégulier = 
Tableau XVII : calcule des coefficients
saisonniers des ventes de thé
|
MOIS
ANNEE
|
janv.
|
fév.
|
mars
|
avril
|
mai
|
juin
|
juil
|
août
|
sept
|
oct.
|
nov.
|
déc.
|
|
2003
2004
2005
2006
2007
2008
|
-
1,79
1,06
-
-
|
1,06
1,10
2,49
-
0,49
|
0,13
1,06
0,44
350
0,11
|
1,06
0,88
1,39
-
1,83
|
-
1,06
0,32
-
1,49
|
12,012
-
-
-
1,07
|
1,36
0,92
1,06
2,01
-
|
2,73
-
1,06
3,27
-
|
-
1,048
-
-
-
|
1,22
1,24
-
1,06
-
|
1,06
-
1,07
1,75
-
|
1,76
1,06
1,34
1,41
-
|
Source : nous-même
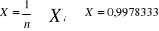

Pour nous assurer que les valeurs contenues dans le tableau ci
haut constituent vraiment l'élément irrégulier, nous
testons l'hypothèse selon laquelle la moyenne arithmétique
ì est égale à l'unité. Mais dans le cas des
données expérimentales nous utiliserons la variance
estimée 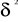 en remplacement de la variance de la population. en remplacement de la variance de la population.
D'où  (avec n= taille de l'échantillon) (avec n= taille de l'échantillon)
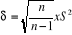 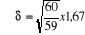 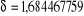
Test de ì
10) H1 : ì = 1
H2 : ì ? 1
2°) Seuil de signification, á = 0,05
3°) n = 60, cas d'un grand échantillon.
L'estimation se fera à l'aide de la loi normale ou loi de normale de
LAPLACE GAUSS.
4°) Rapport critique : rejeter l'hypothèse
nulle si la moyenne arithmétique de l'échantillon n'appartient
pas à l'intervalle de description faite par 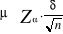
5o) Ainsi nous établissons l'intervalle de
confiance dans lequel nous estimons a 95 % de chance qu'il renferme la
valeur de la prévision sachant que les tables de la loi normale
renseignent au seuil de 5% Z0, 5 = 1,96 ;
Ainsi : X = 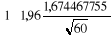
X=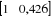
X=
6°) Nous concluons à 95% de chance que les valeurs
du tableau ci-dessus constituent l'élément irrégulier et
constatons que notre moyenne arithmétique de l'échantillon
appartient à l'intervalle. Ce qui veut dire que I est vraiment
l'élément irrégulier de moyenne 1 et d'écart type
1,68.
III.2.2. Elaborations des
Prévisions des ventes
Nous élaborons les prévisions des ventes par la
méthode du lissage exponentiel. Son application nécessite la
connaissance préalable de trois éléments fondamentaux
ci-après :
- les ventes de la période antérieure : Q
t
- les ventes lissées de la période : Q
't
- la constante de lissage : a
La prévision s'établit alors par la
formule : Q t+1 = a . Q t (1-a)Q't
Il sied donc de définir le niveau initial des ventes
lissées ainsi que la constante de lissage. Cette dernière
s'obtient par approximation successive en testant les différents
coefficients compris entre 0 et 1 et en choisissant celui qui donne le
meilleur ajustement c'est-à-dire ce lui qui rend la somme des
carrés des résidus minimale.
Généralement, on prend en considération
trois coefficients a 1 = 0,1 ; a 2 = 0,5 et a
3 = 0,9. Et comme pour la première ligne, il n'existe aucune
provision plus ancienne (c'est-à-dire une ancienne valeur
lissée), il est mieux que nous utilisions dans ce cas, la valeur de la
tendance 2418,175.
Tableau XVIII : lissage exponentiel simple
|
MOIS
|
Valeur de la loi
|
VENTES LISSEES DE LA PERIODE
|
|
A= 0,1
|
A = 0,5
|
A = 0,9
|
|
2007
Janvier
|
2418,175
|
-
|
-
|
-
|
|
Février
|
2112,583
|
2418,175
|
2418,175
|
2418,175
|
|
Mars
|
1950,083
|
2387,616
|
2265,379
|
2143,143
|
|
Avril
|
1703,417
|
2343,83
|
1207,731
|
1969,389
|
|
Mais
|
1385,250
|
2279,818
|
1905,412
|
1730,014
|
|
Juin
|
1200,000
|
2190,361
|
1945,412
|
1419,726
|
|
Juillet
|
1086,250
|
2091,325
|
1422,706
|
1221,973
|
|
Aoûte
|
1306,250
|
1990,818
|
1254,478
|
1099,822
|
|
Septembre
|
988,125
|
1922,361
|
1280,364
|
1285,607
|
|
Octobre
|
1490,417
|
1828,937
|
1134,244
|
1017,873
|
|
Novembre
|
3532,083
|
1795,085
|
1312,331
|
1443,162
|
|
Décembre
|
4542,500
|
1968,785
|
2422,207
|
3323,191
|
|
2008
janvier
|
5177,083
|
2226,156
|
3482,353
|
4420,569
|
|
Février
|
5802,500
|
2521,249
|
4329,718
|
5101,432
|
|
Mars
|
5820,000
|
2849,374
|
5066,109
|
5732,393
|
|
Avril
|
6471,875
|
3146,437
|
5443,055
|
5811,239
|
|
Mais
|
7106,250
|
3478,981
|
5957,465
|
6405,811
|
|
Juin
|
7115,625
|
3841,708
|
6531,857
|
7036,206
|
|
Juillet
|
7227,915
|
4169,099
|
6823,741
|
7107,683
|
|
Aoûte
|
7340,205
|
4474,981
|
7025,828
|
7215,892
|
|
Septembre
|
7452,495
|
4761,503
|
7183,017
|
7327,774
|
|
Octobre
|
7564,785
|
5030,602
|
7317,756
|
7440,023
|
|
Novembre
|
7677,075
|
5282,021
|
7441,270
|
7552,309
|
|
Décembre
|
7789,365
|
5523,326
|
7559,173
|
7664,598
|
|
7901,655
|
5749,930
|
7674,269
|
7776,888
|
Source : Nous-même à l'aide
du tableau XVII
Mais pour savoir le quel des coefficients (0,1; 0,5; 0,9)
utiliser dans nos prévisions définitives, nous évaluons
les erreurs à chaque coefficient afin de voir celui qui minimise la
somme de carrés de ces erreurs.
Tableau XIX : calcul des carres des
erreurs
|
MOIS
|
VALEUR
DE LA LOI
|
a= 0.1
|
a = 0.5
|
a = 0.9
|
|
e
|
e2
|
e
|
e2
|
e
|
e2
|
|
2007
janvier
|
2418,175
|
|
|
|
|
|
|
|
Février
|
2112,583
|
305,592
|
93386,267
|
305 ,592
|
93386,267
|
305,592
|
93386,267
|
|
Mars
|
1950,083
|
437,533
|
191434,689
|
135,296
|
99411,463
|
193,059
|
37271,842
|
|
Avril
|
1703,417
|
640,446
|
410170,972
|
404,315
|
163470,282
|
265,973
|
70741,415
|
|
Mai
|
1385,250
|
894,568
|
800251,892
|
520,324
|
270737,022
|
344,764
|
118862,164
|
|
Juin
|
1200,000
|
990,361
|
980815,292
|
445,412
|
198391,831
|
219,726
|
48279,688
|
|
Juillet
|
1086,250
|
1005,075
|
1010175,903
|
336,456
|
113202,633
|
135,723
|
18420,635
|
|
Août
|
1306,250
|
684,568
|
468632,752
|
-51,772
|
2680,341
|
-206,428
|
42162,410
|
|
Septembre
|
988,125
|
934,236
|
872796,547
|
292,239
|
85403,632
|
297,482
|
88495,675
|
|
Octobre
|
1490,417
|
338,521
|
114596,171
|
-356,172
|
126858,613
|
-472,543
|
223297,306
|
|
Novembre
|
3532,083
|
-1736,998
|
3017162,612
|
-2219,753
|
4927302,274
|
-2088,921
|
4363590,990
|
|
Décembre
|
4542,500
|
-2573,715
|
6624008,961
|
-2120,293
|
4495642,584
|
-1219,309
|
1486713,871
|
|
2008
Janvier
|
5177,083
|
-2950,927
|
8707969,238
|
-1694,730
|
2872109, 279
|
-756,514
|
572313,750
|
|
Février
|
5802,500
|
-3281,251
|
10766606,984
|
-1472,782
|
2169085,623
|
-701,068
|
491496,464
|
|
Mars
|
5820,000
|
-2970,626
|
8224617,308
|
-753,891
|
568351,334
|
-87,607
|
7674,953
|
|
Avril
|
6471,875
|
-3325,438
|
11058539,017
|
-1028,820
|
1058471,412
|
-660,636
|
436439,503
|
|
Mai
|
7106,250
|
-3627,269
|
13157082,954
|
-1148,785
|
1319707,434
|
-700,439
|
490614,188
|
|
Juin
|
7115,625
|
-3273,917
|
10718535,253
|
-583,768
|
340784,610
|
-79,419
|
6307,355
|
|
Juillet
|
7227,915
|
-3058,816
|
9356353,336
|
-404,174
|
163356,460
|
-120,232
|
14455,706
|
|
Août
|
7340,205
|
-2865,224
|
8209509,188
|
-314,377
|
9883,835
|
-124,313
|
15453,769
|
|
Septembre
|
7452,495
|
-2690,992
|
7241436,313
|
-269,478
|
72618,635
|
-124,721
|
15555,407
|
|
Octobre
|
7564,785
|
-2534,183
|
6422081,082
|
-247,029
|
61023,438
|
-124,762
|
15565,590
|
|
Novembre
|
7677,075
|
-2393,054
|
5726708,761
|
-235,805
|
55603,815
|
-124,766
|
15566,608
|
|
Décembre
|
7789,365
|
-2266,039
|
5134932,057
|
-230,192
|
52988,498
|
-124,767
|
15566,710
|
|
SOMME e2
|
|
|
119907803,547
|
|
19409420,315
|
|
8688682,265
|
Source : nous - même à laide
du tableau XVIII
De ce tableau nous constatons que a = 0,9 minimise la
somme des carrés des résidus. Nous l'appliquons dans nos calculs
du lissage exponentiel double.
Notez cependant que l'application de la méthode du
lissage exponentiel simple à une série chronologique comportant
une loi de tendance, donne des résultats inférieurs à la
tendance. Une deuxième application du procédé de ces
valeurs lissées produit des nouvelles valeurs inférieures
à la tendance modifiée. Ce qui fait qu'à la valeur
résultant du lissage exponentiel simple, nous pourrons alors ajouter la
différence entre elle - même et le lissage double puis ajouter
pour tenir compte de la tendance.
L'ajustement montré dans la structure du tableau
ci-dessous, s'est fait de la manière suivante :
1e colonne : Mois
2e colonne : Valeur de la loi
3e colonne : Lissage
exponentiel simple : Q't +1 = a.. Qt + (1-a)
Q't'
4e colonne : Lissage
exponentiel double : Q''t+1 = a . Q't+ (1-a)Q''t'
5e colonne : m =
2Q't+1 - Q''t+1
6e colonne : b= 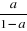 (Q't+1 - Q''t+1) (Q't+1 - Q''t+1)
7e colonne : Valeur de la
tendance ajustée : Qt+1 = m + bn
Appliquées à notre étude, nous dressons
le tableau suivant pour ajuster la méthode de lissage exponentiel en
vue d'établir les prévisions pour l'année 2009.
Tableau XX : lissage exponentiel
double
|
MOIS
|
Valeur
De loi
|
Liss. Exp.
Simple
|
Liss. Exp.
Double
|
Valeur de m
|
Valeur de b (1près)
|
Valeur m+bn
(1près)
|
|
Janvier
|
5177,089
|
4420,569
|
4420,569
|
|
|
|
|
Février
|
5802,500
|
5101,432
|
5033,345
|
5169,519
|
618
|
5782
|
|
Mars
|
5820,000
|
5732,393
|
5662,488
|
5802,298
|
629
|
6431
|
|
Avril
|
6471,875
|
5811,239
|
5796,364
|
5826,114
|
134
|
5960
|
|
Mai
|
7106,250
|
6405,811
|
6344,866
|
6466,756
|
549
|
7016
|
|
Juin
|
7115,625
|
7036,206
|
6967,072
|
7105,340
|
622
|
7727
|
|
Juillet
|
7227,915
|
7107,683
|
7093,622
|
7121,744
|
127
|
7249
|
|
Août
|
7340,205
|
7215,892
|
7203,665
|
7228,121
|
110
|
7338
|
|
Septembre
|
7452,495
|
7827,774
|
7315,363
|
7340,185
|
112
|
7452
|
|
Octobre
|
7564,785
|
7440,023
|
7427,557
|
7452,489
|
112
|
7564
|
|
Novembre
|
7677,075
|
7552,309
|
7539,834
|
7564,784
|
112
|
7677
|
|
Décembre
|
7789,365
|
7664,598
|
7652,122
|
7677,074
|
112
|
7789
|
|
|
7776,888
|
7764,411
|
7789,365
|
112
|
7901
|
Source : tableau fait par
nous-même
Ce tableau montre que l'ajustement b trouvé pour les 5
dernières valeurs est la même que celle de l'accroissement mensuel
rencontrée dans la méthode des moyennes mobiles.
Cette valeur arrondie à 1 près est de +112. Cela
nous pousse à croire que la prévision de la tendance faite
à partir de Janvier 2009 où la valeur de la constante m est
égale à celle de la tendance pour la période de
Décembre 2008, produirait des estimations presque identique à
celle que nous trouverions par la méthode de Trend.
Dès lors, nous appliquerons l'équation de
prévision de la tendance n, période de l'avance, pour
prévoir des ventes en 2009. Cette équation est Qt + n
= m+bn = 7789,365+112 n..
Ce qui revient à dire qu'en court terme, la tendance
des ventes croîtra de 112 kg de thé tous les mois, et 7789, 365
étant l'ordonnée à l'origine c'est-à-dire
décembre 2008.
Considérant que n varie de 1 à 12 et que
l'élément irrégulier égale à l'unité
constante, nous établissons définitivement les ventes
prévisionnelles comme suivent :
Y = Qt + n S.I
Tableau XXI : ventes
prévisionnelles, Exercice 2009 (en kg)
|
MOI
|
Q t+1 = m + bn
|
S.I en %
|
Q t+1 x = S.I
|
|
Janvier
Février
Mars
Avril
Mai
Juin
Juillet
Août
Septembre
Octobre
Novembre
Décembre
|
77.89, 365+(112 x 1)
7789,365 +(122 x 2)
7789,365 +(112 x3)
7789,365 + (112 x4)
7789,365 +(112 x 5)
7789,365 +(112 x 6)
7789,365 + (112 x 7)
7789,365 + (122 x 8)
7789,365 +(122 x 9)
7789,365 +(122x 10)
7789,365 +(122x 11)
7789,365 +(122x 12)
|
61
187,3
191,1
210,5
226,5
2,9
29
25,4
2,5
154,3
33 ,9
75,6
|
4819,83
15009,03
15527,57
17339,65
18911,31
2456,28
2486,28
2206,08
219,93
13747,15
3058,24
6904,82
|
Sources : Nous -même
Le tableau ci-dessus présente les ventes
prévisionnelles tout en tenant compte des fluctuations
saisonnières et irrégulières. Cependant la présence
de l'élément irrégulier risquerait de rendre
imprécises ces prévisions. Nous déterminons de ce fait les
intervalles pour lesquels nous serons sûrs à 99%. Ces intervalles
s'établissent comme suit :
 Qt+n x S.I x Qt+n x S.I x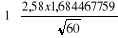
Qt+n x S.I x 
Tableau XXII : détermination des
intervalles mensuels des ventes.
|
Mois
|
Intervalles mensuels des ventes
|
|
Janvier
Février
Mas
Avril
Mais
Juin
Juillet
Août
Septembre
Octobre
Novembre
Décembre
|
[2115,91 ; 7523,754]
[6588,96 ; 23429 ,095]
[6816,60 ; 24238,537]
[7612,11 ; 27067,194]
[8302,07 ; 29520,555]
[107,72 ; 383,038]
[1091,48 ; 3881,083]
[968,47 ; 3443,691]
[96,55 ; 343,311]
[6035,00 ; 2145,301]
[1342,57 ; 4773,913]
[3031,22 ; 10778,424]
|
Source : Nous même
Nous sommes confiant à 99% que les ventes mensuelles de
l'année 2009 seront comprises dans ces intervalles respectifs ainsi nous
avons une chance sur 100 de nous tromper.
Mais, il est important de savoir quelle quantité faut-
il produire afin de satisfaire cette demande de thé. C'est ce qui fait
l'objet du chapitre suivant.
|
|


