Essai de modélisation de la fonction de production dans une entreprise industrielle. Cas du complexe théicole de Butuhe "CTB SPRL" de 2003 à 2008

III.3. RESOLUTION D'UN PROGRAMME LINEAIRE

La résolution d'un programme linéaire doit permettre à déterminer les valeurs des inconnues Xi qui rendent la fonction économique minimum ou maximum. Dans le cadre de notre travail, nous ne voulons pas entrer dans le développement des programmes linéaires. Nous voudrions mettre en application la méthode du simplexe dite algorithme de Dantzing afin de déterminer les quantités optimales de thé sec à produire mensuellement. Cette méthode a comme base les principes ci après :

- Déterminer une première base admissible ;

- Etablir une procédure permettant d'évoluer de base à base ;

- Arrêter la procédure dès qu'il n'est plus possible de diminuer ou d'augmenter la valeur économique suivant le cas de minimum ou de maximum.

La procédure ci-après donne la synthèse de l'application de l'algorithme de Dantzing :

Max [Z=CX] Min [Z=CX]

S/c AX = 0 S/c AX = 0

X=0 X=0

Ces égalités et inégalités constituent un programme linéaire à résoudre suivant les étapes ci-après :

1°) Introduire les variables d'écart pour éliminer les inégalités, c'est-à-dire transformer les inégalités à égalités. Il devient :

Max [Z=CX+0t] Min [Z=CX+0t]

S/c AX + t = 0 S/c AX - t = 0

X=0 ; t=0 X=0 ; t=0

Sachant que t représente la variable d'écart et X la variable de décision.

2°) Chercher la base admissible {t₁, t₂, ... tm}

Si après introduction des variables d'écarts, la base admissible n'est pas trouvée, il faut passer par les variables artificielles V. on crée un situation défavorable pour arriver à une situation favorable. Les variables artificielles V permettent d'avoir une base admissible mais doivent disparaître le plus rapidement possible. Si ces variables artificielles persistent et que le polyèdre soit ouvert, alors la situation est projetée à l'infini.

Max [Z=CX+0t+MV] Min [Z=CX+0t+MV]

X=0; t=; V=0 X=0; t=; V=0

M est un coefficient et tend vers -8 M est un coefficient et tend vers -8

3°) Construction du tableau de simplexe

		Cj	C1	C2...	Ci...	Cn...	?min=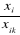 Xik>0	á=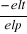	CONCLUSION
Cj	Base	P0	Pk1	Pk2	Pki	Pkn
Coefficient de la fonction économique correspondant aux vecteurs de la base admissible	Vecteurs de la base admissible	b1 b2 ... bi ... bm	a11 a21 ... ai1 ... am1	a12 a22 ... ai2 ... am2	... ... ... ... ...	a1n a2n ... ain ... amm	?1 ?2 ... ?m		Pk entre dans la base admissible ; pr sort de la base admissible
	Zj-Cj	Z0	Z1-C1	Z2-C2	...	Zn-Cn			Pivot=Xrk

4°) Calcul de Z_j- C_j

Pour le problème de maximum, on cherche Z_j-C_j<0. Le vecteur qui en face de max [Z_j-C_j] est susceptible d'entrer et ne peut entrer que s'il existe au moins une des composantes X_ik=0 soit p_k.

Pour le problème de minimum, on cherche Z_j-C_j>0. Le vecteur qui en face de max Z_j-C_j est susceptible d'entrer et ne peut entrer que s'il existe au moins une des composantes X_ik>0 soit p_k.

5°) Quand on ne sait plus entrer les vecteurs dans la base, on a atteint la solution optimale du problème. En face de la colonne ð₀ c'est-à-dire la base, on a des valeurs des variables de décision et les vecteurs qui ne sont pas dans la base sont des variables des valeurs 0 et Z₀ donne la valeur de la fonction économique.