Influence de la dispersion aléatoire faible sur la transmission par solitons et du mélange à quatre ondes dans les fibres optiques

2.3 Modèle de l'évolution du mélange a quatre ondes (FWM) et la condition de résonance [1]

Le mélange a quatre ondes_' nous l'avons déjà dit est un p rocessus non linéaire qui apparait suite aux collisions entre solitons lors du multiplexage en longueur d 'ond e (méthod e WD M). C 'est un p rocessus qui d égrad e la performance de la transmission du signal impulsion véhiculant des informations (données) a travers la fibre op tique. C et effet p eut étre faib le_' mais p eut étre amp lifié de plus en plus que les collisions inter - solitons ont lieu. Pour un cas intégrab le (fibre sans p ertes) de l'équation (2.24) c'est - a - dire g ( z ) = 1 et d ( z ) = ( d) = 1 ' les termes du Mélange a quatre ondes (FWM ) sont connus pour croitre jusqu'à une valeur maximale a p artir d e z --> -. ' ensuite pour décroitre vers zéro quand z --> +. (voir figure 2.2) [4_' 5]. Essentielle ment_' le produit FWM est réab sorb é dans les co mp osantes du soliton aprés que la collision soit compléte.

Pour un cas non idéal d e l'équation (2.2.10) c'est - a - dire g ( z ) # 1 et d ( z ) = ( d) = 1 '

les produits du FWM croissent a p artir de z --> -0. et se saturent a une valeur non triviale (voir figure 2.3) [1 - 5]. Dans ce cas_' un produit permanent FWM interagit avec les impulsions p rincip ales et affecte la transmission du signal dans les systémes WD M .

Tout au long de ce mé moire la L ²- norme d 'une fonction f ( z , t) est d onnée p ar[1_'3] :

f 2 Log.^' f (z , t ) 2 dt ( 2.27)

Nous notons que_' nous p ouvons exp rimer la L ² - norme dans le d o maine d e FOURIER en utilisant le théoréme de PARS EVAL. Nous éb auchons maintenant la dérivation d 'un modele linéaire d 'une équation aux d érivées p artielles qui décrit l'évolution du FWM permanent dans le cas non id éal ( g ( z ) # 1 ) ; en utilisant ce modéle_' nous dérivons une condition d e résonance qui relie la fréquence du soliton s_' l'amplitude A et le pas d 'amplification sans dimension z_a . Nous suivons l'analyse originelle ment p résentée dans les

références [2_' 3].

Nous déco mp osons la solution d e l'équation (2.24) de la maniére suivante :

u ( z , t ) -'="-" u soliton + u FWM oi1 usoliton 7.--. u1 + ^u2 et uFWM -.=-" u112 + u₂₂₁ .

D onc on p eut ecrire que :

u (z,t):=-- u ₁ ( z , t ) + u ₂ ( z , t ) + u ₁₁₂ ( z , t ) + u ₂₂₁ ( z , t) + ( 2.28)

u ₁ ( z , t) et u ₂ ( z , t) sont nos signaux solitons d'entree ayant les frequences resp ectives 51₁ et 52₂. Nous p renons n₂ = -n 1 = n ; cela implique que la difference entre les frequences des signaux est AD = 51₂ - n 1 = 251 ; les termes u 112 ( z,t) et u 221 ( z,t) sont les co mp osantes

resp ective ment Stokes et Anti - Stokes des residus FVVM avec les frequences resp ectives^BB :

n112 = 252₁ - n 2 = -3n et n221 = 2522 -n 1 = 3n donc ⁵²221 = -5 ₁₁₂ .

~

~

~

~

~

~

~

~

~

~

~

1=0 ( 2.29.c)

u 1 + u 2 2 + u * u2 1 1 2

= 0 ( 2.29.d)

Lorsqu'on p rend u ( z , t) de la relation (2.28) et on le place dans l'equation (2.24) on a^B4 :

u₁

2 2

+ 2

u₂

u₁

2 2

+ 2

u 2

1

iu + u g z u

+ ( ) (

1, z 1, tt 1

2

1

iu + u g z u

+ ( ) (

2, z 2, tt 2

2

) 0 2.29.a

= ( )

) 0 2.2

= ( )

9.b

2 2 *

iu 112, z + 1 u 112, tt s-, + 2 ( z )[u ₁₁₂ u ₁ + u ₂ + u ₁ u2

2
1

iu 221, z + 2 u + 2 ( z )

221, tt ..-. [u221

S eule nous interesse la derniere equation (2.29.d)_' celle qui correspond a la dynamique de la co mp osante Anti - Stokes du FVVM : tout si mple ment p arce qu'elle represente suffisamment l'evolution sp atiote mp orelle du Melange a quatre ondes. O n va pour la suite

assimiler u ₂₂₁ ( z,t) a q ( z , t) et on va o mettre le terme en u ₂₂₁ u₁ + u2 2 p arce que celui - ci est négligeable. C e qui conduit a la forme suivante pour l'équation (2.29.d) :

1 = - g

* ( z )u ₁ u ²² ( 2.30)

iqz +q tt

²

C o mp te tenu de la solution (2.26)_' on p eut écrire u₁ et u₂ d e la maniere suivante :

³³ Il s'agit ici de la condition d'accord de phase sans laquelle il n'y a pas apparition du Mélange à quatre ondes.

³⁴ Voir annexe 1

? ~

2

~

( ) (

, = 0 , - ? - ) exp ? - =

j

u _j z t u _j z t j z T j i _j t i z j ,

, 1 2 2.31

( )

~

2

~ ~

avec

A²_;

u j 0 ( z ,t ) = A _j sec h ( A _jt) exp 2

[i ' z (2.32)

oir A ₁= A ₂? A ' T ₁= -T₂ T₀

C e qui nous amene^3D a :

~ u 1 * u 2 2 = A ³ sec h ² [A ( t -52z + T0]sec h [A ( t +52z - T 0 ) ]exp ii [3nt + 1 ( A2 -52²)z 2 ~ ~

g-12 ~

= u 10 u20 exp 3i nt - i z

~ 2 ~

Pour determiner la solution d e l'equation (2.30) on p eut poser que :

q

? 2( z , t ) = H ( z , t)ex43i nt - i 2 z)

(2.33)

O n prend la forme (2.33) qu'on p orte dans l'equation (2.30) et on cherche^3E une equation pour H ( z , t) :

1 [ H _tt + 6 i S2H t - 2(2 51) ² H ] = - g

( z )u 22 0 u 10 ( 2.34)

iH _z +

2

avec

52^2 /44 = u1 * /4 exp - 3i 52t +i z ~ 2

( 2.35)

³⁵ Voir annexe1

³⁶ Voir annexe1

En utilisant la relation (2.34)_' on p eut d ériver la condition d e résonance_' elle relie la fréquence du soliton1 ' l'amp litude A et le pas d 'amplification sans dimension z_a [10]. Pour cela on doit prendre la transformée de FOURIER (T.F) d e l'équation (2.34) :

I 1 T . F iiH z + tt + 6i 52H t - 2(2 5I) 2

^2 H ]} = T. F { -g ( z ) u 22 0 u10 } (2.36)

O n a T . F ( H ) = f He- ^i° dt = H^à . Ainsi la relation (2.36) devient:

-?

oft

iH - 1 0 2

.(2^2 i z ( co, n)H= - à , 2.37.a g z e F z ( ) ( ) 2 ? ( )

+--

2 * 2 * - i t

F z

( )

, = ~

T F u u

. exp 3

( )

- ? ~ =

i t u u

2 1 exp 3

( )

i t e dt

?

? 2.37.b

( )

~ 2 1 ~ ~ - ?

-?

avec

? ? , ? = ? + 6 ? ? + 2 2 ? 2.37.c

2 2

( ) ( ( ) ) ( )

Pour ob tenir la condition de résonance on doit d évelop p er³⁷ F ( z, w) :

?

~ 1 ~ +? - i b

2

( ) ( )

2 - ? - ? +

2 2

F z , ? = A exp ~ i A z i z i T

? ? sec [ ] [

sec 2 ] 2.38

( )

0 ~ h b h b A e ^A db

+ ? 0

~~

2 -?

~

S i l'on re mplace cette expression (2.38) dans l'équation (2.37.a)_' on ob tient :

iH

^z

-

2

1 i [A2 z - ailz +aT0)

( WO =--A ² g (Z)e ² Z sec h ( _2A )I (2 AA₀,_A^w) (2.39)

on ³⁸

³⁷ Voir annexe 1

I ( z , w) = kosh( z) + i wsinh ( z) - exp(i az)]cos ech² ( z) (2.40)

O n introduit le developpement de FOURIER d e g ( z) dans l'equation (2.39) et on l'integre par rapport a z. Il vient :

~ ~ ?i t⁴⁶40 +4) 2 (w)z ) p

z_{w z}

( z, CO) = A ² e sec h (

2A 1E-- g ni ex

(

CO

( 2.41)

)

2+

Pour effectuer l'integration du second me mb re de la relation (2.41) on fait le change ment de variab le suivant : = 52z ' ' dz' = ' ce qui donne :

H

oft

+?

~

z ~ ~g

~

co

n ×

( z, (0) = ² e^i`dT0 sec h (" 2 A lexp (- i ( co² + MD+ 2 ( 2a)²)

2

icn

dce

OD

L

~ ~ ~ ~

? ?

I A

~ ? ~ ~ ~

2 , 2.42

( )

~ ~ ? ~ ~

⁰ A

son	A 2 - 2nka+O(co) (?)= 2.43 ( ) 251

O n constate une grand e contribution d e H^à ( z , ?) lorsqu'on se rapp roche des w_n ' qui

.

2n

sont les racines de p_n (w) = A 2 - 2 nk _a + 0( 0

En effet on a :

?#177; = - ? #177; ? + nk_a - A

2 2

n 3 2 2.44

( )

Pour que H à ( z , ?) soit exp onentielle ment p etit_' il faut choisir la solution positive wn + et la faire tendre vers zero [4] : con + 0 .

³⁸ Voir référence [2, 3]

(0 5.

A 2 27cn

wz I (2 AA0, )dz'

2 -

z a A

La condition de résonance est donc :

2 z_a 2

1 2 n7/- A2 ~

SZ =

( 2.45)

2

₂ (2.46)

R

uFWM

=

usoliton

oil les expressions

uFWM

2

et

u soliton

2

sont prises selon la relation

f

2

+? = ~ -?

f (z , t )

2

dt

.

N otons encore que fréquence du soliton estn ' l'amplitude est A ' la distance entre deux amplificateurs z_a et n est un entier p ositif . Quand z_a = 0,1 et A = 1 ' les valeurs

prédites de n sont : 52 3,95 ; 5 _'59 ; 6_'86 et 7_'92 pour n = 1_' 2_' 3 et 4 resp ective ment. Nous tracons sur la page suivante le ration Mélange a quatre ondes / signal en module élevée au carré. O n le d éfinit par :

2

Figure 2.2 Variation d u rapport R = uFWM2 en fonction d e z cas des fibres sans pertes

u soliton

d(z)=1 et g(z)=1

2

Figure 2.3 Variation d u rapport R = uFWM2 en fonction d e z cas des fibres réelles d(z)=1

u soliton

et g ( z ) # 1 ' z est sans dimension.

Sur la figure 2.2_' on a tracé la variation du rapport R en fonction de z. La forme ob tenue est celle d 'un . pulse . (croissance de -2.5 a 0 et d écroissance symétrique d e 0 a 2.5 suivant z). C ette courb e a été ob tenue en p renant l'exp ression du Mélange a quatre

ond es (FWM) et celle du soliton des fibres sans p ertes [4_' 5]. O n voit b ien que le rapport croit jusqu'à une valeur maximale a p artir de z --> -. ' ensuite pour décroitre vers zéro quand z --> -F. ' en conclusion le Mélange a quatre ondes aprés la collision en z=0 disparait d e lui - méme : on a d onc pas b esoin d e le supp rimer.

Tandis que sur la figure 2.3_' la forme ob tenue est celle d 'un « kink » (forme d 'une marche). L'exp ression du Mélange a quatre ondes (FWM ) est celle d e la relation (2.33) et celle du soliton correspond a la so mme des deux impulsions u1 et u2. O n voit b ien que les p roduits du Mélange a quatre ondes (FWM ) croissent a p artir de z --> -. et se saturent " une valeur non nulle. C e qui signifie qu'ils subsistent méme aprés l'interaction : ceci est néfaste a la transmission des imp ulsions^3H. Dans l'intervalle d e -1 a 1 sur la figure 2.3 on observe des ondulations qui montrent que si la fibre est id éale on retrouve la forme de la figure 2.2.

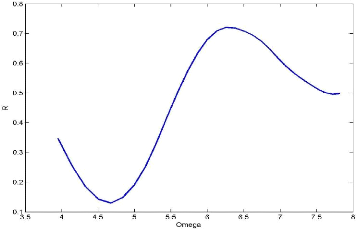
2

Figure 2.4 Evolution du rapp ort R = uFWM 2 en fonction de n ' qui ici est sans

usoliton

dimension.

La figure 2.4 montre la condition d e résonance_' décrite par la relation (2.45). Nous avons tracé ici le rapport R en fonction d en . O n observe (pour notre cas d e figure)

³⁹ Pour remédier à ce problème, on introduit un faible bruit dans le terme de la dispersion (voir chapitre 3).

l'app arition du premier maximum local entre^4K 6 et 6.5. L'exp ression du FWM et celle du soliton sont les mémes que celles de la figure 2.3.

Les figures 2.2_' 2.3 et 2.4 n'ont pas été faciles a ob tenir (surtout les figures 2.3 et 2.4). C eci est dit a la p résence dans les algorithmes corresp ondants_' de plusieurs boucles d 'instructions concernant des sommations discrétes et continues. Pour les figures 2.3 et 2.4_' il fallait attendre un temps d 'exécution b ien long (des heures p arfois une journée !!!) d e l'ordinateur pour avoir au moins une courb e que nous retouchions en modifiant les paramétres du programme⁴¹ avant de le relancer.

Dans le chapitre 3_' nous examinons comment l'équation (2.24) est p erturb ée en présence d 'une dispersion stochastique faib le. Il s'agit de réduire l'amplitude des co mp osantes du Mélange a quatre ondes (FWM) c'est - a - dire celle qui apparait sur la figure 2.3_' de +1 a + 00 suivant z. Pour cela_' nous introduisons d 'ab ord cette dispersion aléatoire dans le modéle et nous regardons comment elle affecte l'évolution des co mp osantes du FWM .

⁴⁰ La prévision est 3.95 pour le premier maximum local, nous comptons améliorer l'approche utilisée.

⁴¹ Voir annexe 2.

C hap itre 3 L 'évolution du FWM et la dispersion

stochastique faible comparée a la dispersion gérée

3 .1 Equation SNL avec la dispersion stochastique faib le [1_'19]

Dans le chapitre p récédent_' nous avons résumé quelques résultats connus concernant l'évolution des co mp osantes du FWM en p résence d e l'amortisse ment / amplification avec dispersion constante. Nous avons dérivé un modéle linéaire d 'une équation aux dérivées p artielles qui d écrit l'influence d e l'évolution d e la co mp osante Anti - Stokes identifiée co mme étant une condition d e résonance qui relie la fréquence du soliton_' son amplitude et la distance entre deux amplificateurs.

Dans un tel systé me_' l'interaction inter impulsions p eut étre étudiée directe ment co mme la dynamique d 'une p aire de solitons. Les solitons sont connus pour survivre a une telle interaction avec seule ment un change ment dans les paramétres co mme la phase. C 'est une conséquence directe d e l'intégrab ilité [15]. Tout systéme de communication réel_' cep end ant_' va voir apparaitre en son sein des effets physiques qui détruisent cette structure intégrab le. Le cas échéant on a l'atténuation et l'amplification requise pour annihiler celle - ci_' cela méne a un systéme non - intégrab le dans lequel les effets du mélange a quatre ond es sont manifestes [1 - 4].

Nous examinons maintenant l'évolution du mélange a quatre ond es en p résence d 'une faible dispersion stochastique a travers des simulations numériques.

Nous consid érons une version modifiée de l'équation (2.24) :

d z ( ) ( ) iu + u + g z z tt 2

u

2 u = 0

( 3.1)

oft d ( z) représente maintenant un terme de dispersion qui varie stochastique ment :

d ( z ) = ( d) + ( z) (3.2)

Ici ( d ) = 1 et ( z) est un terme du bruit b lanc gaussien donné co mme suit :

((z)) = ⁰ ' (?( z ),( z' )) = D8( z-z ') (3.3)

oft D d énote le paramétre intensité du bruit. G énérale ment les valeurs de D sont rangées entre 0_'005 et 0_'05. Dans notre analyse_' nous nous intéressons a la faib le dispersion stochastique qui est définie ici co mme le cas oft D << 1 dans les équations (3.2) et (3.3).

Il a été montré aup aravant [10]_' que la distance a laquelle le signal d 'entrée commence a se d égrad er sous les effets de la faible dispersion aléatoire est inverse ment p rop ortionnelle " l'intensité du b ruitD .

C ette distance d e dégradation est d éfinie par :

z deg r

1 ? D (3.4)

oft z _deg r = 20 - 200 correspond a notre intervalle de valeurs d e D .