Annexe 2
2.1 L'effet KERR [18]
La rép onse d 'un matériau
diélectrique est non-lineaire pour un champ électro
magnétique tres intense. L'indice de réfraction
devient : n = n1 +
n2I oh.
n1 représente l'indice classique et
n2 est l'indice non-lineaire (a ne pas
confondre avec l'indice de la gaine). I est l'intensité dans la
fib re' exprimée en W
/ m2 .
Pour ce qui est des fibres optiques mono
modes' la valeur de n2 est
relative ment faib le dans la silice'
l'intensité est tres élevée' car la puissance
est confinée dans le coeur de fiab le dimension. O n a
une grand e distance d 'interaction' grace au
phénomene de guidage et une atténuation tres faib le
(0'2 dB/km a 1'55 pm)
2.2 Description breve de la méthod e
utilisée pour la réalisation d e certaines simulations (courbes)
présentes dans ce mémoire
2.2.1 " AlgorithmeCE " de la simulation
numérique d e la courb e (figure 2.3)
On veut q ( z , t ) = u221
= uF solution de l'équation :
* ( z ) u 1 u 22
( 2.30)
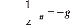
iqz +
1
2q
2
u
Pour tracer ( )
R = FWM = f z
2
' ilfaut " q " et u soliton

u soliton
usoliton ?u1
+u2
. 1 11
u 1 ( z , t )= A
sec h[ A ( t + - T 0 )]
expit[- nt +
vt2 - n2
mil
2
111
u 2 ( z , t ) = A
sec h[ A ( t - + T0 )]
expii[nt + (
A2 - n2
mil 2 C o mme A=1 '
T0 =0 '
z
[ ] ( )2
i 1 -? 2
i t
u sec ( )
- ? - ? + sec ( )
+ ? ?
i t
? + =
u u h t z e h t z e e
soliton 1 2

2

O r co mme
( z, t)
( , )
z t
dt
f
f
f+oo
J-00
= -
g
46 Pas au sens où l'entendent les
informaticiens, il s'agit juste ici des diverses étapes dans la
réalisation des simulations.
~usoliton 2 = [
sec h( t - 51z)
e-iat + sec h( t +
51z)e iat ]× [ sec
h( t - 51z)e -iat
+ sec h( t + 51z)e iat ]*
~ usoliton 2 = [ sec h(
t - nz)e -iat + sec
h( t + 51z)e
iat]× [ sec h( t -
51z) e iat + sec h(
t + 51z)e -iat]
~ usoliton
( t - 51z) + 2 sec h
t z h t z
- ? sec ( ) cos( ) sec ( )
+ ? ? +
t h t z
2 + ?
( )
2
2
sec
h
=
|
~ usoliton
|
2 + ? 2 +?
= u dt
soliton
~ = ~
-? -?
|
[sec h22( t t---5z))+ +2
2sec ch( t t--- 5z ))sec ch( t t++
5z))cos((5t ))++secch22( t
t++5z)]dtt
|
Pour q ( z , t ) = u221 =
u FWM on a
? ~( z , t ) = =H
H( z , t)exx3i it t- i
22zz
2.33))

q
2
2
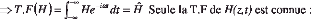
+?
~ z ~
~g~
--co
nn×X
i ir 2
à
H
~ ~ ~
?? i 2
0
( ) ( ( ) )
2
z , ? e i ? T
= sec h ~ ~ ~ -
exp ? ?
+ ? + ?
8 2 2
? ~ ~ ~
2 A 2
5n.
zz
((05.
ddee
OD
L
~ ~ ~ ~
? ?
I A
~ ? ~ ~ ~
2 , 2.42
( )
~ ~ ? ~ ~
0 A )
Avec I ( z , co) =
kosh( z) + i wsinh ( z) -
exp(icoz)]cosech2 ( z)
·
A 2 - 2 nk + cD( w)
a? ( ? ) ?
252
n
( (c, ,5)= ( (2 + 66(01+ 2 ( 2 25)2)
) 2.37.a))
On doit trouver d'a bor H à (
z , w) ensuite', on cherche
H(z't) ' puis on déterminee
? 3i
2 ~
H(z, t ) ) 2
q ( z, t) 2 = H (
z, t) exp
2
i
t
t
i i
2
2
2
=
|
Ensuite
|
+.0q ( z , t)
)2 2= = j q(z , t )
)22dtt== fH( z
,t) -?
)
|
2
|
dt
|
2
u
Pour prendre enfin le rappor ( )
R = FWM = f z
2 )
usoliton


| 


