2.2.2 « Algorithme » de la simulation
numérique de la cour be (figure 2.4)
Ils'agitt ici du cas des fibres réelles casoùt
d(z)=1 et g ( z ? 1 , ontrace e
~T . F H
( ) = f dt = Hà Seule la T.F de H(z,t) est connue : -?
2
R= uFWM 2 = f( SI) pour un zfixe;
;
usoliton
Ici on fait varier maintenant 52 , suivant l'expression :
=
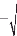
1 2 n 7t- A2
~ - ~
2 za 2 ~
( 2.45)
Nous avons juste modifier le programme précédent
celui de la figure 2.3) : maintenant n va de 1 à 4.
2.2.3 Algorithme » de la simulation
numérique de la courb e (figure 3.1)
N ous avons discrétisé p artielle ment sur
la variable t » l'équation :
|
d
iu z +
|
( z) u tt + g (
z)
2
|
u
|
|
2
u = 0
|
( 3.1)
|
+?
d ( z ) =
(d) + ( z) ,
(d) = 1 ,
((z)) = 0 ,
((z)(z')) =
Dö(z - z ') , g( z ) =
E g exp( - inkaz)
n=-.
O n a p osé que u ( z
, t ) = X (z , t ) + iY
(z , t )
) = 0
+
L
?
iX z - Yz +1 2 (Xtt +
iYtt ) + g(z )( X 2
+ Y2 )(X +iY On obtient le système
suivant :
+co
-
Yz +
0
=
)]
Xtt + 1 Xtt +E 2
(X 2 + Y 2 )[( X -
na-Y)cos(20 7inz ) + (n7rX + Y) sin(
207inz

1
2

n
=-?

(1)
1
Ytt + 2Ytt
1 +E2 2 +
Xz +
?
2
+.0
n
=-?
Y2) [-(
0
=
)]
X n Y
- ? ) sin( 20 ? nz
) + (nzX +
Y)cos(207inz
2 1+ n2 71-
On discrétise Xtt et
Ytt selon les différences finies centrées
:
X z X z X z
- +
+ 1 ( ) 2 ( ) 1 ( )
j j j -
X z t
( , ) =
tt
( ) 2
? t Y z Y z Y z
-
j + 1 ( ) 2 ( ) ( )
+
j j 1
, 2
Y z t
( , ) = -
tt (
) ? t
}
~~
+o
On pose pour la deuxième équation de ce
système
1 1f 1 ( z , t) = -
Ytt+ L 2 2 (X
2 + Y 2 )[(niff+Y) cos(20
n7z) - (X - na-Y)sin( 20
n71z)]
2 =-00 1 n 71-
Donc
+ex,
2( At ) n= -pp 1 + n
x-1 1
2 + 2a 2 2 [ X.2 /
(z ) +Yj2
?

Y z Y z Y z
( ) 2 ( ) ( )
- +
j
f1,
j + 1 j j - 1
( )
) +
z = - { (z )] [ -( X ( z )
- itnYj (z)) sin(2070nz
( nizX (z ) + Y(z))
cos(207inz
j
j
1 Y z Y z Y z
( ) 2 ( ) ( )
- +
j + 1 j j 1
Et on pose ( , )
g 1 ( z , t ) = - Y
tt z t donc g z
( ) = - -
1 , j
2( At)2
D e mê me on a p our la pre miere équation
:
f2( z ) -{ X
1 (z ) - 2 Xj (z
)+ X -1j(z) +0. 1

=
( )][( ( )
- ? ( )) cos( 20 ? nz
z X z nY z
j j
) +
2 2 2 [ X.2 /(z
)+Y
2(
A
t ) n=-
co
1+n
)] }
( (z ) + Yj (z))
sin(202nz
n2tX
(2)
(3)
(4)
g 2 , j ( z) = (z ) - 2
X (z ) + (z)
2( At) 2
C e qui signifie que le systè me ED P precedent
se ramène a un système S D E ordinaire :

dX z
j ( ) =
dz
dY z
j ( ) =
dz
( )
z + ? ( )
z g z
j ( )
1 , j
( )
z + ? ( )
z g z
j ( )
2 , j
f 1 ,
f 2 ,
~
O n est dans un cas typique S D E d éjà
résolu d ans la reference [19] :
X k =X k,
z z
+ ? z z
k +?

'
z dz
' )
(
'
z dz
' )
k
+ ~ f z dz
( ' ) ' + ~ ? ( )
z g
'
j z 1 , j 1 , j
z
k k
(
z z
+? z z
k +?
Yk +1, j = Yk
k
+ ~ f z dz
( ' ) ' + ~ ? ( )
z g
'
j z 2 , j 2 , j
z
k k
Lorsqu'on s'intéresse d 'ab ord a première
equation de ce dernier systè me :

'
? z
~
~~
)
~
~~
)
? f z
(
1 , j
( )
z z
' - k
z k
( )
z z
' - k
z k
~
~~
'
+
+
( ' )
z g z
= ( )
j 1 , j k
+
g1,
~
L
( ' ) ( )
z f z
=
j 1 , j k
f1,
+
'
z
(
1 ,
? g
j
'
? z
~
~~
O n re mplace ces expressions d ans la première
equation du systè me (3) on aura
X k + 1, j = X k,j f1, j
(z k)Az
~
~~
+
? f z
j (
'
) ~ z z
+? z z
+?
k
1 , k
~ ( ' ) ' ( )

z z dz g z
- + ~ ? ( )
z dz
' ' +
k 1 , j k
z k zk
a
z '
z k

z
+Az
)
j
ag
1,
zk
az
zk
'
? ( z')( z ' -z k
Par analogie on écrit pour la d euxiè me
equation du système (3) :
§ f2, j (zk)Az ,
Yk
Yk
j
1,
~
~~
+
? f z
j (
'
)
~
~~
z z z z
2 , k +? k +?
~ ( ' ) ' ( )
? z
z z dz g z
- + ~ ? ( )
z dz
' ' +
k 2 , j k
z k zk
'
z k

z
+Az
)
j
ag
2,
az
fzk
zk
zk
?( z')(z '
-zk ) dz '
O n sait que :
z k +Az
a) Le terme Az ')(z'-z
k )dz' est d e moyenne nulle et de fonction d
e correlation :
f
z k
<
z k
~ z k
+Azz z
' '
>
)dz
l +?
? ( )( )
z z z dz
' ' - '
· ? ( )(
z z z
' ' ' ' -
k k
~ z l
+Az
=
fzl z l
D8kl
3
( )
? z
( )
z z dz D
2
' - ' = ?
k kl
3
3
ez k+Az
D c jAz ')(z ' -z k
)dz' est d 'ordre ( Az ) 2
zk
b ) Le terme
fzk +Az
J 4.( z
)d.Z est de moyenne nulle et de fonction de corrélation
:
Z,
<
z k
~ z k
' '
>
)dz
+Azz z
l +?
? ( )
z dz
' '
· ~ ? ( z ' '
+Az
=
1zlz
l
Db.kl
)
z l
1
2 .
dz'= D 8kl Az
rzk+Az
Alors jg ( z ' )dz
' est d 'ordre ( Az )
k
z
D e ces d eux termes on va négliger celui qui d
'ordre sup érieur a Az a savoir f
z k+Az ( z ')( z '-
z k )dz' .
z k
D 'o11notre systè me de S D E (3) se résume
a :
~ ~~
~~
(5)
X =k 1 , j X k, j ,j
(z k ) Az+ g
1(zk)71k
Yk +1, j = Yk , j +
f2,j (z k) Az+ g2,
j z k )'7k
z k+Az
O11 k = f (
z')dz' < 77k
·
171 >= DgkiAz ce qui signifie
que 17k = DAz
· rk rk est nombre
k
z
aléatoire gaussien de moyenne 0 et de variance
1.
O n numérise le systè me (5) en prenant
pour différentes valeurs d e l'intensité du bruit
D = 0,005 - 0.0 1 - 0.03 - 0.05 sur l'intervalle
de 0 a 2.5 d e z.
| 


