8.2.2.
Vérification de la première hypothèse de
recherche(HR1)
1. Formulation des hypothèses alternative
(Ha)et nulle (H0)
HR1: L'imposition des mesures de l'ordre
urbain suscitela résistance au changement des commerçants de
trottoirs.
H0 : Il n'existe
pas de relation de dépendance entre l'imposition des mesures de l'ordre
urbain et la résistance au changement des commerçants de
trottoirs.
Ha: Il existe une relation de
dépendance entre l'imposition des mesures de l'ordre urbain et la
résistance au changement des commerçants de trottoirs.
2. Présentation du tableau de contingence:
Tableau croisé dynamique des deux variables de cette hypothèse de
recherche.
L'élément fondamental du tableau croisé
est le nombre d'occurrences dans chaque cellule du tableau. La
procédure statistique qui est employée pour tester
l'hypothèse nulle compare les occurrences observées avec les
occurrences attendues.L'occurrence attendue est simplement la fréquence
que l'on devrait trouver dans une cellule si l'hypothèse nulle
était vraie.
Tableau 6 :
Récapitulatif du traitement des observations pour HR1
|
|
Observations
|
|
Valide
|
Manquante
|
Total
|
|
N
|
Pourcent
|
N
|
Pourcent
|
N
|
Pourcent
|
|
Imposition des mesures
X
Résistance au changement
|
164
|
97,6%
|
4
|
2,4%
|
168
|
100,0%
|
On observe dans le tableau6 que pour l'enquête qui a
été menée, 164 participants ont donné une
réponse aux items Q13, Q14, Q15 relative à l'imposition des
mesures. Cela représente 97,6 % de l'échantillon. Le test sera
donc basé sur ces observations.
Tableau 7: Tableau
croisé imposition des mesures et résistance au changement
|
|
Résistance des commerçants au
changement
|
Total
|
|
Très forte
|
Forte
|
Faible
|
Très faible
|
|
Imposition des mesures de l'ordre urbain
|
Forte intensité
|
Fo
|
47
|
41
|
30
|
12
|
130
|
|
Fe
|
39,6
|
40,4
|
35,7
|
14,3
|
130,0
|
|
%
|
36%
|
32%
|
23%
|
9%
|
100%
|
|
Intensité moyenne
|
Fo
|
3
|
7
|
12
|
2
|
24
|
|
Fe
|
7,3
|
7,5
|
6,6
|
2,6
|
24,0
|
|
%
|
13%
|
29%
|
50%
|
8%
|
100%
|
|
Faible intensité
|
Fo
|
0
|
3
|
3
|
4
|
10
|
|
Fe
|
3,0
|
3,1
|
2,7
|
1,1
|
10,0
|
|
%
|
0%
|
30%
|
30%
|
40%
|
100%
|
|
Total
|
|
50
|
51
|
45
|
18
|
164
|
Selon le tableau7, on remarque que 36% de ceux qui
perçoivent une forte intensité de l'imposition des mesures
résistent très fortement au changement.Alors que 13% de ceux qui
perçoivent une intensité moyenne de l'imposition résistent
très fortement et 0% de ceux qui perçoivent une faible
intensité de l'imposition des mesures résistent très
fortement au changement.
Figure 21 :
Diagramme à barres du tableau croisé de HR1
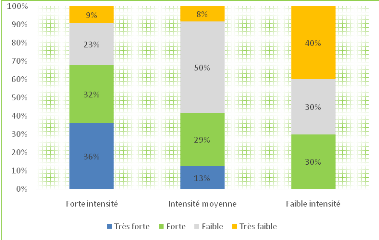
Ce résultat est celui d'un seul échantillon et
en lui-même, il est peu intéressant. Par conséquent,
on veut savoir ce que l'on peut conclure au regard de la population en
partant des résultats de l'échantillon. Il est donc question
de tester l'hypothèse nulle selon laquelle, dans la population, la
résistance évolue indifféremment de l'intensité de
l'imposition des mesures.
Il faut donc calculer la statistique du Khi-2 à partir
de la différence entre les occurrences observées (fo) et les
occurrences attendues (fe). Le SPSS offre ces résultats dans le tableau
7. On remarque que les fréquences théoriques ou attendues (fe) se
distinguent des fréquences observées (fo) dans
l'échantillon. S'il n'y avait pas de relation entre les deux variables,
les fréquences observées et les fréquences
théoriques seraient identiques. Mais la différence est-elle
significative?
Le tout peut être évalué à partir
de la statistique Khi-2.Nous devons faire la somme de chaque résidu
(occurrence observée - occurrence attendue) mis au carré
divisé par l'occurrence attendue, tel qu'indiqué dans la formule
suivante :
÷2 = ? 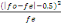 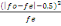
Où fo= fréquence observée, fe=
fréquence théorique et -0,5= correction de Yates
3. Résultats du Khi carré pour
HR1
Le résultat est positionné dans une distribution
de Khi-2 ajustée en fonction du degré de liberté (nombre
de rangées - 1) x (nombre de colonnes - 1).Le SPSS donne les
résultats dans le tableau suivant :
Tableau 8 :
Résultats du Khi carré pour HR1
|
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
20,572a
|
6
|
,002
|
|
Rapport de vraisemblance
|
20,352
|
6
|
,002
|
|
Association linéaire par linéaire
|
13,798
|
1
|
,000
|
|
Nombre d'observations valides
|
164
|
|
|
|
a. 5 cellules (41,7%) ont un effectif théorique
inférieur à 5. L'effectif théorique minimum est de
1,10.
|
4. Décision pour HR1
Pour á= 0.05, on observe que le degré de
signification qui est de 0,002 est très bas, ce qui indique que les
différences entre les occurrences observées et attendues sont
significatives. Concrètement, cela veut dire que l'on retrouverait ces
différences 2 fois sur 1000 (0,2 sur 100) si l'hypothèse nulle
était vraie.
En d'autres termes, X2cal=20,572 =
X2lu=12,59.
On doit donc rejeter l'hypothèse nulle(H0)
selon laquelle Il n'existe pas de relation entre l'imposition des mesures de
l'ordre urbain et la résistance au changement des commerçants de
trottoirs. L'hypothèse alternative (Ha) est retenue.
C'est-à-dire qu'il existe une relation significative entre l'imposition
des mesures de l'ordre urbain et la résistance au changement des
commerçants de trottoirs.
Le coefficient de contingence (C) est égal à
0,334. Ce qui signifie que l'effet de l'imposition des mesures sur la
résistance au changement est de taille moyenne.
À partir de ce résultat et de la lecture
de la figure21, on peut dire qu'il y a une relation d'influence de l'imposition
des mesures sur la résistance au changement. En effet, on constate que
le nombre de ceux qui résistant très fortement augmente au fur et
à mesure que l'intensité de l'imposition des mesures augmente.
Dans l'échantillon donc, plus l'intensité d'imposition des
mesures est perçue comme forte, plus la résistance est forte.
On conclut donc que l'hypothèse HR1 est
confirmée c'est-à-dire que « L'imposition des
mesures de l'ordre urbain suscite la résistance au changement des
commerçants de trottoirs ».
| 


