2.4 Modèle de Garman-Kohlhagen
Le modèle Garman-Kohlhagen est une modification du
modèle d'évaluation des options de Black-Scholes. Il a
été proposé en 1983 par Garman et Kohlhagen. Ils ont
modifié le modèle Black-Scholes de manière à ce que
le modèle puisse faire face à la présence de deux taux
d'intérêt sans risque. La différence avec le modèle
BS est que le modèle GK corrige la différence entre les taux
d'intérêt domestiques et étrangers. En même temps, le
modèle Garman-Kohlhagen partage les mêmes limites que le
modèle Black-Scholes.
Le modèle Garman-Kohlhagen traite les devises
étrangères comme s'il s'agissait de titres de placement qui
fournissent un rendement en dividendes connu. Le propriétaire de la
devise étrangère (domestique) reçoit un rendement en
dividendes égal au taux sans risque du pays étranger
(domestique).
Notons S le taux de change actuel (la valeur d'une
unité de la devise étrangère mesurée en devise
domestique). S est supposé suivre un mouvement Brownien
géométrique semblable à celui des actions. Dans l'univers
risque-neutre, la dynamique du processus s'écrit:
dS = (rd - rf)Sdt + óSdz (2.14)
En suivant les même démarche de la section
précédente, on aboutit à l'équation aux
dérivées partielles suivante
? f + (rd - rf)S ? f ?S2 = rd f
(2.15)
?S + 1 2ó2S2
?2 f
?t
Les valeurs d'un call Européen ou d'un put
Européen sur devise deviennent: c = S0e-rf
TN(d1) - Ke-rdTN(d2) (2.16)
p = Ke-rdTN(-d2) -
S0e-rf TN(-d1) (2.17)
avec:
d1 =
ln(S0/K) + (rd - rf +
ó2/2)T
/
ó T
et :
|
d2 =
|
ln(S0/K) + (rd - rf -
ó2/2)T
|
/
= d1 - ó T
|
|
|
|
|
16
Le taux d'intérêt domestique, rd, et le
taux d'intérêt étranger, rf, sont tous deux des
taux continus pour la maturité T. Le put et le call sur une
devise sont symétriques. De ce fait, un put permettant de vendre la
devise A au taux de change K est équivalent à un call
permettant d'acheter la devise B au prix 1/K.
17
2.5 Les lettres grecques
Une institution financière qui vend une option
à un client est confrontée au problème de gestion de son
risque. L'institution financière doit donc neutraliser son exposition au
risque du marché afin de ne pas subir des pertes importantes dans le cas
où le client exerce cette option.
Les stratégies les plus sophistiqués
utilisées par les traders, nécessitent le calcul de mesures
telles que le delta, le gamma et le vega. Ces mesures sont communément
appelées lettres grecques. Elles quantifient différents
aspects du risque dans une position sur options.
Cette section examine les propriétés de
certaines lettres grecques les plus importantes. Pour calculer une lettre
grecque, il faut utiliser un modèle de valorisation d'option. Les
traders retiennent le modèle de Black-Scholes ou ses extensions, dans
notre cas le modèle de Gar-man-Kohlhagen, pour les options
Européennes.
2.5.1 Delta
Le delta d'une option est défini comme le taux de
variation de la valeur de l'option par rapport à celle du sous-jacent.
C'est la pente de la courbe reliant la valeur de l'option à celle du
sous-jacent. La figure 2.2 montre la relation entre la valeur du call et le
cours du sous-jacent. Lorsque 1e cours du sous-jacent est au point A, la valeur
de l'option est au point B, et est la pente de la tangente indiquée dans
la figure.
Plus généralement:
?c
= ?S
Pour un call Européen sur devise, on peut montrer que:
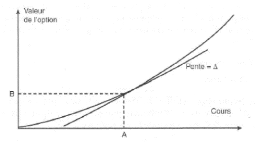
FIGURE 2.2 - Représentation du delta, [14].
(c) = e-rf
TN(d1)
où d1 est défini dans l'équation
(2.16).
Pour un put Européen sur devise, le delta est égal
à :
(p) = e-rf
T(N(d1) - 1)
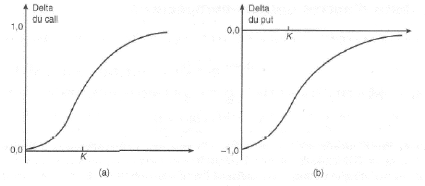
La figure 2.3 montre les variations du delta d'un call et d'un
put en fonction du cours du sous-jacent.
18
FIGURE 2.3 - Variation du delta en fonction du cours du
sous-jacent: (a) option d'achat; (b) option de vente, [14].
| 


