Le marché de change marocain. évaluation et couverture des options européennes et américaines de change et modélisation du taux de change du dirham.

2.5.2 Gamma

Le gamma d'un portefeuille d'options, noté F, est le taux de variation du delta du portefeuille en fonction de la valeur de l'actif sous-jacent. C'est la dérivée seconde de la valeur du portefeuille par rapport au cours de l'actif:

?²Ð

F = ?S2

Si le gamma est faible, le delta varie lentement, et il n'est pas nécessaire d'ajuster fréquemment le portefeuille pour maintenir un portefeuille delta-neutre. Par contre, si le gamma est important en valeur absolue, le delta est très sensible aux variations du cours de l'actif sous-jacent. Il est alors risqué de laisser un portefeuille delta-neutre inchangé trop longtemps.

Pour un call ou un put Européens sur devise, le gamma s'écrit:

N0(d1)e-rf T

F = v

S0ó T

où d1 est défini dans l'équation (2.16). Et N'(x) par:

1

N'(x) = v2ð e-x2/2 (2.18)

Le gamma est toujours positif, la figure 2.4 montre les variations du gamma en fonction du cours du sous-jacent.

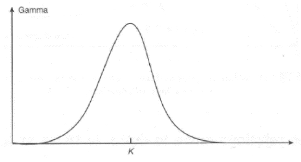
FIGURE 2.4 - Variation du gamma en fonction du cours du sous-jacent, [14].

2.5.3 Thêta

Le thêta d'un portefeuille d'options, È, se définit comme le taux de variation de la valeur du portefeuille par rapport à la durée de vie de l'option.

Pour un call Européen sur devise, le thêta s'écrit:

v

2 T

Pour un put Européen sur devise, on obtient:

È(c) =

-S0N0(d1)óe-rf T+ rfS0N(d1)e-rf T - rdKe^-rd^TN(d2)

19

È(p) =

-S0N0(d1)óe-rf T	rfS0N(-d1)e-rf ^T+ rdKe^-rd^TN(-d2)

où d1 et d2 sont définis dans l'équation (2.16) et N⁰(x) dans l'équation (2.18).

Le thêta d'une option est généralement négatif car la valeur de l'option diminue lorsqu'on se rapproche de l'échéance. La variation du thêta en fonction du cours du sous-jacent, pour un call, est illustrée dans la figure 2.5.

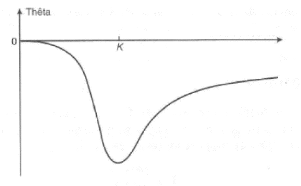
FIGURE 2.5 - Variation du thêta en fonction du cours du sous-jacent, [14].

20

2.5.4 Vega

Nous avons supposé, jusqu'à présent, que la volatilité du sous-jacent reste constante pendant toute la durée de vie de l'option. En réalité, c'est loin d'être vrai car la volatilité varie au fil du temps. Cela signifie que la valeur de l'actif dérivé est susceptible de changer à cause des variation de la volatilité.

Le vega d'un portefeuille de d'options, y, représente le taux de variation de la valeur du portefeuille en fonction de la volatilité de l'actif sous-jacent:

y =

aÐ

acr

Si la valeur absolue du vega est importante, la valeur du portefeuille est très sensible au moindre changement de volatilité. Si le vega est faible, en valeur absolue, un changement de la volatilité n'aura qu'un léger impact sur la valeur du portefeuille.

Pour un call ou un put Européens sur devise, le vega est obtenu par:

v

y = S0 TN0(d1)e-rf T

où d1 est défini dans l'équation (2.16) et N'(x) dans l'équation (2.18).

Le vega d'une option est toujours positif. La variation du vega en fonction du cours du sous-jacent est illustrée dans la figure 2.6.
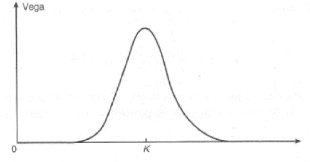