1.3 Notions sur le pricing des options sur devises
Avant de se lancer dans les différent modèle de
pricing des options sur devises, il faut avoir une bonne compréhension
des facteurs et des paramètres qui déterminent le prix de ces
options. En effet, le prix d'une option ne dépend pas uniquement du gain
obtenu en décidant de l'exercer immédiatement, mais aussi, de la
probabilité que cette option devienne bénéfique. De ce
fait, la valeur d'une option se décompose en deux éléments
: La valeur intrinsèque et la valeur temps.
Prix de l'option = Valeur intrinsque
+ Valeur temps
1.3.1 Valeur intrinsèque
La valeur intrinsèque correspond à la valeur
minimale de la prime; elle correspond au gain immédiat, sans risque, que
ferait l'acheteur de l'option en faisant simultanément une
opération sur le marché des changes (le marché au comptant
ou le marché à terme).
La valeur intrinsèque représente la
différence entre le prix d'exercice et le cours à terme, pour une
option Européenne, et la différence entre le prix d'exercice et
le cours le plus avantageux des cours au comptant ou à terme, pour une
option Américaine. Lorsque cette différence est négative
la valeur intrinsèque est nulle. Le tableau ci-dessous présente
les différentes valeurs intrinsèques selon les types
d'options:
9
TABLE 1.3 - Les différentes valeurs intrinsèques
selon les types d'options.
|
Type
Positon???Call
|
|
Put
|
|
Achat
|
Max(ST - K; 0)
|
Max(K - ST; 0)
|
|
Vente
|
-Max(ST - K; 0)
|
-Max(K - ST; 0)
|
1.3.2 Valeur Temps
La valeur temps reflète la probabilité que
l'option devienne dans la monnaie. Elle est égale à la
différence entre le prix de l'option et sa valeur intrinsèque.
Comme cela a été évoqué dans la
section précédente, le prix des options de change est en
général fonction de 6 paramètres. Dans cette section, nous
nous intéressons à ce qu'il advient du prix des options lorsque
l'un de ces facteurs change, tandis que les autres restent constants. Les
résultats sont résumés dans le tableau ci-dessous :
TABLE 1.4 - Résumé des effets de l'augmentation
d'une variable, lorsque les autres restent fixes, sur le prix des options sur
devises.
|
Variable
|
Call
|
Put
|
|
Taux de change au comptant
|
+
|
-
|
|
Prix d'exercice
|
-
|
+
|
|
Date d'échéance
|
+
|
+
|
|
Taux d'intérêt sans risque domestique
|
+
|
-
|
|
Taux d'intérêt sans risque étranger
|
-
|
+
|
|
Volatilité du taux de change
|
+
|
+
|
"+" signifie qu'une croissance de la variable provoque une
augmentation de la valeur de l'option. "-" signifie qu'une croissance
de la variable provoque une baisse de la valeur de l'option.
Taux de change au comptant et prix d'exercice
Si une option d'achat est exercée à une date
future, le flux engendré, appelé Payoff, est égal
à la différence entre le taux de change au comptant et le prix
d'exercice. Par conséquent, la valeur d'un call augmente lorsque le taux
de change croît. Elle est faible quand le prix d'exercice est
élevé. Pour une option de vente, le Payoff à
l'exercice est égal à la différence entre le prix
d'exercice et la taux de change. La valeur de ce type d'option diminue si le
taux de change s'accroit. Elle augmente au contraire, lorsque le prix
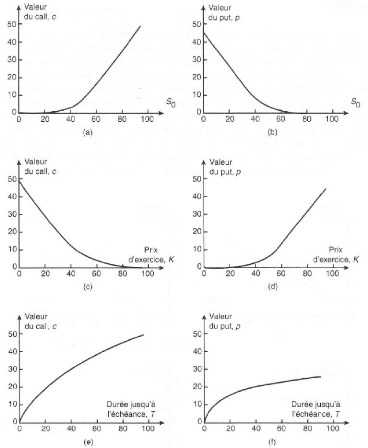
d'exercice est élevé. Les graphiques a, b, c, d de la figure 1.1
illustrent la façon dont les valeurs d'un call et d'un put
dépendent du taux de change et du prix d'exercice.
Date d'échéance
Étudions à présent les effets de la date
d'échéance sur les options. Les options d'achat, aussi bien que
les options de vente, voient leur valeur s'accroitre (ou au moins ne pas
baisser) lorsque la date de maturité s'éloigne, c'est à
dire quand la durée restant à courir jus-qu'à
l'échéance augmente. Considérons deux options qui
diffèrent seulement par la date d'échéance. Le
propriétaire de l'option à durée de vie plus longue
profite de toutes les opportunités d'exercice ouvertes ouvertes au
propriétaires des options à durée de vie plus
10
FIGURE 1.1 - Impact des variations du taux de change, du prix
d'exercice et de durée de vie jusqu'à l'échéance
sur la valeur d'une option lorsque S0 = 50, K = 50, r
= 5%, ó = 30% et T = 1, [14].
courte, et plus encore. La valeur de l'option à
l'échéance plus longue est toujours supérieur à
celle de l'option à l'échéance plus courte. Les graphiques
e, f de la figure 1.1 illustrent de quelle manière la valeur des options
d'achat et de vente dépend de la date d'échéance.
Volatilité du taux de change
La volatilité du taux de change mesure l'incertitude
quant aux variations futures de ce taux. Plus la volatilité est grande,
plus la probabilité que le taux de change atteigne des sommets, ou
subisse de fortes baisses, est importante. Le détenteur d'un call
bénéficie d'une hausse du taux de change, mais limite son risque
de perte, puisqu'en cas de chute du taux de change, il ne subit qu'une perte
liée à la valeur de son option. Réciproquement, le
détenteur d'un put bénéficie de la baisse du taux de
change, mais il limite également son risque en cas de hausse du taux.
Par conséquent, la valeur des calls, comme celle des puts, augmente avec
la volatilité du sous-jacent (voir graphiques a et b de la figure
1.2).
11
Taux d'intérêt sans risque
Le taux d'intérêt sans risque affecte la valeur
de l'option d'une façon moins évidente. Lorsque les taux
d'intérêt augmentent, l'espérance de rendement, attendu par
les investisseurs, tend à s'élever également. Mais la
valeur actuelle des flux de trésorerie futurs reçus par les
détenteurs d'options diminue. L'impact combiné de ces deux effets
entraîne une baisse de la valeur des options de vente et un accroissement
de la valeur des options d'achat (voir graphiques c et d de la figure 1.2).
Il est important de souligner que nous envisageons ici une
variation des taux d'intérêt tandis que toutes les autres
variables demeurent inchangées.
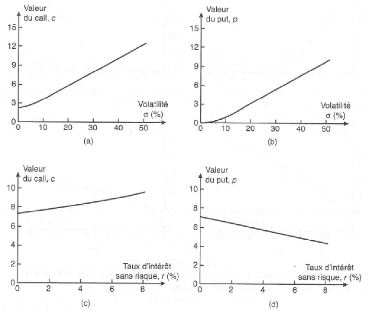
FIGURE 1.2 - Impact des variations de la volatilité et
taux d'intérêt sans risque sur la valeur d'une option lorsque
S0 = 50, K = 50, r = 5%, ó = 30%
et T = 1, [14].
12
| 


