6.2 Modélisation du taux de change marocain dans
le cadre d'un régime de change flottant administré
Un régime de flottement administré est un
système de taux de change convenu dans lequel certains pays, le Maroc
faisant partie, s'engagent à maintenir leur taux de change dans une
marge ou une bande de fluctuation spécifique. Cette marge peut
être fixée par rapport à une autre devise ou à un
panier de devises. L'amplitude de cette bande peut toutefois varier, donnant
lieu à deux versions différentes:
-- Version forte : Également connue sous le nom
Fixed Peg Arrangement. Le taux de change, qui fluctue dans des marges
de #177;1% ou moins, est révisé assez rarement. L'autorité
monétaire peut maintenir le taux de change dans les marges par une
intervention directe (par exemple, en achetant et en vendant des devises
domestiques et étrangères sur le marché) ou indirecte (par
exemple, en influant sur les taux d'intérêt).
77
-- Version faible : Également connue
sous le nom de Target Zone Exchange Rate. Dans ce cas, le taux de
change fluctue de plus de #177;1% autour d'un cours de référence
publié par la banque centrale. Une fois que le taux de change atteint
une des deux extrémités, les autorités interviennent sur
le marché de change en rachetant ou vendant un montant de devises
suffisant pour maintenir le taux de change à l'intérieur de la
bande.
La modélisation des taux de change sous un
régime de flottement administré, est une tentative pour expliquer
formellement comment le taux de change se comporte à l'intérieur
de la bande de fluctuation. Il existe une vaste littérature sur les
Target Zones, théorique et empirique. La littérature
théorique moderne a son point de départ dans le modèle de
la Target Zone de Krugman (1991) [20] qui sera décrit
ci-dessous. Le modèle a ensuite été modifié pour
les situations dans lesquelles son hypothèse de base, selon laquelle les
interventions de la banque centrale ne se produisent qu'aux frontières
de la bande de fluctuation, n'est pas satisfaite. Citons par exemple
Delgado et Dumas (1992) [10] et Torres (2000) [30]. Le
modèle Krugman a été testé de différentes
manières dans de nombreuses contributions empiriques, et une observation
générale est qu'il n'a pas réussi à
caractériser les mouvements des taux de change à
l'intérieur d'une bande de fluctuation, Target Zone.
Le modèle Krugman est un modèle
à temps continu, et il y a eu de nombreuses tentatives de l'ajuster
à diverses séries de taux de change quotidiens en utilisant la
méthode des moments : voir par exemple Smith et Spencer (1992)
[26], De Jong (1994) [18], Iannizzotto et Taylor (1999)
[16] et Taylor et Iannizzotto (2001) [17]. Une autre approche,
à temps discret, Bekaert et Gray (1998) [3], a
été de modéliser la distribution conditionnelle de la dans
une zone de fluctuation en supposant que la distribution est normale
tronquée, la troncature étant le résultat de l'existence
d'une zone crédible.
Dans ce chapitre, nous reprenons les travaux de Lundbergh
et Teräsvirta (2005), où ils proposent un modèle
à temps discret qu'il l'ont appelé Smooth Transition
Autoregressive Target Zone (STARTZ). Leur objectif a été de
développer un modèle qui permettra à la fois d'exa-miner
la validité des hypothèses du modèle de Krugman
et, en même temps, de caractériser adéquatement le
comportement dynamique d'un taux de change fluctuant à
l'intérieur d'une bande de fluctuation.
Le plan de ce chapitre est comme suit : Le modèle
classique de Krugman est discuté dans la Section 1, le
modèle STARTZ est défini dans la Section 2, la Section 3
est consacrée méthodologie d'estimation du modèle, la
Section 4 à l'application et l'évaluation du modèle sur le
taux de change marocain. Finalement, la Section 5 conclut.
6.2.1 Le modèle de Krugman
Krugman considère un modèle
monétaire log-linéaire minimaliste du taux de change. Exprimant
toutes les variables en logarithmes, le taux de change à tout chaque
instant t est supposé égal à :
s(t) = f(t) + áE(ds
dt |Ft) (6.1)
avec s(t) est le logarithme du taux de change spot
à l'instant t, mesuré en unités de devise
domestique par unité de devise étrangère ou un panier de
devises étrangères. f(t) est ce qu'on appelle le
fondamental et E(ds
dt |Ft) est l'espérance
conditionnelle de la variation du taux de change à l'instant t
sachant la filtration Ft, qui représente l'information
dispo-
78
nible à cet instant, celle-ci inclut la valeur actuelle du
fondamental f(t), ainsi que toutes les restrictions explicites ou
implicites que les autorités ont imposées à
l'évolution future du fondamental.
Le fondamental f(t) peut s'écrire comme suit:
f(t) = m(t) + v(t) (6.2)
avec m(t) représente la masse monétaire
à l'instant t, c'est un paramètre contrôlé
par la banque centrale. v(t) contient tous les autres facteurs qui
influent sur le taux de change. On suppose que cette composante suit un
mouvement Brownien.
dv = ódz
avec z est un processus de Wiener standard.
La composante m(t) n'est modifié que pour
maintenir le taux de change à l'intérieur de la bande. Plus
précisément, l'autorité monétaire est prête
à réduire m afin d'empêcher s de
dépasser une certaine valeur maximale sU, et
à augmenter m pour empêcher s de tomber en
dessous d'une certaine valeur minimale sL. Tant que
sL < s < sU, la composante m(t)
reste inchangée.
S'il n'y a pas de bande de fluctuation et que la monnaie
flotte librement, la banque centrale n'intervient pas (m =
0), et f, et donc s, suit un mouvement
Brownien. Dans ce cas E(ds dt |Ft) = 0.
Il n'y a aucune raison économique de supposer une
mouvement Brownien sur v. L'hypo-thèse est faite ici pour deux
raisons:
-- L'hypothèse d'une marche aléatoire permet de
ce concentrer entièrement sur la dynamique causée par la
présence d'une bande de fluctuation.
-- L'hypothèse de marche aléatoire donne lieu
à une solution analytique simple.
Avant de passer à la solution analytique, il est utile
de commencer par une approche intuitive des effets d'une bande de fluctuation
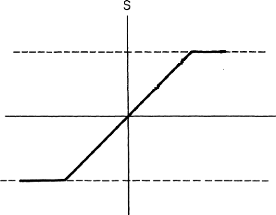
sur le comportement des taux de change. La figure 6.1 représente le taux
de change par rapport à v; la bande de fluctuation est
indiquée par les lignes en pointillés qui définissent une
bande qui limite le taux de change entre sL et
sU. Nous considérons le comportement du taux de
change lorsque l'on part d'une certaine masse monétaire initiale, disons
m = 0.
Une vision naïve se présenterait comme suit:
Puisque m est détenu localement constante et puisque v
suit un mouvement Brownien, alors E(ds dt |Ft) =
0. Ainsi, on pourrait simplement s'attendre à ce que le taux de
change soit égal à m + v, c'est-à-dire que le
taux de change flotte librement l'intérieur de la bande de fluctuation.
Si les chocs successifs à v poussent le taux de change aux
bords de la bande de fluctuation, alors la masse monétaire m
sera ajustée pour éviter que s ne dérive
davantage. Ainsi, cette vision naïve supposerait une relation entre v
et s qui ressemble à la ligne épaisse de la figure
6.1.
79
FIGURE 6.1 - Représentation de s en fonction
de v, [20].
Krugman suppose l'existence d'une bande de
fluctuation, sL = s = sU, et
que les autorités interviennent à travers le paramètre
m quand le taux de change atteint l'une des deux frontières
sL ou sU. Cela change les anticipations
des agents lorsque la zone est crédible. Lorsque le taux de change se
trouve près de l'une des deux frontières, la probabilité
que le taux de change se déplace vers le centre est perçue comme
étant plus élevée que la probabilité qu'il se
rapproche encore de la frontière. Les agents anticipent l'intervention,
E(ds
dt |Ft) =6 0, de sorte que la zone
crée une non-linéarité appelée Honeymoon Effect
dans le comportement du taux de change en fonction du fondamental. Au lieu
d'une ligne droite, la relation entre le taux de change et fondamentale est
caractérisée par une courbe en S lisse représentée
dans la figure 6.2.
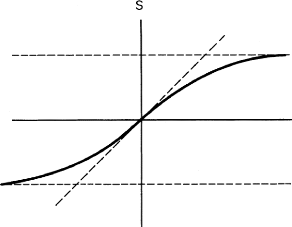
FIGURE 6.2 - Représentation de s en fonction de
v, [20].
80
Nous voulons déterminer une relation,
s = g(m, v, sL,
sU) (6.3)
qui est cohérente avec l'équation du modèle
(6.1), et le comportement du taux de change supposé.
Supposons que nous maintenions m constant,
c'est-à-dire que nous considérons une situation où s
se situe à l'intérieur de la bande. Alors la seule source de
changements espérés dans s réside dans le
mouvement aléatoire de v. On a donc :
E(ds
dt|Ft) = ó22
gvv(m, v, sL,
sU) (6.4)
avec
g
gvv(m, v, sL, sU
a2 ) = av2
En substituant (6.4) dans (6.1), nous aurons :
g(m, v, sL,
sU) = m + v + acr22 gvv(m, v,
sL, sU) (6.5)
La solution générale de l'équation (6.5) est
de la forme :
g(m, v, sL,
sU) = m + v + AeP(m+v) + Be-P(m+v) (6.6)
avec
_ /2a2 P a
et A et B sont des constantes à
déterminer à l'aide des conditions aux limites satisfaites par le
taux de change s au moment de l'intervention.
Nous pouvons encore simplifier le problème en invoquant
la symétrie. Supposons que m = 0; alors nous nous attendons
sûrement à ce que la relation passe par le milieu de la figure
6.2, c'est-à-dire que s = 0 lorsque v = 0. Cela ne
peut être vrai que si B = -A. L'équation (6.6) peut donc
s'écrire :
g(m, v, sL,
sU) = m + v + A(eP(m+v) - e-P(m+v)) (6.7)
| 


