5.2 Stratégies dynamiques de couverture
Notre discussion jusqu'à présent devrait
permettre de comprendre pourquoi les traders utilisent des modèles
théoriques pour évaluer les options. Tout d'abord, un
modèle nous renseigne sur la valeur d'une option. Nous pouvons comparer
cette valeur avec le prix de l'op-tion sur le marché et, à partir
de là, choisir une stratégie appropriée.
Deuxièmement, une fois que nous avons pris position, le modèle
nous aide à quantifier un grand nombre des risques que comporte la
négociation de l'option. En comprenant ces risques, nous serons mieux
préparés à minimiser nos pertes lorsque les conditions du
marché jouent contre nous et à maximiser nos profits lorsque les
conditions du marché jouent en notre faveur, c'est ce qu'on appelle la
couverture dynamique.
La couverture dynamique se différencie des
stratégies de couverture statiques, vues dans la section
précédente, dans lesquelles la couverture est définie
dès le départ et n'est plus jamais ajustée. La couverture
dynamique est réalisée par le biais des lettre grecques, vues
plus haut dans ce rapport, telles que le delta, le gamma et le vega. Ces
mesures quantifient les différents aspects du risque dans une position
en options.
60
5.2.1 Delta Hedging
Le delta d'une option, noté , a été
introduit plus haut dans le chapitre 2. C'est le taux de variation de la valeur
de l'option par rapport à celle du sous-jacent. C'est aussi la pente de
la courbe reliant la valeur de l'option à celle du sous-jacent (voir
figure 2.2). Le delta d'un call est donné par:
ac
= aS
où c est la valeur du call et S le cours
de l'action. Le delta d'un portefeuille d'options est:
aLI
aS
où LI représente la valeur du portefeuille.
Le delta du portefeuille peut être calculé
à partir des deltas de chacune des options du portefeuille prises
individuellement du fait de la linéarité du passage aux
dérivées partielles.
Si un portefeuille est constitué d'une quantité
wi d'une option i (1 i n), le delta
du
portefeuille est obtenu par:
|
où i représente le delta de
l'option i.
|
=
|
n
?
i=1
|
wi i
|
Le delta est étroitement lié au modèle de
Black-Scholes, ils ont montré qu'il était possible
d'établir un portefeuille sans risque consistant sur une position sur le
sous-jacent, et une position sur l'option. Le portefeuille de Black-Scholes est
constitué par:
-- La vente d'une option.
-- L'achat d'une quantité du sous jacent.
Une position dont de delta est nul est appelée position
delta-neutre. Il est important de comprendre que, puisque le delta varie, la
position de l'investisseur reste couverte en delta-neutre seulement dans un
intervalle de temps relativement court. La couverture doit être
réajustée périodiquement, d'où l'appellation de
couverture dynamique.
Exemple
Pour illustrer plus clairement cet aspect dynamique de la
couverture, nous allons travailler sur un exemple dans lequel un call
Européen sur EURUSD est vendu. La couverture est sensée
être ajustée chaque semaine jusqu'à
l'échéance de l'option. Les inputs du call sont:
-- Notionnel: 100000
-- Spot : 1,1177
-- Strike : 1,08
-- Maturité : 20 semaines
-- Taux domestique : 1,679%
-- Taux étranger: -0,398%
-- Volatilite : 5,0492% (Donnée par le
modèle de Vanna-Volga)
Nous Avons donc d'après le modèle de
Garman-Kohlhagen :
Prix de l'option : 4 773,41
Delta : 0, 701
Le tableau ci-dessous présente les différentes
opérations de couverture pendant la durée de vie de l'option :
TABLE 5.8 - Simulation de la couverture dynamique par delta.
|
Sem
|
Taux
EURUSD
|
Delta
|
Emprunt
USD
|
Placement EUR
|
P&L
Intérêt
|
P&L
Devise
|
P&L
Option
|
P&L
Total
|
|
0
|
1,1177
|
0, 701
|
73 590, 83
|
70112, 05
|
-
|
-
|
-
|
-
|
|
1
|
1,1160
|
0, 689
|
72 208, 48
|
68 873, 39
|
-29, 76
|
-119,19
|
209, 25
|
60, 31
|
|
2
|
1,1122
|
0, 668
|
69 944, 93
|
66 838,18
|
-29, 23
|
-261, 72
|
398, 70
|
107, 76
|
|
3
|
1,1090
|
0, 650
|
67957, 05
|
65 045, 68
|
-28, 33
|
-213, 88
|
341, 28
|
99, 07
|
|
4
|
1,1025
|
0, 620
|
64 620, 06
|
62 018, 93
|
-27, 55
|
-422, 80
|
619, 40
|
169, 05
|
|
5
|
1,1094
|
0, 641
|
66 874, 04
|
64 050, 65
|
-26, 20
|
427, 93
|
-539, 78
|
-138, 06
|
|
6
|
1, 0945
|
0, 580
|
60 289, 94
|
58 035, 03
|
-27,17
|
-954, 35
|
1313,10
|
331, 57
|
|
7
|
1, 0832
|
0, 535
|
55 335, 71
|
53 461, 33
|
-24, 48
|
-655, 80
|
867, 34
|
187, 07
|
|
8
|
1, 0845
|
0, 536
|
55 537, 32
|
53 647, 23
|
-22, 46
|
69, 50
|
-10, 84
|
36, 21
|
|
9
|
1,1026
|
0, 595
|
61972, 96
|
59 484, 01
|
-22, 57
|
971, 01
|
-1325, 21
|
-376, 76
|
|
10
|
1,1286
|
0, 669
|
70 343, 68
|
66 900, 92
|
-25, 26
|
1546, 58
|
-2 407, 73
|
-886, 41
|
|
11
|
1,1106
|
0, 608
|
63 608, 55
|
60 836, 51
|
-28, 79
|
-1204, 22
|
1800, 66
|
567, 65
|
|
12
|
1, 0695
|
0, 480
|
49 849, 98
|
47 972, 02
|
-26, 00
|
-2 500, 38
|
3 000, 32
|
473, 93
|
|
13
|
1,1142
|
0, 602
|
63 496, 20
|
60 219, 57
|
-20, 26
|
2144, 35
|
-3 240, 98
|
-1116, 89
|
|
14
|
1, 0809
|
0, 510
|
53 496, 46
|
50 968, 27
|
-25, 98
|
-2 005, 31
|
2 847,11
|
815, 81
|
|
15
|
1, 0936
|
0, 537
|
56 506, 65
|
53 720, 82
|
-21, 79
|
647, 30
|
-825, 64
|
-200,14
|
|
16
|
1, 0878
|
0, 520
|
54 654, 02
|
52 017, 72
|
-23, 09
|
-311, 58
|
540, 90
|
206, 23
|
|
17
|
1, 0821
|
0, 506
|
53149, 56
|
50 627, 41
|
-22, 34
|
-296, 50
|
477, 08
|
158, 24
|
|
18
|
1, 0985
|
0, 527
|
55 448,17
|
52 719, 90
|
-21, 72
|
830, 29
|
-1246, 69
|
-438,13
|
|
19
|
1, 0841
|
0, 505
|
53 008, 73
|
50 469, 71
|
-22, 75
|
-759, 17
|
1375, 63
|
593, 71
|
|
20
|
1, 0815
|
1, 000
|
106 575, 74
|
100 000, 00
|
-21, 71
|
-131, 22
|
429, 52
|
276, 59
|
Le graphe du Profit & Loss est
représenté dans la figure ci-dessous :
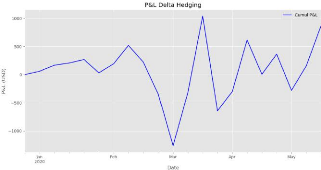
FIGURE 5.4 - Profit & Loss Delta Hedging.
61
62
Pour bien expliquer d'où proviennent les coûts,
nous allons détailler les opération effectuées pour les
deux premières semaines, on suit la même démarche pour les
semaines qui suivent:
Semaine 0
-- Taux de change EURUSD : 1,1177.
-- Prix de l'option : 4773,41 USD.
-- Delta : 0,701 ce qui est équivalent
à 70112,05 EUR, et 78364,24 USD.
Pour couvrir cette position, le trader doit acheter la
quantité delta en EUR qui est 70112,05 EUR. Pour réaliser cette
opération il doit:
-- Emprunter 73590,83 USD (78 364,24 USD -4773,41 USD) à
un taux de 1,679%. -- Placer 70112,05 EUR à un taux de -0,398%.
Semaine 1
-- Taux de change EURUSD : 1,1160.
-- Prix de l'option : 4564,15 USD.
-- Delta : 0,689 ce qui est équivalent
à 68873,39 EUR, et 76862,70 USD.
La différence entre le delta de la semaine 0 et le delta
de la semaine 1 est:
ÄS1 - ÄS0 = -0,012
Pour couvrir cette position, le trader doit vendre
l'équivalent de la différence de delta qui est 1238,657 EUR. Les
nouvelle valeurs de placement et emprunt seront donc:
-- Placement: 68873,39 EUR. --
Emprunt: 72208,4857 USD.
Le Profit & Loss total de l'opération de
couverture entre les deux semaines se divise en trois parties:
-- P&L Option : Se calcule de la
manière suivante:
P&L OptionS1 = Prix de
l0optionS0 - Prix de
l0optionS1 Dans notre cas on a : P&L
OptionS1 = 209,25 USD.
-- P&L Sous-jacent: Se calcule de la
manière suivante:
P&L Sous jacentS1 = ÄS0
× Notionnel × (Taux de changeS1 - Taux de
changeS0) Dans notre cas on a : P&L Sous -
jacentS1 = -119,19 USD.
-- P&L Intérêts : Se calcule de
la manière suivante:
P&L Int'eràetsS1 =
EmpruntS0 × (1 - erd/52) - Taux de changeS0
× PlacementS0 × (1 - erf
/52) Dans notre cas on a : P&L
Int'eràetsS1 = -29,76 USD.
63
Application
Le même raisonnement présenté dans
l'exemple précédent peut être appliqué sur un
portefeuille contenant plusieurs options. Nous avons développé un
outil qui permet la gestion dynamique d'un portefeuille d'options
Européennes sur devises, en prenant en compte tous les facteurs
dynamiques entrant dans la gestion des options à savoir : Les taux
d'intérêt, le taux de change et la surface de volatilité.
Cet outil est composé des éléments suivants:
-- Une interface qui permet l'ajout ou la suppression d'une
option de la base de données. -- Une base de données qui contient
les différentes options qui constituent le portefeuille.
-- Une composante qui donne le Mark-To-Market du
portefeuille.
-- Une feuille Excel qui permet de faire l'ajustement
quotidien du portefeuille, et permet aussi de calculer le Profit & Loss
journalier.
Interface d'ajout/suppression
Cette interface ce compose de deux fenêtres : "Interface de
saisie" et "Portefeuille".
La première fenêtre, représentée
dans la figure 5.5, permet de remplir tous les champs requis afin d'ajouter
l'option à la base de données, puis en cliquant sur "Ajouter"
l'option sera enregistrée dans le portefeuille, cette interface permet
aussi d'afficher le prix et les sensibilités de l'option
ajoutée.
La deuxième fenêtre, représentée
dans la figure 5.6, est un aperçu du portefeuille, elle contient toute
les informations des options existante, elle sert aussi à supprimer une
option du portefeuille en la sélectionnant et en cliquant dur
"Supprimer".
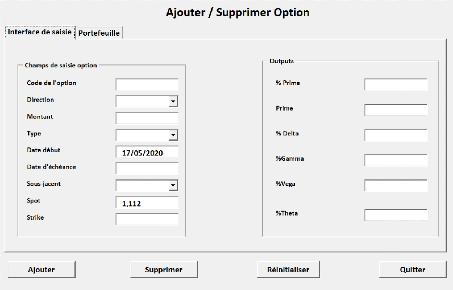
FIGURE 5.5 - Aperçu de l'interface de saisie.
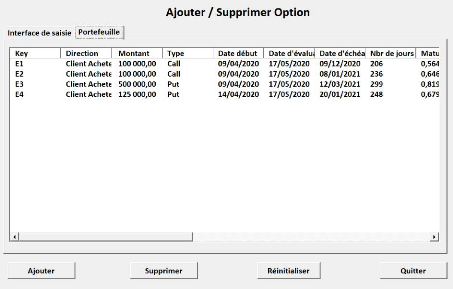
64
FIGURE 5.6 - Aperçu du portefeuille d'options.
Base de données
Notre base de données est une feuille Excel,
représentée dans la figure 5.7, qui contient toutes les
options du portefeuille, après avoir rempli les champs dans l'interface
d'ajout/suppression et cliquer sur "Ajouter", l'option s'ajoute automatiquement
sur la feuille Excel, cette feuille contient aussi les prix de chaque
option et ses sensibilités au jour le jour.

FIGURE 5.7 - Extrait de la base de données des
options.
Mark-To-Market
La composante qui donne le Mark-To-Market du
portefeuille, représentée dans la figure 5.8, permet de donner la
valeur et les sensibilités du portefeuille au jour le jour. Elle
contient aussi un bouton "Ajuster le portefeuille" qui permet de faire les
calculs présentées dans l'exemple précédent, en
ajoutant une ligne qui correspond à la date du jour dans la feuille
d'ajustement.
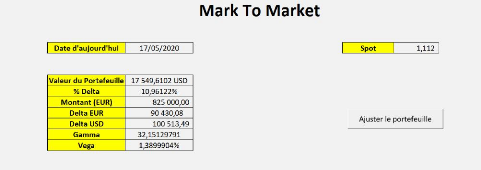
65
FIGURE 5.8 - Interface Mark-To-Market du
portefeuille.
Feuille d'ajustement
La feuille d'ajustement, représentée dans la
figure 5.9, contient les mêmes informations présentées dans
l'exemple précédent, elle sert à ajuster le portefeuille
quotidiennement afin de se couvrir par le delta. Elle permet aussi le suivi du
Profit & Loss quotidien depuis la date d'ouverture de la
première option jusqu'à la date au jour le jour.
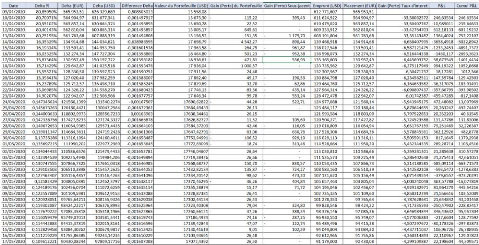
FIGURE 5.9 - Extrait de la feuille d'ajustement.
La figure 5.10 représente le graphe du Profit &
Loss cumulé de la stratégie depuis la date d'ouverture de la
première option jusqu'à la date au jour le jour.
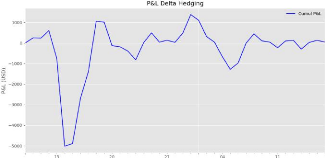
66
FIGURE 5.10 - Profit & Loss du portefeuille.
|
|



