Le marché de change marocain. évaluation et couverture des options européennes et américaines de change et modélisation du taux de change du dirham.

5.1.2 Risk Reversal

Une stratégie Risk Reversal consiste à acheter/vendre un call en dehors de la monnaie et vendre/acheter un put en dehors de la monnaie, les deux ayant la même date d'échéance.

Dans cette stratégie, l'investisseur fait d'abord une intuition du marché; si cette intuition est haussière, il voudra être long. Cependant, au lieu d'être long sur le sous-jacent, il achètera un call hors de la monnaie de strike K2 et vendra simultanément un put hors de la monnaie de strike K1 avec K1 < K2. Si son intuition est baissière, il vaudra être court sur Risk Reversal en achetant un put hors de la monnaie de strike K1, et en vendant un call hors de la monnaie de strike K2.

TABLE 5.3 - Revenus d'une position longue sur Risk Reversal.

Taux de change	Payoff achat du call	Payoff vente du put	Payoff total
ST = K2	ST - K2	0	ST - K2
K1 < ST < K2	0	0	0
ST = K1	0	ST - K1	ST - K1

TABLE 5.4 - Revenus d'une position courte sur Risk Reversal.

Taux de change	Payoff vente du call	Payoff achat du put	Payoff total
ST = K2	K2 - ST	0	K2 - ST
K1 < ST < K2	0	0	0
ST = K1	0	K1 - ST	K1 - ST

Pour que cette stratégie soit zero-cost il faut trouver les deux strikes _K01 ^et _K02 du put et du call respectivement, qui permettent d'annuler la prime de la stratégie Risk Reversal. Pour cela if faut résoudre l'équation suivante:

p(K01) - c(K02) = 0 (5.1)

L'équation (5.1) peut être résolue numériquement en utilisant l'algorithme de Newton-Raphson d'écrit plus haut.

Nous avons d'après le modèle de Garman-Kohlhagen :

c(K) = S0e^-rf ^TN(d1) - Ke^-rdTN(d2)
p(K) = Ke^-rdTN(-d2) - S0e^-rf ^TN(-d1)

avec :	d1(K) =	ln(S0/K) + (rd - rf + cr^2/2)T
et :		v cr T

d2(K) = v

cr T

ln(S0/K) + (rd - rf - cr²/2)T

v

= d1(K) - cr T

On initialise l'algorithme en choisissant :

K01 = S0 et K02 = S0

Pour chaque itération de l'algorithme de Newton-Raphson, on calcule Kn+1

01 et Kn+1

02 à partir

de Kⁿ₀₁ et _Kn02, tels que :

Kn+1 = Kn

01 01 p0(Kn01)

p(Kⁿ₀₁) - c(Kⁿ₀₁)

et

02)

_Kn+1

02 = Kn 02 + p(Kn ₀₂) - c(Kⁿ c⁰(Kⁿ₀₁)

Avec :

c⁰(K) = S0e^-rf ^Td⁰₁(K)N⁰(d1) - e^-rd^T(N(d2) + Kd⁰₂(K)N⁰(d2) (5.2)

et

p⁰(K) = S0e^-rf ^Td⁰₁(K)N⁰(-d1) + e^-rdT(N(-d2) - Kd⁰2(K)N⁰(-d2)) (5.3)

où :

d⁰₁(K) = d⁰2(K) = -cr1

KvT

Ci-dessous l'algorithme de Newton-Raphson pour trouver les deux strikes _K01 ^et K02 :

Algorithm 2: Algorithme de Newton-Raphson pour _K01 ^et K02.

K01 ? S0

K02 ? S0 e ? 10-⁸

while |p(K01) - c(K02)| = e do

K01 ?K01 - p(K01)-c(K02)

p⁰(K01)

while |p(K01) - c(K02)| = e do

K02 ?K02 + p(K01)-c(K02)

c⁰(K02)

end

end

return K01, K02

54

55

5.1.3 Butterfly spread

Un Butterfly Spread implique des positions sur des options de trois prix d'exercice différents. Il peut être créé en achetant un call au prix d'exercice bas K1, en achetant un call au prix d'exercice plus élevé K3 et en vendant deux calls de prix d'exercice K2, situé entre K1 et K3.

Généralement, K2 est proche du prix spot du sous-jacent. Le profil de gain de cette stratégie est représenté dans la figure 5.2.

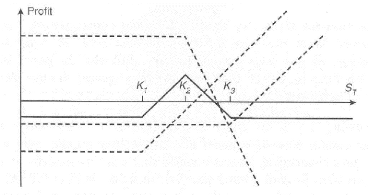
FIGURE 5.2 - Payoff d'un Butterfly Spread.

Un Butterfly Spread produit un bénéfice si le cours de l'action reste proche de K2, mais conduit à de faibles pertes si le cours du sous-jacent varie de façon significative à la hausse comme à la baisse. C'est, par conséquent, une stratégie judicieuse pour un investisseur qui pense qu'une variation importante du cours est improbable.

TABLE 5.5 - Revenus d'une position longue sur Butterfly Spread.

Taux de change	Payoff achat du premier call	Payoff achat du second call	Payoff vente des deux calls	Payoff total
ST < K1	0	0	0	0
K1 < ST < K2	ST - K1	0	0	ST - K1
K2 < ST < K3	ST - K1	0	-2(ST - K2)	K3 - ST
ST > K3	ST - K1	ST - K3	-2(ST - K2)	0

Ces revenus sont calculés en considérant K2 = 0, 5(K1 + K3)

Pour que cette stratégie soit zero-cost il faut trouver les trois strikes K01, K02 ^et _K03 des calls qui constituent cette stratégie, et qui permettent d'annuler la prime de la stratégie Butterfly Spread. Pour cela if faut résoudre l'équation suivante :

2c(K02) - c(K01) - c(K03) = 0 (5.4)

De la même manière que la stratégie précédente, nous allons résoudre l'équation (5.4) numériquement en utilisant l'algorithme de Newton-Raphson.

56

On fixe K02 = S0, et on initialise l'algorithme en choisissant:

K01 = S0 - 0,01 et K02 = S0 + 0,01

Pour chaque itération de l'algorithme de Newton-Raphson, on calcule Kn+1

01 et Kn+1

03 à partir

de Kn 01 et _Kn03, tels que:

03)

_Kn+1

01 = Kn 01 + 2c(Kn ₀₂) - c(Kn ₀₁) - c(Kⁿ

c⁰(Kⁿ₀₁)

et

03)

_Kn+1

03 = Kn 03 + 2c(Kn ₀₂) - c(Kn ₀₁) - c(Kⁿ

c⁰(Kⁿ₀₃)

Avec c⁰(K) définie dans l'équation (5.2).

Ci-dessous l'algorithme de Newton-Raphson pour trouver les trois strikes K01, K02 ^et K03 :

Algorithm 3: Algorithme de Newton-Raphson pour K01, K02 ^et K03.

K01 ? S0 - 0,01

K02 ? S0

K03 ? S0 + 0,01

e ? 10-⁸

while |2c(K02) - c(K01) - c(K03)| = e do

K01 ? K01 + 2c(K02)-c(K01)-c(K03)

c⁰(K01)

while |2c(K02) - c(K01) - c(K03)| = e do

K03 ? K03 + 2c(K02)-c(K01)-c(K03)

c⁰(K03)

end

end

return K01, K02, K03