3.3 Application
Après avoir présenté les notions
théoriques derrière la méthode de Vanna-Volga, nous allons
maintenant les appliquer pour développer un outil qui permet de calculer
la volatilité implicite de l'EURUSD pour un strike K et une
maturité T données.
L'outil à été développé sous
Python, il a été ensuite utilisé comme
étant une fonction Excel à l'aide d'un outil qui permet
de relier les deux plateformes.
Les inputs de cette outil sont le strike K et la
maturité T, il permet ensuite de faire une interpolation
bilinéaire par rapport à ces deux variables.
Comme nous avons mentionné dans la section
précédente, les cotations utilisés pour la méthodes
de Vanna-Volga sont : crATM, crRR et
crBF. Les données de ces trois cotations sont
représentées dans la figure 3.4, pour des maturités allant
jusqu'à 10 ans.
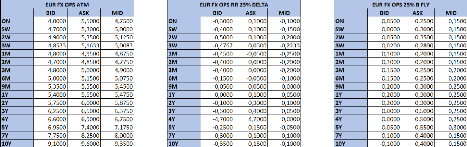
32
FIGURE 3.4 - Données du marché pour les 3
volatilités crATM, crRR et
crBF.
En plus du smile de volatilité, les traders
tiennent compte de la structure par termes des volatilités lorsqu'ils
évaluent des options. Concrètement, la volatilité
utilisée pour évaluer une option à la monnaie
dépend de la durée de vie de cette option. Elle tend à
être une fonction croissante de la maturité lorsque les
volatilités historiques à court terme sont faibles. Cela traduit
le fait que les opérateurs anticipent une hausse de la
volatilité. Symétriquement, la
volatilité tend à être une fonction
décroissante de la maturité lorsque les volatilités
historiques à court terme sont élevées. Cela traduit
également l'anticipation d'une baisse future de la volatilité.
Une surface de volatilité combine les smiles
de volatilité et la structure par termes des volatilités, elle
est souvent présentée sous la forme d'un tableau donnant les
volatilités implicites en fonction du prix d'exercice et de la
durée de vie. Un exemple de surface de volatilité pour l'EURUSD
est représentée dans la figure 3.5.
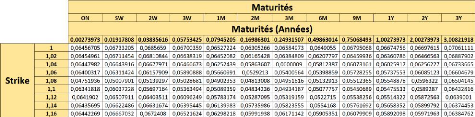
FIGURE 3.5 - Matrice de volatilité pour l'EURUSD.
Une des dimensions de ce tableau est le prix d'exercice,
l'autre la durée de vie résiduelle de l'option. Les
éléments du tableau donnent les différentes valeurs de
volatilité implicite calculées par la méthode de
Vanna-Volga. Pour chaque maturité, certaines données
correspondent à des options liquides pour lesquelles les prix de
marché sont fiables. Les autres éléments du tableau sont
calculés par interpolation linéaire.
La surface de volatilité qui correspond à ce
tableau est représentée dans la figure 3.6.
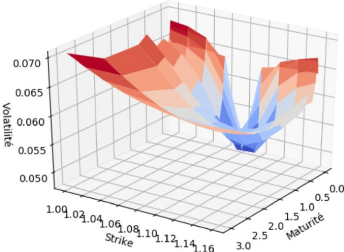
FIGURE 3.6 - Surface de volatilité pour l'EURUSD.
33
34
Les smiles de volatilité correspondant à
chaque maturité sont représentés dans la figure 3.7.
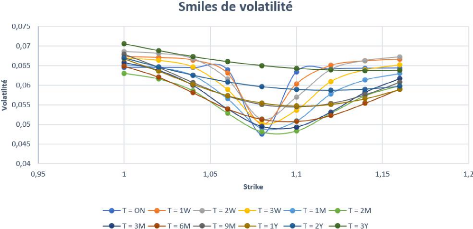
FIGURE 3.7 - Smiles de volatilité pour
l'EURUSD.
On peut dire que l'impact, sur les options, des variations
extrêmes et de l'instabilité de la volatilité du
sous-jacent dépend de l'échéance des options. L'impact
relatif de l'instabilité de la volatilité sur les cours des
options croît avec la durée de vie de l'option, mais le Smile
de volatilité créé par l'instabilité de la
volatilité devient généralement moins prononcé.
35
| 


