27
3.2 Estimation de la volatilité implicite
La volatilité implicite est calculée à
partir des prix de marché des produits les plus liquides et de la
formule théorique d'évaluation d'option. Elle est obtenue en
inversant la formule de Black-Scholes qui donne le prix cBS
du call par rapport au prix cobs du call
observé sur le marché, à un niveau de cours actuel
donné, pour une maturité et un strike donné. Cette
volatilité implicite crimp est donc donnée par la
relation:
cBS(K, T, crimp) =
cobs(K, T)
C'est donc un problème dit inverse et qui
définit bien de manière unique crimp puisque le prix
cBS de Black-Scholes est une fonction strictement
croissante de la volatilité.
Il n'y a pas de formule explicite pour crimp et on a
recours à des méthodes numériques pour la calculer :
Méthode de Newton Raphson, méthodes par
dichotomie, méthode de splines cubiques, modèle de
Vanna-Volga.
Notons que crimp dépend du strike et de la
maturité liés au prix du call observé. Souvent, on calcule
cette volatilité implicite pour différents strikes et/ou
différentes maturités de call et on représente alors son
graphe en fonction du strike et/ou de la maturité.
Dans cette section nous allons présenter
brièvement la méthode de Newton-Raphson, puis nous
allons se concentrer sur le modèle de Vanna-Volga car il est le plus
adapté pour le marché de change.
3.2.1 Méthode de Newton-Raphson
L'algorithme de Newton-Raphson est utilisé pour
trouver une approximation de la solution d'une fonction f(x)
= 0. Le principe étant de partir d'une valeur initiale et d'approximer
le résultat espéré à l'aide de la tangente en ce
point. En effet, une tangente T étant affine, il est facile de
trouver une solution x telle que T(x) = 0. Ainsi on
peut définir la récurrence
suivante:
f(xn)
xn+1 = xn - f
0(xn)
La figure 3.3 représente le principe de cette
méthode:
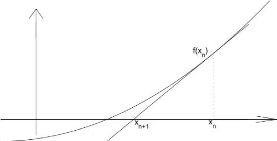
FIGURE 3.3 - Principe de le méthode de
Newton-Raphson.
Afin de calculer la volatilité implicite à l'aide
de la méthode de Newton-Raphson, on cherchera donc à minimiser la
fonction suivante:
f(wimp) = cBS(K, T, wimp) -
cobs(K, T)
A chaque itération il faut calculer wn+1
à partir du wn obtenu dans l'itération
précédente, tel que:
wn+1 = wn
cBS(K, T, wn) -
cobs(K, T)
c0 BS(K, T,
wn)
Or, dériver cBS(K, T, wimp) -
cobs(K, T) par rapport à wimp revient
à calculer le Vega défini dans le chapitre
précédent, on peut donc réécrire l'équation
sous la forme:
wn+1 = wn
|
cBS(K, T, wn) -
cobs(K, T)
|
|
|
Ci-dessous l'algorithme de Newton-Raphson:
Algorithm 1: Algorithme de Newton-Raphson.
wimp ? w0 e ? 10-4
while cBS(K, T, wimp)
- cobs(K, T) = e do
wimp ? wimp
cBS(K,T,wimp)-cobs(K,T)
c0 BS(K,T,wimp)
end
return wimp
| 


