3.1.2 Volatilité implicite
En connaissant le prix du marché d'une option, il est
possible d'obtenir une valeur unique pour la volatilité. Il suffit de
trouver la volatilité, notée crimp, telle que
l'estimation donnée par le modèle de Black-Scholes corresponde
à celle du marché. Cette valeur est appelée
volatilité implicite. Plus généralement, la
volatilité implicite d'une option est la volatilité permettant,
quand elle est injectée dans le modèle de Black-Scoles, de donner
le prix de l'option sur le marché.
26
La courbe de volatilité utilisée par les traders
pour évaluer les options sur devises a généralement la
forme d'un sourire, représenté dans la figure 3.1, d'où le
nom Smile. La volatilité est relativement faible pour des
options à la monnaie, et elle s'élève progressivement au
fur et à mesure que l'option devient davantage dans la monnaie ou en
dehors de la monnaie. On peut donc déterminer la distribution de
probabilité risque-neutre du prix d'un actif à
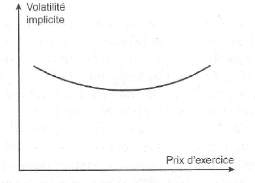
FIGURE 3.1 - Le smile de volatilité pour les options
sur devises, [14].
une date future T à partir du Smile
de volatilité déduit des prix d'options
d'échéance T. Cette loi est appelée distribution
implicite. Le Smile de volatilité de la figure 3.1 correspond
à la distribution de probabilité indiquée en gras dans la
figure 3.2. Une distribution log-normale avec la même moyenne et le
même écart-type est reportée en pointillé dans la
figure 3.2.
On peut voir que la distribution implicite a des
extrémités plus épaisses que celles de la loi
log-normale.
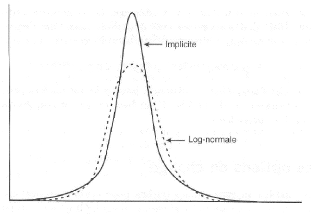
FIGURE 3.2 - La distribution implicite et la distribution
log-normale des taux de change, [14].
| 


