étude de l'efficience des marchés financiers. Cas de DZAIR index.

Chapitre III

Nous avons déjà trouvé dans l'analyse précédente de l'efficience faible du marché qu'il existe une autocorrélation de la série avec elle-même .

D'après le tableau, Il ne s'agit pas d'une marche au hasard (les coefficients de AC et PAC sont significatives) le processus est à mémoire, il existe donc une représentation dans la classe des processus ARMA.

Recherche des ordres p et q de la représentation ARMA :

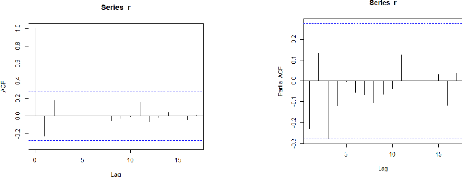
Pour déterminer l'ordre du retard de p et de q, nous avons présenté les corrélogrammes de la fonction d'autocorrélation simple et partiel

75

Compte tenu de la forme des corrélogrammes simple et partiel, max p=1 et max q =1 Nous sélectionnons donc un modèle ARMA (1, 1).

Le choix du meilleur model :

Le choix entre les trois model AR(1) et MA(1)Et ARMA (1 ,1) est par rapport à la critère AIC , c'est-à-dire le model le plus pertinent est celui qui a le minimum AIC

Et d'après le calcul dans le logiciel RStudio , nous avons choisir le model ARMA(1,1) :

76

Chapitre III

Tableau :

VARIABLE	coeficient	std.Error	t.Statistic
C	-0.0086	0.0079	-1.502
AR(1)	-0.7805	0.1911	-4.0839
MA(1)	0.5859	0.2375	2.4665

Min AIC -3.176889

Validation de la représentation

? Tests de Student sur les coefficients :

Les coefficients¹ sont tous significativement différents de 0 (probabilités critiques Inférieures à 0,05), sauf pour la constante avec une valeur de -0.0086 presque égale à 0. ? Analyse des résidus : (test d'homoscédasticité des résidus )

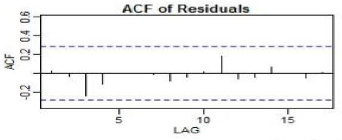
Le corrélogramme du résidu²indique qu'il s'agit d'un processus sans mémoire l'homoscédasticité des résidus est donc vérifiée. Les résidus sont donc un processus de bruit blanc.

La représentation est validée, la série de ROUIBA est un processus ARMA(1, 1)

¹ Test ARMA(1,1)

² Test de Box-pierce ou Ljung-Box effectué par RStudio

77

Chapitre III

Prévision :

Comme nous avons trouvé que la série est stationnaire et le test de l'homoscédasticité des

résidus est vérifié, donc nous pouvons faire des prévisions futurs sur la série de NCA-ROUIBA à travers le model choisi et estimé ARMA (1,1).

Le logiciel R va nous permettre directement d'effectuer cette opération de prévision en utilisant l'instruction suivante : sarima.for()¹

La prévision est pour 7 mois à partir de Juin 2019 jusqu'à décembre 2019 1) Les rendements futurs :

>sarima.for(rendement,n.ahead=7,p=1,d=0,q=1)

$pred

Time Series:

Start = 52

End = 58

Frequency = 1

[1] 0.003725608 -0.018144936 -0.001074932 -0.014398105 -0.003999341

[6] -0.012115598 -0.005780842

Le nombre d'observation : 52

Les résultats sont présentés au tableau

Le tableau des rendements prévus de ROUIBA

T	Ren dement (Rt)	?Rt
Juin 2019	0.37%
Juillet 2019	-1.81%	-2.18%
Aout 2019	-0.11%	1.70%
Septembre 2019	-1.44%	-1.33%
Octobre 2019	-0.40%	1.04%
Novembre 2019	-1.21%	-0.81%
Décembre 2019	-0.57%	0.64%

¹L'instructionsignifie : Forecasting with sarima model (voirl'annexe )