Chapitre III
Voici un résumé du test de dickey-Fuller :
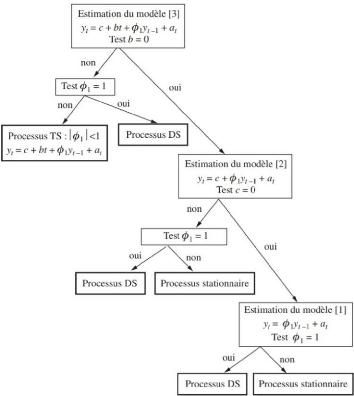
Schéma : les étapes du test de
dickey-Fuller1
72
1 BOURBONNAIS Econométrie
73
Chapitre III
d .Présentation de différentes formes des
séries temporelles :
Chart -1- Forme DS1 Chart -2- : forme TS 2
Chart-3- Forme TS et DS au même temps
1 DS :Differency Stationary 2TS
:Trend Stationary
74
Chapitre III
3 .Modèle ARMA :
Nous avons trouvés que toutes les séries de
l'indice DZAIRINDEX constituent un processus stationnaire, ce qui va nous
permettre d'essayer de faire des analyses et des prévisions selon le
model ARMA
a. Définition :
Les modèles ARMA sont représentatifs d'un processus
généré par une Combinaison des
valeurs passées et des erreurs passées.
b.Formulation
Pour un model ARMA(p, q) :
yt=u+O1xt-1+O2xt-2+...+Opxt-p+et-á1et-1-á2et-2
- ... -áqet-q
p et q sont le nombre de décalage dans le temps
c.conditions d'utilisation
Les modèles AR, MA, ARMA ne sont représentatifs que
de chroniques :
- stationnaires en tendance ;
- corrigées des variations saisonnières.
d.Cas empirique :
Nous allons étudier et analyser la série de
NC-ROUIBA et essayer de faire une prévision selon le model ARMA, tout en
suivant les démarches suivantes
Analyse des fonctions d'autocorrélation simple et
partielle sur la série stationnaire de ROUIBA :
Sample: 54(mois)
nombred'années: 5(ans)
|
AC
|
PAC
|
[1]
|
-0.23
|
-0.23
|
[2]
|
0.18
|
0.13
|
[3]
|
-0.33
|
-0.28
|
[4]
|
0.03
|
-0.12
|
[5]
|
-0.06
|
-0.01
|
[6]
|
0.05
|
-0.05
|
[7]
|
-0.03
|
-0.07
|
[8]
|
|
-0.06
|
-0.11
|
|
TABLEAU :d'autocorrélation simple et
partielle sur la série ROUIBA
| 


