étude de l'efficience des marchés financiers. Cas de DZAIR index.

Chapitre III

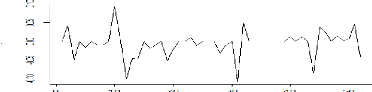
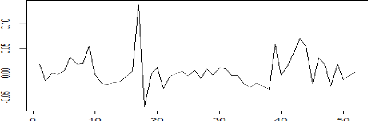
Figure 2 Représentation graphique de l'évolution des rendements des titres du DZAIRINDEX¹

Les tendances sont supprimées et les moyennes des séries semblent se situer sur une droite parallèle à l'axe des abscisses. Elles ne représentent presque pas de rupture sauf pour quelques titres comme 'BIOPHARM 'au début de 2016 car cette année représente l'année de son introduction en bourse (l'année de l'émission des titres), et aussi pour 'ROUIBA 'qui a connu une grosse dégradation à la fin du 2015 à cause de différent facteurs (économique, sociale, politique...)

Nous pouvons donc conclure à partir de cette représentation graphique que les courbes des rendements boursiers des titres du DZAIRINDEX ne suivent pas de tendance particulière, ni de saisonnalité, ce qui confirme donc que les séries sont stationnaires et qu'elles ne présentent aucune structure particulière. Nous allons néanmoins tester la stationnarité des séries afin de confirmer les résultats obtenus.

¹ Figures effectué par RStudio

70

Chapitre III

b. Test de Dickey-Fuller

Les tests de Dickey-Fuller (DF) permettent de mettre en évidence le caractère

stationnaire ou non d'une chronique par la détermination d'une tendance déterministe ou stochastique.

Les modèles servant de base à la construction de ces tests sont au nombre de trois. Le principe des tests est simple : si l'hypothèse H0 : (p1 = 1 est retenue dans l'un de ces trois modèles, le processus est alors non stationnaire.

[1] xt = (p1xt?1 + åt Modèle autorégressif d'ordre 1.

[2] xt = (p1xt?1 +c + åt Modèle autorégressif avec constante.

[3] xt = (p1xt?1 + bt + c + åt Modèle autorégressif avec tendance. Xt : variable testée

Xt-1 : variable testée en tenant compte de ses conditions du passé c : constantes

bt : tendance

åt : terme d'erreur

Les hypothése du test :

H0 : (p1 = 1 indique la non stationnarité H1 : |(p1| < 1indique la stationnarité Dans le dernier modèle [3] :

Si t(p1>ttabulé, alors on accepte l'hypothèse H0 ; il existe une racine unité, le processus n'est donc passtationnaire.

Et si t(p1<ttabulé, et si le coeficient b est significativement différent de 0 alors le processus est stationnaire

Nous avons donc appliqué le test de Dickey-Fuller augmenté (ADF) Sur RStudio, pour toutes les séries de rendements .

71

Chapitre III

TableauRésultat du test de Dickey-Fuller ¹augmenté (ADF)

Titre	t Statistique	Valeurs critiques à 5%	Resultat du test
BIOPHARM	-5.8514	-3.5	a1
SAIDAL	-4.2665	-3.45	a1
ROUIBA	-4.7726	-3.45	a1
AURASSI	-4.8254	-3.45	a1
ALLIANCE	-6.4961	-3.5	a1
AOM	-6.6221	-3.6	a1
DZAIRINDEX	-4.6102	-3.45	a1

Interprétation économétrique :

Pour ce qui est de la stationnarité des séries, le tableau, présente auparavant, nous indique que les rentabilités boursières, objet de notre étude, montrent une certaine stationnarité. En effet, toutes les valeurs de t-statistique, sans exception, sont significatives à moins de 5%.

T calculé(t statistique) < T tabulé (valeur critique à 5%) , ce qui veut dire que l?hypothése H1 est accéptée ( |ö1| < 1 ) .

Les tendances sont ainsi supprimées², et les rentabilités se situent sur une droite parallèle à l'axe des abscisses , L'hypothèse de stationnarité est donc vérifiée.

¹ Calcule effectué par RStudio

²Au cas de non supréssion de la tendance la série est TS (trend stationnary)