Une description de differentes options exotiques à partir du modèle de Cox Ross et Rubinstein sur quelques periodes

2 L'option asset or nothing

Définition 6. L'option asset or nothing permet de toucher la valeur dusous acent ST à la date T , lorsque l'option est exercée.

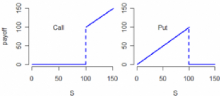
FIG. 3 - Exemple du payoff asset or nothing K=100T=1 an

2.1 Exemple

On reprend toujours les mêmes données mais cette fois le payoff vaut le sous jacentt

On a sous forme d'arbre Casset

0 = 21, 754

At each node:

Upper value = Underlying Asset Price Lower value = Option Price

Values in red are a result of early exercise.

Strike price = 50	1,0042
Discount factor per step = 0,9958
Time step, dt = 0,0833 years, 30,42 days
Growth factor per step, a = 1,0042		79,353
Probability of up move, p = 0,4892		79,354
Up step size, u = 1,1224	70,699
Down step size, d = 0,8909	64,12
62,989		62,989

0

31,505

0

50

21,754

44,547

32,957

11,202

56,12

47,509

39,689

3,5481

19,289

50

44,547

31,989

35,361

56,12

7,283

50,053

39,689

14,95

50

0

99,967

99,967

89,066

89,066

79,353

79,353

70,699

70,7

62,989

62,989

56,12

30,687

50

0

44,547

0

39,689

0

35,361

0

31,505

0

28,069

0

25,008

0

Node Time:

0,0000 0,0833 0,1667 0,2500 0,3333 0,41 67 0,5000

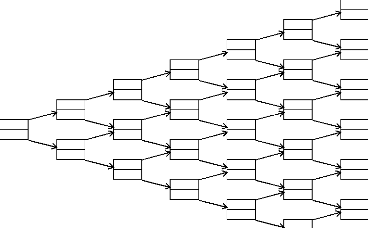
FIG. 4 - Evaluation du call asset or nothing dans l'arbre binomial

2.2 Expression mathématique

De façon mathématique on peut exprimer le call d'une option asset or nothing à ladate T comme :

? ????????? ? ??????????

ST si ST > K 0 sinon Ou encore ST1ST=K

Pour exercer ce call il faut que le sous jacent dépasse le seuil K à la date T. De la même manière que pour le call cash or nothing le nombre minimal de hausses pour que la valeur du cours du sous jacent dépasse K est égal à

h0 = 1+ rn(S(dKn)l

ln(Uⁿ_n:)

On peut donc donner le prix du call asset or nothing à la date initiale.

Proposition 7. Le prix d'un call binaire asset or nothing dans lele modèle CRR à a date d'aujourd'hui est

C0 = S.P⁰(ST > K)

où P⁰ est une nouvelle probabilité

preuve : Le prix d'un call à la date t = 0 est l'espérance actualisée au taux sans risque

du payoff de l'option. Soit

[ST¹ST=K}]

(1 + r_n)ⁿ

On partage la durée de vie de l'option en n périodes on peut alors écrire que

donc	[ST^1ST=K}]	= S	Xn h=h0	~npnun h (0-^pn) dn)n h h) 1+rn 1+ rn 27
	(1 + rn)^n

P (ST > K) =

X (nh)pnh(1

n

h=h0

On pose alors

p' n = pnunet 1 - p' n ₌(1 - p_n) d_n 1 + r_n1 + r_n

Et on obtient

EP [ST1ST=K] = S

Xn(n ) ((pn)^'h(1 - p^' n) ^n-h= SP^' (ST > K) h h=h0

2.3 Convergence du modèle de Cox Ross et Rubinstein

Tout comme dans l'option cash or nothing, on va chercherla valeur de P^' (ST > K) en divisant la période de vie de l'option en très petites périodes de longueur A_n de sorte à faire converger la loi binomiale vers une loi normaleLes calculssont les mêmes mais la probabilité diffère. Sous les mêmes conditions queloption cash or nothing nous allons devoir calculer P^' (ST = K)

Proposition 8. La probabilité d'exercer un call binaire asset or nothing estP^' (ST = K) = N (a1) où N est la fonction de répartition de la loi normale centrée reduite.

preuve : De la mème manière que pour le call cash or nothing nous allons avoir besoin de calculer :

lim n?+8	h0 - np' n	=lim n?+8	ln(K ) +nóvÄn(1 - 2p^' n) S
	/ n (p'n(1 - p'n))		/ 2ó Änn (p'n(1 - p'n))

en utilisant les developpements limités e^x 1 + x +x2 2 pour x proche de zero et le fait que

nÄ_n = T on montre :

'

puisque p_n = erÄn

n

1 1

' ( ó2 )

+ r + 'VA_n

p_n R-''' 2 2ó 2

1 -- 2pn R-''' --

ó) 2 1 r + An ó ( 2

On en déduit d'une part que ::

lim n,+cc		2ó'VÄnn (p'n(1 --p'n)) = lim 2ó \lÄnn (^1) = óN/T n,+cc 4
d'autre part :	lim n,+cc		n (1 -- 2p^'n) 'V An = --T (^ó2 +^ór )

ce qui nous donne :

lim n,+cc		h 0 -- np^'n		ln (P -- T (52 + ró;)	lnG^sj+T(`;+^ró;) ó N/T	= --a1
	'Vn (p'n(1 -- p'n))			óN/T

On peut alors réécrire la probabilité suivante en notant X^'_n la loi binomiale de paramètre

'

n , p_n :

( X_n -- np^' h0 -- np^'_n )

P(X:., > h0) = P n >

'Vn (p'_n(1 -- p'n)) -- 'Vn (1n(¹ -- p'n))

et donc

1

P(X^'_n > h0) = P (AT (0,1) > --a1) = N/2ð

lim

x,+cc

-y² 1

e ² dy =

2

y , , _r

e ² ay = JV (a1)

+cc

_f

-a1

a1

_f

-cc

N/2ð

où AT est la fonction de répartition de la loi normale centrée réduite

Application à l'exemple On reprend les données de l'exemple. On calcule alors a1 = 0, 2298 Le calcul donne : V (a1) = 0, 5908. On multiplie alors par la valeur du sous jacent à l'origine et on obtient :

C

asset 0 = 50.0, 5908 = 29, 544
Le problème du nombre de périodes insuffisant est toujours le même.