Programmation des robots industriel et application sur le robot manipulateur Algérie machines outil 1

3.2 Les erreurs statique et dynamique

3.2.1 Les erreurs de positionnement d'un manipulateur [55, 65] :

Le positionnement réel d'un manipulateur, que ce soit en statique ou en dynamique (poursuit des trajectoires) s'écarte inévitablement et pour différentes causes, de sa position désirée. De même, un manipulateur ne se positionne jamais au même endroit lorsque la même trajectoire est répétée plusieurs fois ».

Ces erreurs de positionnement sont d'origines diverses, peuvent être classées en quatre catégories principales :

- Erreurs de quantification et de calcul.

- Erreurs cinématique de type aléatoire dominant.

- Erreurs d'étalonnage et d'identification.

- Erreurs cinématique de type systématique dominant.

Les erreurs de quantification et de calcul :

sont liées à :

- L'arrondi dans les calculs effectués par le calculateur.

- La quantification des codeurs incrémentaux ou absolus utilisés pour la détermination des coordonnées articulaires.

- La performance du calcul numérique et des algorithmes employés.

- La troncature des valeurs numériques dans les calculs trigonométriques

Les erreurs cinématique de type aléatoire dominant:

Chacune des articulations d'un manipulateur à motorisation électrique peut être déplacée à l'intérieur d'une petite zone, sans entraîner de signale d'erreur à l'intérieur du système d'asservissement. Cette zone morte est due aux défauts géométriques non systématiques des organes mécaniques (les jeux mécaniques) à la résolution des capteurs et aux performances des asservissements (non linéarités dues aux frottements mécaniques par exemple) [10, 65].

Les erreurs cinématiques de types systématique dominante sont liées à :

- La déformation des segments sous l'effet des charges statiques et dynamiques.

- La déformation des articulations sous l'effet des charges statiques et dynamique. - La dilatation des pièces mécaniques de la structure sous l'effet de la température.

3.2.2 Identification des paramètres d'un manipulation :

L'identification consiste à déterminer, suite à une série de mesures et à l'aide des méthodes de masse du manipulateur [55,66].

Les erreurs de positionnement statique d'un manipulateur sont de deux natures : Géométrique et non géométrique.

Les erreurs géométriques : Elles regroupent les imprécisions de fabrication dons les corps et les liaisons et les erreurs d'initialisations des offsets codeurs (les valeurs des offsets codeurs correspondants à la configuration initiale géométrique dans laquelle les variables articulaires sont nulles).

Les erreurs non géométriques : Elles regroupent les déformations, les jeux dans les chaînes cinématiques, les erreurs liées à la résolution des capteurs et aux performances des asservissements. Elles ne sont pas accessibles à la calibration géométrique.

La procédure d'identification géométrique distingue trois niveaux de complexité :

Niveaux 1 : Ou « calibration des articulations », l'objectif est d'établir la relation la plus exacte entre le signal produit par les capteurs de position et les déplacements articulaires. Ceci, implique généralement la calibration de la cinématique des organes d'entraînement (réducteurs, courroies, .etc.), les mécanismes des valeurs des offsets codeurs.

Niveaux 2 : Ou « calibration géométrique globale » dans ce niveau on doit identifier tous les paramètres géométriques de description du manipulateur. L'objectif de ce niveau est de déterminer le modèle géométrique de base, qui lie les coordonnées opérationnelles aux coordonnées articulaires (ou valeurs de commande des actionneurs).

Niveaux 3 : Ou « calibration non géométrique », il porte sur les possibilités de compenser les erreurs d'ordre non géométriques à savoir les déformations des articulations et des segments et des frottements.

Pour utiliser le modèle dynamique, il faut connaître les valeurs numériques des paramètres de masse (masse, centre de masse, et matrice d'inertie) relatifs aux différents corps et qui interviennent dans le modèle dynamique. Plusieurs techniques peuvent être envisagées pour estimer ces paramètres : Soit par calcul au moment de la conception, surtout si on utilise un logiciel de C.A.O. performant, soit par mesure corps par corps avant le montage ou par identification.

La technique d'identification des paramètres, consiste à exploiter le caractère linéaire des actions dynamiques relativement à ces paramètres pour les identifier, en utilisant la méthode d'optimisation des moindres carrée[56] .

La précision d'un manipulateur est généralement définie en terme de précision statique (les caractéristiques de pose) et de précision dynamique (les caractéristiques de trajectoire), ces deux caractéristiques, quantifient la différence entre la situation désirée et celle réellement atteinte [10, 65, 67].

Pour les manipulateurs utilisés dans les tâches d'assemblages, d'insertion de composants, de soudage par point..., les caractéristiques de composantes sont les caractéristiques de pose. Ces caractéristiques sont définies par trois termes:

- Exactitude statique.

- Répétitivité statique.

- Temps de stabilité et dépassement statique.

Selon la définition ISO, l'exactitude statique est représentée par l'écart entre une pose commandée (P_c) et la moyenne des poses réellement atteintes (figures 3.1) , lorsqu'on demande au manipulateur de se positionner plusieurs fois en P_c en suivant toujours la même trajectoire (exactitude statique unidirectionnelle) soit P_c le point de la position commandée de coordonnées X_c , Y_c , Z_c dans le référentiel de bas {R_o}; Pi une des positions réellement atteintes (i= 1, k) , P_c = [ X_c , Y_c , Zj

et Pi = [Xi , Yi , Zi]^T

Pi

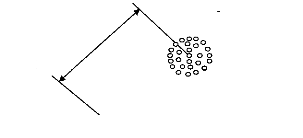
Les positions atteintes

P_c

La position programmées

Figure 3.1: L'exactitude de positionnement statique d'un manipulateur [55].

L'exactitude locale de position E_s est la distance entre le point P_c et le point P_g barycentre de tous les points atteints Pi donc:

E s ( x

=

g xc)² ( y _g y c ) ² ( z g z c )2

- + - + -

(3.19)

? y_i

=1 ; i = = 1

i =

Y g = 1 ; k

Z g

k k

avec: X_g i

? xi

? zi

i k

=	i k =i k =

Pour les rotations, on peut définir de la même manière la variation entre la moyenne des positions angulaires atteintes et la valeur commandée.

Par définition la répétitivité statique unidirectionnelle est la distance maximale entre le point moyen P_g et les points réellement atteints Pi , i= 1 .k (Figure 3.2)

P_g

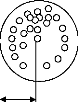
Pi

Les positions atteintes. R_s

Figure 3.2: La répétitivité de positionnent statique d'un manipulateur [55].

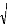
R Max 1 x x y y z z

= = - + - + -

( ) ² ( ) ² ( )² .. (3.20)

s i k k i k i k i

La norme (NF-E 61-103) définit également une répétitivité statique à partir de la moyenne de distances entre P_g et les points atteints Pi.

Si les trajectoires pour atteindre la position désirée P_c sont différentes (on partira de différentes positions vers la même destination). L'exactitude et la répétitivité vont avoir des valeurs différentes appelées exactitudes et répétitivité multidirectionnelles.

Dans le cas où la position commandée serait définie par apprentissage, la répétitivité est la même, par contre l'exactitude est très différente, pour les manipulateurs très précis la répétitivité peut être de l'ordre du centième de mm, alors que l'exactitude de position programmée peut être de plusieurs mm.

Remarque: Au terme répétitivité on associe souvent la notion de réversibilité qui caractérise la précision statique quant le point est atteint selon plusieurs directions ; elle est plus mauvaise que la répétitivité.

Il est bien intéressant de connaître le comportement du robot lorsqu'il approche une pose commandée. Suivant le réglage des asservissements des actionneurs et le niveau de déformations des segments, le manipulateur peut osciller, dépasser la situation commandée ou au contraire s'en approcher sans oscillation, ce comportement se traduit par deux caractéristiques : Dépassement et temps de stabilisation ces caractéristiques peuvent être utiles pour régler une temporisation du manipulateur avant d'effectuer une tâche ; la

connaissance du dépassement permet de s'assurer que l'espace dégagé autour du point d'arrêt est suffisant pour éviter les collisions de l'outil avec l'environnement [65].

En robotique, de nombreuses tâches sont réalisées en utilisant un mode de commande de type interpolation linéaire ou circulaire afin de quantifier les défauts et les écarts entre la trajectoire réellement parcourue et la trajectoire commandée, les caractéristiques essentielles pour ces applications sont définies par les notions d'exactitudes et de répétitivité de trajectoire.

Elle caractérise l'aptitude d'un manipulateur à faire suivre à l'interface mécanique (l'effecteur) une trajectoire désirée le fois dans la même direction et le fois dans la direction opposée [10].

L'exactitude de trajectoire est définie par la distance maximale entre la ligne moyenne des trajectoires réellement atteintes et la ligne programmée (Figure 3.3), mesurée dans un plan orthogonal à la trajectoire.

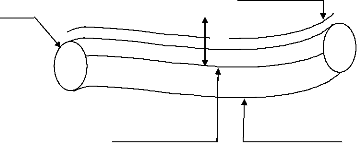
Et

R+

La ligne moyenne des trajectoires effectuées

Enveloppe des trajectoires effectuées

Trajectoire programmée

Figure 3.3: Exactitude de trajectoire [55]

L'exactitude pour des positions ou des trajectoires programmées dépend surtout d_s erreurs d'étalonnage et des erreurs dues aux déformations de la structures mécanique du manipulateur [10, 65, 70].

La répétitivité de trajectoire (ou dynamique) est la distance moyenne (ligne des barycentres des trajectoires effectuées) et une trajectoire effectuée; sera donc le rayon du tore qui contiendrait toutes les trajectoires effectuées (Figure 3.3).

Les erreurs de répétitivité sont dues aux défauts géométriques non systématiques des organes mécaniques, à la résolution des codeurs de positions et aux performances des asservissements (non linéarités dues aux frottements mécaniques par exemple)

[10, 65] avec le développement de l'électronique, de l'informatique et des moyens de fabrication (machine à commande numérique, CFAO) la précision géométrique en terme de répétitivité tend à devenir largement suffisant pour la majorité des applications industrielles.

Les applications industrielles de la robotique font appel à des modes d'emploi principaux des manipulateurs:

De point d'arrêt acquis par apprentissage d'une suite discrète de configuration articulaires.

- De trajectoires acquises par l'enregistrement échantillonné d'une suite continue de configurations articulaires correspondants aux mouvements que doit reproduire le manipulateur.

Les points d'arrêt sont seuls fonctionnels (travail en cours mouvement).

Dans ces quatre types d'emploi, le problème de précision prend des dimensions tout à fait différentes:

- Il peut dépendre de la répétitivité de la réversibilité, de l'exactitude statique ou dynamique (§ 3.3) ou de l'un de ces critères seulement.

Les déformations de la structure mécanique peuvent être tout à fait transparentes à l'utilisateur comme elles peuvent s'imposer comme un aspect du comportement dont la modélisation et la prise en charge est vital pour l'application.