Programmation des robots industriel et application sur le robot manipulateur Algérie machines outil 1

CHAPITRE 3
LES CAUSES STRUCTURELLES

3.1 Modèles dynamiques des systèmes mécaniques poly articules aux joints déformables

3.1.1 Descriptions d'une liaison déformable : [47, 48, 49] :

Nous supposons que la déformation du joint est supposée localisée à la sortie réductrice. Pour chaque articulation nous prendrons deux variables articulaires _q2i-1 ^et _q2i ou :

Q2i-1 : Variable articulaire délivrée par l'actionneur;

Q2i : Variable articulaire prise par le segment ;

3.1.2 Hypothèses du travail:

- Les segments sont supposés parfaitement rigides;

- Les liaisons sont prismatiques ou rotoides élastiques linéaires;

- La dissipation d'énergie dans les liaisons est du type visqueux.

3.1.3 Mise en équation : [49, 50, 51, 52, 53, 54] :

Pour la mise en équation du modèle dynamique nous avons utilisées le formalisme de Lagrange associé à la méthode Uiker (même démarche que dans le chapitre 2), ce qui conduit au calcul de:

L'énergie de dissipation par frottement visqueux dans le joints EP=Ep (q2i-1 ,q2i). 3.1.4 Energie cinétique, potentiel et de dissipation du système :

Pour un système mécanique articulé à joints flexibles, l'énergie cinétique est calculée en considérant ; la structure comme une chaîne ouverte simple à 2n éléments les n segments et les n actionneurs qu'on peut mettre sous la forme quadratique suivante :

1 2 [ ] 2 2 2 1 [ ] 2 1

1

E q A q q I q

c i

= + - -

& & & &

t ^t ... (3.1)

i i a i

2

[A] : Représente la matrice de masse relative aux coordonnées généralisées q2i.dimension (n*n) symétrique définie positive.

41 [I_a] : Matrice des inerties des actionneurs de dimension (n*n) diagonal, construite par les éléments de type 2

N_i I_a tel que:

N_i: Rapport de transmission du i^éme actionneur N_i = 1

Ia : Inertie du rotor et du premier étage du réducteur du i^éme actionneur.

Q2i : Vitesse généralisée relative au i^éme segment .

Q2i-1: Vitesse généralisée relative au i^éme segment.

L'énergie potentielle est calculée de la même façon que dans le cas rigide, mais tout considérons la structure comme une chaîne cinétique simple à 2n éléments, les n segments et les n actionneurs :

E_p =E_p (ext)+E_p (int) (3.2)

Avec E_p(ext)=E_p (pesanteur).

Ep(int)= Ep (élastique).

L'énergie potentielle s'écrit sous la forme :

n Epint = ? i 1 =

Epi ( q2i-1-q2i) . (3.3)

n

Epint = ?=

i 1

1 Ki ( q2i-1-q2i)² . (3.4)

2

En posant:

EPint = ?i = q2i-1-q2i .(3.5)

n

EPint = ?=

i 1

1 Ki (?i)² . (3.6)

2

ED=?= i 1

ED (

. q2i-1 ,

. q2i-1 ) (3.9)

Ki: Représente la constante de rigidité du i^eme joint élastique.

?i: Représente le déplacement angulaire relatif au niveau du i^éme joint :

EPint = 1 {? }T [ T] {? } ....(3.7)

2

{? } : Matrice uni colonne des déplacements angulaires.

[K] : Matrice de rigidité des joints de dimension (n*n).diagonale :

n

EPext = Epg =? i 1 =

Epg ( q2i) .(3.8)

C'est une forme quadratique des vitesses angulaires relatives aux joints, on aura:

n

n

ED=?₌

i 1

. .

1 bi ( _q2i-1 , _q2i ) ² (3.10)

2

n

ED = ?=

i 1

1 .

bi (?)² (3.11)

2

. .

ED = 1 { ? }^T [D] {? } (3.12)

2

{? }: Matrice uni colonne constituée des vitesses angulaires.

[D]: Matrice des coefficients d'amortissement dimension (n*n) diagonale.

Si nous appliquons le principe des puissances virtuelles et le formalisme de Lagrange conduisent aux 2n équations suivantes:

+j j = 1,2 .n (3.13)

Ki( q2i-q2i-1)-bi( q2i-q2i-1) = i si i = 2i-1

+Ki( q2i-q2i-1)-bi( 2qi-q2i-1) = 0 si j = 2i (3.14)

? E p
? q j

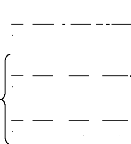
? E c =

?E_D

?

?

?

??

d

.

? q

j

?Epg

+

? q i

?Epg

+

?q_i

? E c

?

?

?

??

? q j

? q j

dt

d ? ? E ?

c

dt ?? q ??

? i

d ??E?

c

dt ?? q ??

? i

-

-

?E c

?q_i

?q i

?E c

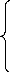
On posant la variable articulaire [q]= telle que : [qi]=[q2i-1] et [q2]=[q2i] i=1,n.

On aura le système d'équation suivant :

.. .

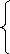
[A] q1+[B] q1

..

. . .

q1+[C] ²

q& 1 - G + [K] ( q1-q2) +[D] (q1-q 2) = 0

(3.15)

. .

[I_a] q2 - [K] (q1-q2) -[D] (q1 - q2) =

[A] : Matrice de masse.

[B] : Matrice de Coriolis.

G : Matrice uni colonne des termes de gravité.

Si le système mécanique est à joints parfaitement rigides. Le coefficient de rigidité K -) 8

B -) 0 , q1-) q2 et q1-q2-) 0.

Le système d'équation devient alors :

.. [As] q1+[B]		. q1	. q1+[C] ^2 q& i - G = 0
[Ia]	.. q1 =			(3.16)

Tel que [A_s] est la matrice d'inertie de la partie segments et [I_a] est la matrice d'inertie de la partie actionneurs.

Si on additionne membre à membre les équations (1) et (2) on retrouve les équations du système poly articulés indéformables données sous la forme matricielle suivante :

.. . . .

=[A] q+[B] q.q +[C] q² - G Sachant que [A]=[AS]+[I_a].

3.1.5 Résolution des équations: [4 , 49, 68, 69] :

Pour la résolution du système d'équations on utilise la méthode de Runge - Kutta à quatre approximations pour cela on arrange le système comme suit :

.. . . . .

q1 = - [Aï¹ [B] q1q1+[C] ²

0

0

q& _i - G + [K] ( q1-q2) +[D] (q1 - q2)

..

. .

q2 = [I_aï¹ [ + [K] ( q1-q2) +[D] (q1 - q 2)]

(3.17)

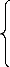
Les conditions initiales sont :

q1	( ) 0 ( ) 0 t = q q & t = q & 0 1 1 0 1

q t = q q & t = q &

2 0 2 2 0 2

( ) ₀ ( ) 0

on pose

[Y] =

q1 q2 q2 q2

? ? ? ? ? ?

Et donc nous avons :

d= dt

q1 . q1 q2 . q2

? ? ? ? ? ? ??

? ? ? ? ? ?

&

2

G+

-

1

&

q₁

[ ] [ ] , [ ]

A q B q q C q

- 1 & & & &

1 1 2

+ +

[ ] ( ) [ ] ( )

K q q D q q

- + -

& &

1 2 1 2

)]

?

?

?

?

?

??

.(3.18)

d Y

[ ]

=

dt

&

q₂

K q q D q q

& &

1 2 1 2

I a

[ ] [ [] ( ) [ ] (

- 1 + - + -

q₁

&

q₁

q₂

q₂

d

dt

Qu'on peut poser sous la forme suivante :

d [Y] = É (t , [Y] ) dt

Sachant que [Y(t0)] = [Y0] on obtient le système d'équation différentielle suivant :

d [Y] = É (t , [Y] ) dt

[Y] = [Y0] pour t = t0

Qu'on peut résoudre par la méthode de Runge -Kutta .