Applications des intégrales stochastiques en macroéconométrie

4.2.4 Résultats des estimations

Nous avons utilisé l'indice des prix à la consommation (IPC) calculé par la Banque Centrale du Congo observé à Kinshasa pour la période allant de janvier 2004 à avril 2016. Pour obtenir l'inflation,nous avons transformé cette variable en log-différentiel,i.e,

tt =A (log(IPC)t) = logYt - logYt_1. Pour le modèle AR(1), les résultats se présentent comme suit

àðt = 0, 54irt_1, T = 146,

t - Student = 7,71, DW = 2, 19,

où T représente la taille de l'échantillon, t - Student est la statistique de Student pour tester la significativité des paramètres estimés et DW représente la statistique de Durbin et Watson pour tester l'absence d'auto-corrélation des erreurs du modèle estimé.

t t

Après l'estimation de notre modèle AR(1), l'équation intégrale stochastique de l'inflation de Kinshasa se présente comme suit

_{Z Z}

àðt = ir0 + 0, 46 ₀ ir_sds + 0, 02 ₀ dBs.

Comme la statistique de t-student du coefficient estimé est supérieure à 2, en valeur absolue ,selon la règle de pouce,nous pouvons conclure que ce paramètre estimé t9 à est significatif,c'est- à -dire,ce paramètre est statistiquement différent de zéro. Aussi comme la valeur estimée de la statistique de Durbin - Watson est au tour de 2, nous concluons qu'il y a absence d'autocorré-lation des erreurs dans le modèle AR(1) estimé. La valeur de la volatilité stochastique est de 0,02 qui montre sous la période sous analyse une faible présence d'incertitude. La persistance à la hausse de l'inflation de Kinshasa est de 54%,c'est-à -dire,l'inflation du mois passé contribue de 54% à l'inflation présente .

4.3 Estimation de la contribution stochastique de la main d'oeuvre congolais sur son bien - être économique

Connaitre les contributions de différentes variables explicatives du développement économique de sa population est une préoccupation majeure de tout décideur ou le planificateur du développement économique. Le filtre de Kalman - Bucy est reconnu comme l'une des techniques couramment utilisées dans les domaines de navigation, contrôle, de lancement de missiles et navettes spatiales, analyse de processus de signaux médicaux, etc. ([77],[53],[46],[103],[81],[? ],[161],[13],[129],[131]). La portée de cette technique ne s'est pas limitée uniquement dans ces domaines mais aussi elle est utilisée en macroéconométrie pour estimer les composantes non observables stochastiques des agrégats macroéconomiques ([73], [75], [76],[74] ).

4.3.1 Modèle théorique du bien - être économique

L'analyse théorique des effets des facteurs de production (travail, capital et la technologique) est plus ancienne et constitue la préoccupation des économistes théoriciens et des décideurs politiques en charge de la bonne conduite de la politique économique du pays.

Nous supposons que la fonction de production de bien

4.3.2 Spécification économétrique du modèle état - espace du développement économique

Nous supposons que le modèle d'état - espace du bien - être congolais se présente comme suit :

le processus d'observation

gt = ^à131,txt +

^à132,tyt +

^ài3,tZt + [var = exp(

^àe1)]

avec les processus stochastiques non observés d'états suivants

^àâ1,t =	^à/1,t-1 + [var = exp(	^àe2)],
^àâ2,t =	^àe4 + à/32,t-1 + [var = exp(^àe3)],

66

^à/33,t = ^àe5 + ^à/33,t-1,

à

où _/3j,t mesurent les effets de ces trois différents facteurs de bien - être congolaise au temps t et ^àBi sont les paramètres constants du modèle état - espace stochastique.

Les hypothèses du modèle sont (i) les séquences vt et _Ek,t sont des bruits Gaussiens,(ii) les coefficients sont des processus stochastiques et variants avec le temps.

4.3.3 Estimation du modèle de bien - être congolais

Il y a deux avantages de présenter un système dynamique dans le modèle d'état - espace : (i) le modèle d'état espace permet aux variables non observables (variables d'état) d'être incorporées et estimées dans le modèle observé, (ii) les modèles d'état espace peuvent être analysés en utilisant l'algorithme récursif puissant comme le filtre de Kalman et Bucy [99] et [100], (iii) E[vtEk,t] = 0, .

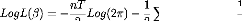
Pour implémenter le filtre de Kalman, nous appliquons la fonction de maximum de vraisemblance suivante

2 Log(2r) - 2 Log

Ft(B)

1

|

|-

2 ~-1

t (è)~t(è).

t t

Cette fonction peut être évaluée en utilisant le filtre de Kalman. En utilisant les dérivées numériques, les techniques itératives standards peuvent être employées pour maximiser la fonction de maximum de vraisemblance des paramètres inconnus. Dans cette étude la technique itérative utilisée est celle de Berndt, Hall,Hall et Hausman [? ].

L'algorithme de BHHH [? ] est une méthode numérique similaire à celle de Gauss - Newton. Elle se présente comme suit. Supposons que la fonction à optimiser est Q(/3). Alors les algorithmes sont itératifs définissant une suite d'approximation, /3k, donnée par

?Q

/3k+1 = /3k - ëkAk a/3 (/3k)

où /3k est le paramètre à estimer à l'étape k, et Ak est une paramètre appelé la taille de l'étape qui partiellement détermine l'algorithme particulier. Pour l'algorithme BHHH de Ak par les calculs avec une étape donnée est déterminé L 'Algorithme de Kalman que nous avons utilisé peut être résumé comme suit

LogL(/3) = -

nT

67

68

(Leondes,p.241). Le modèle dynamique se présente comme suit

Xk = Ok-1Xk-1 + Wk-1, Wk-1 ^' N(0, Qk-1)

et l'équation de l'état se présente

Zt = HkXk + vk, vk ^' N(0, Rk)

les conditions initiales sont

E(X0) =

^àX0|0,

E(X0 -

^àX0|0)(X0 - ^àX0|0) = P0|0, E(Wkv⁰_j) = 0 pour tous k et j.

^àXk|k-1 = Ok-1^àXk-1|k-1

La matrice de covariance des erreurs de propagation est donnée par

Pk|k-1 = Ok-1Pk-1|k-1(P⁰k-1 + Qk-1

Le vecteur état

[ ]

^àXk|k = ^àXk|k-1 + Kk Zk - H ^àXk|k-1

Matrice de covariance des erreurs est donnée [ ] Pk|k-1 = I - KkHk Pk|k-1 La matrice de gain de Kalman est donnée par Kk = Pk|k-114 [HkPk|k-1H ^0k + Rk]

-1

4.3.4 Présentation et Interprétation des résultats

Les résultats de cette étude sont présentés dans le tableau suivant :

69

Paramètres du modèle valeurs estimées

^àè1 -3,3867^*

^àè2 -16, 2692

^àè3 -6, 4230

^àè4 1,2807

^àè5 -0, 0081^**

Etats du modèle valeurs estimées

^àâ1 -0,3634^**

^àâ2 49, 6594^*

^àâ3 0, 2352

(*) et (**) sont respectivement significatifs au seuil de 5% et 10%.

Comme indiqué dans le tableau ci - dessus, la significativité des paramètres de ce modèle est déterminée par la valeur de Z - statistique associée à chaque paramètre. La lecture de ce tableau montre que les coefficients de variables investissements et populations sont significatifs.

Eu égard à ces estimations, la population active congolaise ont des effets positifs sur la croissance économique. Par contre, les investissements ont des

effets négatifs sur la croissance économique.